|
Spatial Gradient
A spatial gradient is a gradient whose components are spatial derivatives, i.e., rate of change of a given scalar physical quantity with respect to the position coordinates in physical space. Homogeneous regions have spatial gradient vector norm equal to zero. When evaluated over vertical position (altitude or depth), it is called ''vertical derivative'' or ''vertical gradient''; the remainder is called ''horizontal gradient'' component, the vector projection of the full gradient onto the horizontal plane. Examples: ;Biology * Concentration gradient, the ratio of solute concentration between two adjoining regions * Potential gradient, the difference in electric charge between two adjoining regions ;Fluid dynamics and earth science * Density gradient * Pressure gradient * Temperature gradient ** Geothermal gradient ** Sound speed gradient * Wind gradient * Lapse rate See also *Grade (slope) *Image gradient *Time derivative *Material derivative *Structure tensor In m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of f. If the gradient of a function is non-zero at a point p, the direction of the gradient is the direction in which the function increases most quickly from p, and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function f(\mathbf) may be defined by: df=\nabla f \cdot d\mathbf where df is the total infinitesimal change in f for a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Density Gradient
Density gradient is a spatial variation in density over a region. The term is used in the natural sciences to describe varying density of matter, but can apply to any quantity whose density can be measured. Aerodynamics In the study of supersonic flight, Schlieren photography observes the density gradient of air as it interacts with aircraft. Also in the field of Computational Fluid Dynamics, Density gradient is used to observe the acoustic waves, shock waves or expansion waves in the flow field. Water A steep density gradient in a body of water can have the effect of trapping energy and preventing convection, such a gradient is employed in solar ponds. In the case of salt water, sharp gradients can lead to stratification of different concentrations of salinity. This is called a Halocline. Biology In the life sciences, a special technique called density gradient separation is used for isolating and purifying cells, viruses and subcellular particles. Variations of this inc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Structure Tensor
In mathematics, the structure tensor, also referred to as the second-moment matrix, is a matrix (mathematics), matrix derived from the gradient of a function (mathematics), function. It describes the distribution of the gradient in a specified neighborhood around a point and makes the information invariant to the observing coordinates. The structure tensor is often used in image processing and computer vision. J. Bigun and G. Granlund (1986), ''Optimal Orientation Detection of Linear Symmetry''. Tech. Report LiTH-ISY-I-0828, Computer Vision Laboratory, Linkoping University, Sweden 1986; Thesis Report, Linkoping studies in science and technology No. 85, 1986. The 2D structure tensor Continuous version For a function I of two variables , the structure tensor is the 2×2 matrix S_w(p) = \begin \int w(r) (I_x(p-r))^2\,dr & \int w(r) I_x(p-r)I_y(p-r)\,dr \\[10pt] \int w(r) I_x(p-r)I_y(p-r)\,dr & \int w(r) (I_y(p-r))^2\,dr \end where I_x and I_y are the partial derivatives of I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Material Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In this case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Time Derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t. Notation A variety of notations are used to denote the time derivative. In addition to the normal ( Leibniz's) notation, :\frac A very common short-hand notation used, especially in physics, is the 'over-dot'. I.E. :\dot (This is called Newton's notation) Higher time derivatives are also used: the second derivative with respect to time is written as :\frac with the corresponding shorthand of \ddot. As a generalization, the time derivative of a vector, say: : \mathbf v = \left v_1,\ v_2,\ v_3, \ldots \right is defined as the vector whose components are the derivatives of the components of the original vector. That is, : \frac = \left \frac,\frac ,\frac , \ldots \right . Use in physics Time derivatives are a key concept in physics. For example, for a changing position x, its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Image Gradient
An image gradient is a directional change in the intensity or color in an image. The gradient of the image is one of the fundamental building blocks in image processing. For example, the Canny edge detector uses image gradient for edge detection. In graphics software for digital image editing, the term gradient or color gradient is also used for a gradual blend of color which can be considered as an even wiktionary:gradation, gradation from low to high values, and seen from black to white in the images to the right. Another name for this is ''color progression''. Mathematically, the gradient of a two-variable function (here the image intensity function) at each image point is a 2D vector (geometric), vector with the components given by the derivatives in the horizontal and vertical directions. At each image point, the gradient vector points in the direction of largest possible intensity increase, and the length of the gradient vector corresponds to the rate of change in that direc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Grade (slope)
The grade (US) or gradient (UK) (also called stepth, slope, incline, mainfall, pitch or rise) of a physical feature, landform or constructed line is either the elevation angle of that surface to the horizontal plane, horizontal or its tangent. It is a special case of the slope, where zero indicates horizontal plane, horizontality. A larger number indicates higher or steeper degree of "tilt". Often slope is calculated as a ratio of "rise" to "run", or as a fraction ("rise over run") in which ''run'' is the horizontal distance (not the distance along the slope) and ''rise'' is the vertical distance. Slopes of existing physical features such as canyons and hillsides, bank (geography), stream and river banks, and stream bed, beds are often described as grades, but typically the word "grade" is used for human-made surfaces such as roads, landscape grading, roof pitches, rail tracks, railroads, aqueduct (watercourse), aqueducts, and pedestrian or bicycle routes. The grade may refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Lapse Rate
The lapse rate is the rate at which an atmospheric variable, normally temperature in Earth's atmosphere, falls with altitude. ''Lapse rate'' arises from the word ''lapse'' (in its "becoming less" sense, not its "interruption" sense). In dry air, the adiabatic lapse rate (i.e., decrease in temperature of a parcel of air that rises in the atmosphere without exchanging energy with surrounding air) is 9.8 °C/km (5.4 °F per 1,000 ft). The saturated adiabatic lapse rate (SALR), or moist adiabatic lapse rate (MALR), is the decrease in temperature of a parcel of water-saturated air that rises in the atmosphere. It varies with the temperature and pressure of the parcel and is often in the range 3.6 to (2 to ), as obtained from the International Civil Aviation Organization (ICAO). The environmental lapse rate is the decrease in temperature of air with altitude for a specific time and place (see below). It can be highly variable between circumstances. Lapse rate corresponds to the vertic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Wind Gradient
In common usage, wind gradient, more specifically wind speed gradient or wind velocity gradient, or alternatively shear wind, is the vertical component of the gradient of the mean horizontal wind speed in the lower atmosphere. It is the rate of increase of wind strength with unit increase in height above ground level. In metric units, it is often measured in units of meters per second of speed, per kilometer of height (m/s/km), which reduces inverse milliseconds (ms−1), a unit also used for shear rate. Simple explanation Surface friction forces the surface wind to slow and turn near the surface of the Earth, blowing directly towards the low pressure, when compared to the winds in the nearly frictionless flow well above the Earth's surface. This bottom layer, where surface friction slows the wind and changes the wind direction, is known as the planetary boundary layer. Daytime solar heating due to insolation thickens the boundary layer, as air warmed by contact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sound Speed Gradient
In acoustics, the sound speed gradient is the rate of change of the speed of sound with distance, for example with depth in the ocean, or height in the Earth's atmosphere. A sound speed gradient leads to refraction of sound wavefronts in the direction of lower sound speed, causing the sound rays to follow a curved path. The radius of curvature of the sound path is inversely proportional to the gradient. When the sun warms the Earth's surface, there is a negative temperature gradient in atmosphere. The speed of sound decreases with decreasing temperature, so this also creates a negative sound speed gradient. The sound wave front travels faster near the ground, so the sound is refracted upward, away from listeners on the ground, creating an acoustic shadow at some distance from the source. The opposite effect happens when the ground is covered with snow, or in the morning over water, when the sound speed gradient is positive. In this case, sound waves can be refracted from the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
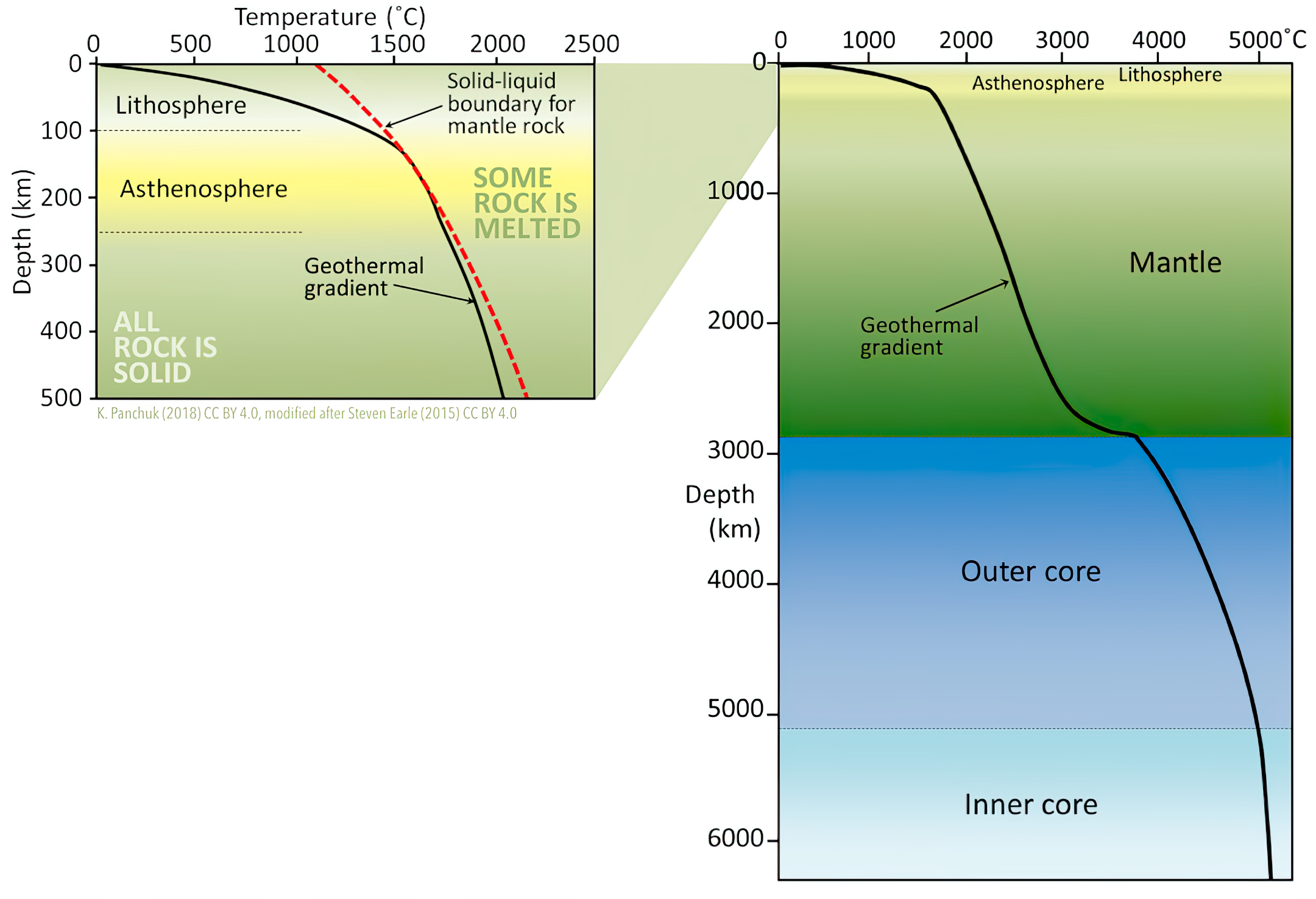 |
Geothermal Gradient
Geothermal gradient is the rate of change in temperature with respect to increasing depth in Earth's interior. As a general rule, the crust temperature rises with depth due to the heat flow from the much hotter mantle; away from tectonic plate boundaries, temperature rises in about 25–30 °C/km (72–87 °F/mi) of depth near the surface in the continental crust. However, in some cases the temperature may drop with increasing depth, especially near the surface, a phenomenon known as or geothermal gradient. The effects of weather, the Sun, and season only reach a depth of roughly . Strictly speaking, ''geo''-thermal necessarily refers to Earth, but the concept may be applied to other planets. In SI units, the geothermal gradient is expressed as °C/km, K/km, or mK/m. These are all equivalent. Earth's internal heat comes from a combination of residual heat from planetary accretion, heat produced through radioactive decay, latent heat from core crystallization, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Temperature Gradient
A temperature gradient is a physical quantity that describes in which direction and at what rate the temperature changes the most rapidly around a particular location. The temperature spatial gradient is a vector quantity with Dimensional analysis, dimension of temperature difference per unit length. The International System of Units, SI Units of measurement, unit is kelvin per meter (K/m). Temperature gradients in the Earth's atmosphere, atmosphere are important in the atmospheric sciences (meteorology, climatology and related fields). Mathematical description Assuming that the temperature ''T'' is an intensive quantity, i.e., a single-valued, Continuous function, continuous and Derivative, differentiable Function (mathematics), function of three-dimensional space (often called a scalar field), i.e., that :T=T(x,y,z) where ''x'', ''y'' and ''z'' are the Cartesian coordinate system, coordinates of the location of interest, then the temperature gradient is the vector (geometric) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |