|
Sextic Curves
In algebra, a sextic (or hexic) polynomial is a polynomial of Degree of a polynomial, degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form: :ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\, where and the ''coefficients'' may be integers, rational numbers, real numbers, complex numbers or, more generally, members of any field (mathematics), field. A sextic function is a function (mathematics), function defined by a sextic polynomial. Because they have an even degree, sextic functions appear similar to quartic functions when graphed, except they may possess an additional Maxima and minima, local maximum and local minimum each. The derivative of a sextic function is a quintic function. Since a sextic function is defined by a polynomial with even degree, it has the same infinite limit when the argument goes to positive or negative infinity. If th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sextic Graph
In algebra, a sextic (or hexic) polynomial is a polynomial of degree six. A sextic equation is a polynomial equation of degree six—that is, an equation whose left hand side is a sextic polynomial and whose right hand side is zero. More precisely, it has the form: :ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\, where and the ''coefficients'' may be integers, rational numbers, real numbers, complex numbers or, more generally, members of any field. A sextic function is a function defined by a sextic polynomial. Because they have an even degree, sextic functions appear similar to quartic functions when graphed, except they may possess an additional local maximum and local minimum each. The derivative of a sextic function is a quintic function. Since a sextic function is defined by a polynomial with even degree, it has the same infinite limit when the argument goes to positive or negative infinity. If the leading coefficient is positive, then the function increases to positive infinity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinity
Infinity is something which is boundless, endless, or larger than any natural number. It is denoted by \infty, called the infinity symbol. From the time of the Ancient Greek mathematics, ancient Greeks, the Infinity (philosophy), philosophical nature of infinity has been the subject of many discussions among philosophers. In the 17th century, with the introduction of the infinity symbol and the infinitesimal calculus, mathematicians began to work with infinite series and what some mathematicians (including Guillaume de l'Hôpital, l'Hôpital and Johann Bernoulli, Bernoulli) regarded as infinitely small quantities, but infinity continued to be associated with endless processes. As mathematicians struggled with the foundation of calculus, it remained unclear whether infinity could be considered as a number or Magnitude (mathematics), magnitude and, if so, how this could be done. At the end of the 19th century, Georg Cantor enlarged the mathematical study of infinity by studying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
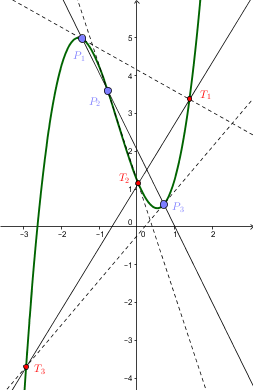
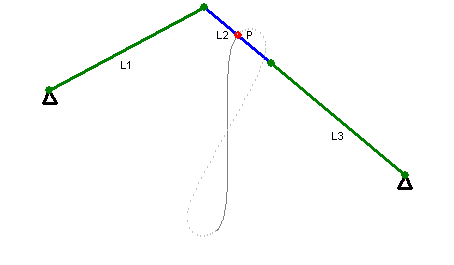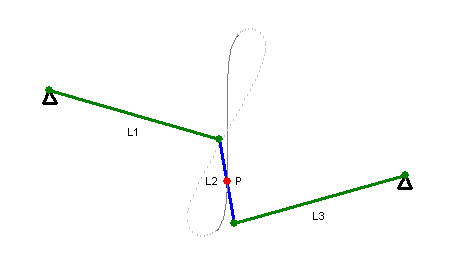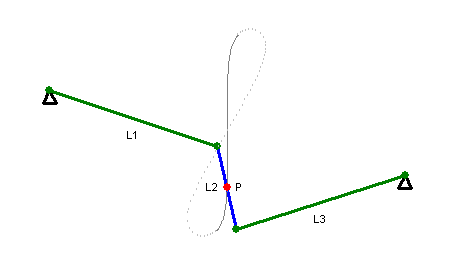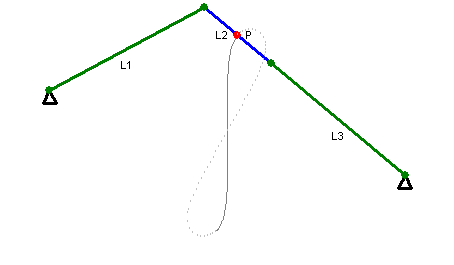
Cayley's Sextic
In geometry, Cayley's sextic (sextic of Cayley, Cayley's sextet) is a plane curve, a member of the sinusoidal spiral family, first discussed by Colin Maclaurin in 1718. Arthur Cayley was the first to study the curve in detail and Raymond Clare Archibald named the curve after him. The curve is symmetric about the ''x''-axis (''y'' = 0) and self-intersects at ''y'' = 0, ''x'' = −''a''/8. Other intercepts are at the origin, at (''a'', 0) and with the ''y''-axis at ±''a'' The curve is the pedal curve (or ''roulette'') of a cardioid with respect to its cusp. Equations of the curve The equation of the curve in polar coordinates is :''r'' = ''4a'' cos3(''θ''/3) In Cartesian coordinates the equation is :4(''x''2 + ''y''2 − (''a''/4)''x'')3 = 27(''a''/4)2(''x''2 + ''y''2)2 . Cayley's sextic may be parametrised (as a periodic function A periodic function, also called a periodic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Suffix
In linguistics, a suffix is an affix which is placed after the stem of a word. Common examples are case endings, which indicate the grammatical case of nouns and adjectives, and verb endings, which form the conjugation of verbs. Suffixes can carry grammatical information (inflectional endings) or lexical information ( derivational/lexical suffixes)''.'' Inflection changes the grammatical properties of a word within its syntactic category. Derivational suffixes fall into two categories: class-changing derivation and class-maintaining derivation. Particularly in the study of Semitic languages, suffixes are called affirmatives, as they can alter the form of the words. In Indo-European studies, a distinction is made between suffixes and endings (see Proto-Indo-European root). A word-final segment that is somewhere between a free morpheme and a bound morpheme is known as a suffixoidKremer, Marion. 1997. ''Person reference and gender in translation: a contrastive investigation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greek Language
Greek (, ; , ) is an Indo-European languages, Indo-European language, constituting an independent Hellenic languages, Hellenic branch within the Indo-European language family. It is native to Greece, Cyprus, Italy (in Calabria and Salento), southern Albania, and other regions of the Balkans, Caucasus, the Black Sea coast, Asia Minor, and the Eastern Mediterranean. It has the list of languages by first written accounts, longest documented history of any Indo-European language, spanning at least 3,400 years of written records. Its writing system is the Greek alphabet, which has been used for approximately 2,800 years; previously, Greek was recorded in writing systems such as Linear B and the Cypriot syllabary. The Greek language holds a very important place in the history of the Western world. Beginning with the epics of Homer, ancient Greek literature includes many works of lasting importance in the European canon. Greek is also the language in which many of the foundational texts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Stem
In linguistics, a word stem is a word part responsible for a word's lexical meaning. The term is used with slightly different meanings depending on the morphology of the language in question. For instance, in Athabaskan linguistics, a verb stem is a root that cannot appear on its own and that carries the tone of the word. Typically, a stem remains unmodified during inflection with few exceptions due to apophony (for example in Polish, ("city") and ("in the city"); in English, ''sing'', ''sang'', and ''sung'', where it can be modified according to morphological rules or peculiarities, such as sandhi). Word stem comparisons across languages have helped reveal cognates that have allowed comparative linguists to determine language families and their history. Root vs stem The word ''friendship'' is made by attaching the morpheme ''-ship'' to the root word ''friend'' (which some linguists also call a stem). While the inflectional plural morpheme ''-s'' can be attached to '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area around Rome, Italy. Through the expansion of the Roman Republic, it became the dominant language in the Italian Peninsula and subsequently throughout the Roman Empire. It has greatly influenced many languages, Latin influence in English, including English, having contributed List of Latin words with English derivatives, many words to the English lexicon, particularly after the Christianity in Anglo-Saxon England, Christianization of the Anglo-Saxons and the Norman Conquest. Latin Root (linguistics), roots appear frequently in the technical vocabulary used by fields such as theology, List of Latin and Greek words commonly used in systematic names, the sciences, List of medical roots, suffixes and prefixes, medicine, and List of Latin legal terms ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. The derivative of a cubic function is a quadratic function. A cubic function with real coefficients has either one or three real roots ( which may not be distinct); all odd-degree polynomials with real coefficients have at least one real root. The graph of a cubic function always has a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steam Engine
A steam engine is a heat engine that performs Work (physics), mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a Cylinder (locomotive), cylinder. This pushing force can be transformed by a connecting rod and Crank (mechanism), crank into rotational force for work. The term "steam engine" is most commonly applied to reciprocating engines as just described, although some authorities have also referred to the steam turbine and devices such as Hero's aeolipile as "steam engines". The essential feature of steam engines is that they are external combustion engines, where the working fluid is separated from the combustion products. The ideal thermodynamic cycle used to analyze this process is called the Rankine cycle. In general usage, the term ''steam engine'' can refer to either complete steam plants (including Boiler (power generation), boilers etc.), such as railway steam locomot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Watt's Curve
In mathematics, Watt's curve is a circular algebraic curve, tricircular algebraic curve, plane algebraic curve of sextic, degree six. It is generated by two circles of radius ''b'' with centers distance 2''a'' apart (taken to be at (±''a'', 0)). A line segment of length 2''c'' attaches to a point on each of the circles, and the midpoint of the line segment traces out the Watt curve as the circles rotate partially back and forth or completely around. It arose in connection with James Watt's pioneering work on the steam engine. The equation of the curve can be given in polar coordinates as :r^2=b^2-\left[a\sin\theta\pm\sqrt\right]^2. Derivation Polar coordinates The polar equation for the curve can be derived as follows: Working in the complex plane, let the centers of the circles be at ''a'' and ''−a'', and the connecting segment have endpoints at ''−a''+''be''''i'' λ and ''a''+''be''''i'' ρ. Let the angle of inclination of the segment be ψ with its midpoint at ''re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stabilizer (group Theory)
In mathematics, a group action of a group G on a set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformations form a group under function composition; for example, the rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that structure. For example, the group of Euclidean isometries acts on Euclidean space and also on the figures drawn i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galois Group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the polynomials that give rise to them via Galois groups is called Galois theory, so named in honor of Évariste Galois who first discovered them. For a more elementary discussion of Galois groups in terms of permutation groups, see the article on Galois theory. Definition Suppose that E is an extension of the field F (written as E/F and read "''E'' over ''F''). An automorphism of E/F is defined to be an automorphism of E that fixes F pointwise. In other words, an automorphism of E/F is an isomorphism \alpha:E\to E such that \alpha(x) = x for each x\in F. The set of all automorphisms of E/F forms a group with the operation of function composition. This group is sometimes denoted by \operatorname(E/F). If E/F is a Galois extension, then \op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |