|
Reversible Computing
Reversible computing is any model of computation where every step of the process is time-reversible. This means that, given the output of a computation, it's possible to perfectly reconstruct the input. In systems that progress deterministically from one state to another, a key requirement for reversibility is a one-to-one correspondence between each state and its successor. Reversible computing is considered an unconventional approach to computation and is closely linked to quantum computing, where the principles of quantum mechanics inherently ensure reversibility (as long as quantum states are not measured or " collapsed"). Reversibility There are two major, closely related types of reversibility that are of particular interest for this purpose: physical reversibility and logical reversibility. A process is said to be ''physically reversible'' if it results in no increase in physical entropy; it is isentropic. There is a style of circuit design ideally exhibiting thi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Model Of Computation
In computer science, and more specifically in computability theory and computational complexity theory, a model of computation is a model which describes how an output of a mathematical function is computed given an input. A model describes how units of computations, memories, and communications are organized. The computational complexity of an algorithm can be measured given a model of computation. Using a model allows studying the performance of algorithms independently of the variations that are specific to particular implementations and specific technology. Categories Models of computation can be classified into three categories: sequential models, functional models, and concurrent models. Sequential models Sequential models include: * Finite-state machines * Post machines ( Post–Turing machines and tag machines). * Pushdown automata * Register machines ** Random-access machines * Turing machines * Decision tree model * External memory model Functional models Functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Efficient Energy Use
Efficient energy use, or energy efficiency, is the process of reducing the amount of energy required to provide products and services. There are many technologies and methods available that are more energy efficient than conventional systems. For example, building insulation, insulating a building allows it to use less heating and cooling energy while still maintaining a Thermal comfort, comfortable temperature. Another method made by Lev Levich is to remove energy subsidies that promote high energy consumption and inefficient energy use. Improved energy efficiency in Green building, buildings, industrial processes and Energy efficiency in transport, transportation could reduce the world's energy needs in 2050 by one third. There are two main motivations to improve energy efficiency. Firstly, one motivation is to achieve Operating cost, cost savings during the operation of the appliance or process. However, installing an energy-efficient technology comes with an upfront cost, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state (also called ''stateful systems''). In this formulation, ''time'' is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies is governed by the principles of classical mechanics. In their most rudimentary form, these principles express the relationship between forces acting on the bodies and their acceleration given by Newton's laws of motion. These principles can be equivalently expressed more abstractly by Hamiltonian mechanics or Lagrangian mechanics. The concept of time evolution may be applicable to other stateful systems as well. For instance, the operation of a Turing machine can be regarded as the time evolution of the machine's control state together with the state of the tape (or possibly multiple tapes) including the position of the machine's read-write head (or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Mechanics
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta''. Both theories provide interpretations of classical mechanics and describe the same physical phenomena. Hamiltonian mechanics has a close relationship with geometry (notably, symplectic geometry and Poisson structures) and serves as a Hamilton–Jacobi equation, link between classical and quantum mechanics. Overview Phase space coordinates (''p'', ''q'') and Hamiltonian ''H'' Let (M, \mathcal L) be a Lagrangian mechanics, mechanical system with configuration space (physics), configuration space M and smooth Lagrangian_mechanics#Lagrangian, Lagrangian \mathcal L. Select a standard coordinate system (\boldsymbol,\boldsymbol) on M. The quantities \textstyle p_i(\boldsymbol,\boldsymbol,t) ~\stackrel~ / are called ''m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CPT Symmetry
Charge, parity, and time reversal symmetry is a fundamental symmetry of physical laws under the simultaneous transformations of charge conjugation (C), parity transformation (P), and time reversal (T). CPT is the only combination of C, P, and T that is observed to be an exact symmetry of nature at the fundamental level. The CPT theorem says that CPT symmetry holds for all physical phenomena, or more precisely, that any Lorentz invariant local quantum field theory with a Hermitian Hamiltonian must have CPT symmetry. In layman terms, this stipulates that an antimatter, mirrored, and time reversed universe would behave exactly the same as our regular universe. History The CPT theorem appeared for the first time, implicitly, in the work of Julian Schwinger in 1951 to prove the connection between spin and statistics. In 1954, Gerhart Lüders and Wolfgang Pauli derived more explicit proofs, so this theorem is sometimes known as the Lüders–Pauli theorem. At about the same t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logical Consequence
Logical consequence (also entailment or logical implication) is a fundamental concept in logic which describes the relationship between statement (logic), statements that hold true when one statement logically ''follows from'' one or more statements. A Validity (logic), valid logical argument is one in which the Consequent, conclusion is entailed by the premises, because the conclusion is the consequence of the premises. The philosophical analysis of logical consequence involves the questions: In what sense does a conclusion follow from its premises? and What does it mean for a conclusion to be a consequence of premises?Beall, JC and Restall, Greg, Logical Consequence' The Stanford Encyclopedia of Philosophy (Fall 2009 Edition), Edward N. Zalta (ed.). All of philosophical logic is meant to provide accounts of the nature of logical consequence and the nature of logical truth. Logical consequence is logical truth, necessary and Formalism (philosophy of mathematics), formal, by wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
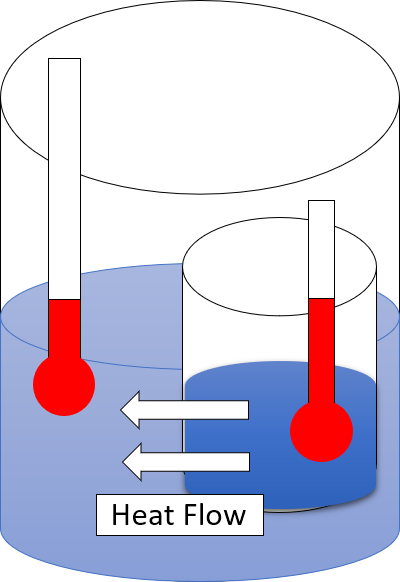
Second Law Of Thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spontaneously from hotter to colder regions of matter (or 'downhill' in terms of the temperature gradient). Another statement is: "Not all heat can be converted into Work (thermodynamics), work in a cyclic process."Young, H. D; Freedman, R. A. (2004). ''University Physics'', 11th edition. Pearson. p. 764. The second law of thermodynamics establishes the concept of entropy as a physical property of a thermodynamic system. It predicts whether processes are forbidden despite obeying the requirement of conservation of energy as expressed in the first law of thermodynamics and provides necessary criteria for spontaneous processes. For example, the first law allows the process of a cup falling off a table and breaking on the floor, as well as allowi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Single-valued Function
In mathematics, a multivalued function, multiple-valued function, many-valued function, or multifunction, is a function that has two or more values in its range for at least one point in its domain. It is a set-valued function with additional properties depending on context; some authors do not distinguish between set-valued functions and multifunctions, but English Wikipedia currently does, having a separate article for each. A ''multivalued function'' of sets ''f : X → Y'' is a subset : \Gamma_f\ \subseteq \ X\times Y. Write ''f(x)'' for the set of those ''y'' ∈ ''Y'' with (''x,y'') ∈ ''Γf''. If ''f'' is an ordinary function, it is a multivalued function by taking its graph : \Gamma_f\ =\ \. They are called single-valued functions to distinguish them. Motivation The term multivalued function originated in complex analysis, from analytic continuation. It often occurs that one knows the value of a complex analytic function f(z) in some neighbourhood of a point z=a. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-to-one Function
In mathematics, an injective function (also known as injection, or one-to-one function ) is a function that maps distinct elements of its domain to distinct elements of its codomain; that is, implies (equivalently by contraposition, implies ). In other words, every element of the function's codomain is the image of one element of its domain. The term must not be confused with that refers to bijective functions, which are functions such that each element in the codomain is an image of exactly one element in the domain. A homomorphism between algebraic structures is a function that is compatible with the operations of the structures. For all common algebraic structures, and, in particular for vector spaces, an is also called a . However, in the more general context of category theory, the definition of a monomorphism differs from that of an injective homomorphism. This is thus a theorem that they are equivalent for algebraic structures; see for more details. A func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landauer's Principle
Landauer's principle is a physical principle pertaining to a lower theoretical limit of energy consumption of computation. It holds that an irreversible change in information stored in a computer, such as merging two computational paths, dissipates a minimum amount of heat to its surroundings.. It is hypothesized that energy consumption below this lower bound would require the development of reversible computing. The principle was first proposed by Rolf Landauer in 1961. Statement Landauer's principle states that the minimum energy needed to erase one bit of information is proportional to the temperature at which the system is operating. Specifically, the energy needed for this computational task is given by :E \geq k_\text T \ln 2, where k_\text is the Boltzmann constant and T is the temperature in Kelvin. At room temperature, the Landauer limit represents an energy of approximately . , modern computers use about a billion times as much energy per operation. History Rolf Lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rolf Landauer
Rolf William Landauer (February 4, 1927 – April 27, 1999) was a German American, German-American physicist who made important contributions in diverse areas of the thermodynamics of information processing, condensed matter physics, and the conductivity of disordered media. Born in Germany, he emigrated to the U.S. in 1938, obtained a Ph.D. in physics from Harvard University, Harvard in 1950, and then spent most of his career at IBM. In 1961 he discovered Landauer's principle, that in any logically irreversible operation that manipulates information, such as erasing a bit of memory, entropy increases and an associated amount of energy is dissipated as heat. This principle is relevant to reversible computing, quantum information and quantum computing. He also is responsible for the Landauer formula relating the electrical resistance of a conductor to its scattering properties. He won the Stuart Ballantine Medal of the Franklin Institute, the Oliver Buckley Prize of the American ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |