|
Quantum Magnetism
A spin model is a mathematical model used in physics primarily to explain magnetism. Spin models may either be classical or quantum mechanical in nature. Spin models have been studied in quantum field theory as examples of integrable models. Spin models are also used in quantum information theory and computability theory in theoretical computer science. The theory of spin models is a far reaching and unifying topic that cuts across many fields. Introduction In ordinary materials, the magnetic dipole moments of individual atoms produce magnetic fields that cancel one another, because each dipole points in a random direction. Ferromagnetic materials below their Curie temperature, however, exhibit magnetic domains in which the atomic dipole moments are locally aligned, producing a macroscopic, non-zero magnetic field from the domain. These are the ordinary "magnets" with which we are all familiar. The study of the behavior of such "spin models" is a thriving area of research in con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kuramoto Model
The Kuramoto model (or Kuramoto–Daido model), first proposed by , is a mathematical model used in describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated by the behavior of systems of chemical and biological process, biological oscillators, and it has found widespread applications in areas such as Neural oscillation#Mathematical description, neuroscience and oscillating flame dynamics. Kuramoto was quite surprised when the behavior of some physical systems, namely coupled arrays of Josephson junctions, followed his model. The model makes several assumptions, including that there is weak coupling, that the oscillators are identical or nearly identical, and that interactions depend sinusoidally on the phase difference between each pair of objects. Definition In the most popular version of the Kuramoto model, each of the oscillators is considered to have its own intrinsic natural frequency ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
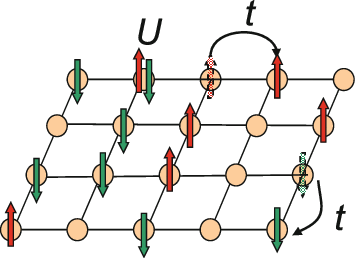
J1 J2 Model
The J1–J2 model is a quantum spin model like the Heisenberg model but also includes a term for the interaction between next-nearest neighbor spins. Hamiltonian In this model, the term J_1 represents the usual nearest-neighbor interaction as seen in the Heisenberg model, and J_2 represents the exchange interaction to the ''next'' nearest-neighbor. : \hat H = J_1 \sum_\vec S_i \cdot \vec S_j + J_2 \sum_ \vec S_i \cdot \vec S_j See also *Spin model *Heisenberg model (quantum) *Hubbard model The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named ... * t-J model * Majumdar–Ghosh model References * * * * *{{cite journal, last1=Majumdar, first1=Chanchal K., last2=Ghosh, first2=Dipan K., title=On Next‐Nearest‐Neighbor Interaction in Linear Chain. II, journal=Journal of Mathematical Phy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hubbard Model
The Hubbard model is an Approximation, approximate model used to describe the transition between Conductor (material), conducting and Electrical insulation, insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard (physicist), John Hubbard. The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian (quantum mechanics), Hamiltonian thus has two terms: a kinetic term allowing for Quantum tunneling, tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heisenberg Model (classical)
In statistical physics, the classical Heisenberg model, developed by Werner Heisenberg, is the n = 3 case of the n-vector model, ''n''-vector model, one of the models used to model ferromagnetism and other phenomena. Definition The classical Heisenberg model can be formulated as follows: take a d-dimensional lattice (group), lattice, and place a set of spins of unit length, :\vec_i \in \mathbb^3, , \vec_i, =1\quad (1), on each lattice node. The model is defined through the following Hamiltonian mechanics, Hamiltonian: : \mathcal = -\sum_ \mathcal_ \vec_i \cdot \vec_j\quad (2) where : \mathcal_ = \begin J & \mboxi, j\mbox \\ 0 & \mbox\end is a coupling between spins. Properties * The general mathematical formalism used to describe and solve the Heisenberg model and certain generalizations is developed in the article on the Potts model. * In the continuum limit the Heisenberg model (2) gives the following equation of motion :: \vec_=\vec\wedge \vec_. :This equation is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bethe Ansatz
In physics, the Bethe ansatz is an ansatz for finding the exact wavefunctions of certain quantum many-body models, most commonly for one-dimensional lattice models. It was first used by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic isotropic (XXX) Heisenberg model. Since then the method has been extended to other spin chains and statistical lattice models. "Bethe ansatz problems" were one of the topics featuring in the "To learn" section of Richard Feynman's blackboard at the time of his death. Discussion In the framework of many-body quantum mechanics, models solvable by the Bethe ansatz can be contrasted with free fermion models. One can say that the dynamics of a free model is one-body reducible: the many-body wave function for fermions (bosons) is the anti-symmetrized (symmetrized) product of one-body wave functions. Models solvable by the Bethe ansatz are not free: the two-body sector has a non-trivial scat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ANNNI Model
In statistical physics, the axial (or anisotropic) next-nearest neighbor Ising model, usually known as the ANNNI model, is a variant of the Ising model. In the ANNNI model, competing ferromagnetic and antiferromagnetic exchange interactions couple spins at nearest and next-nearest neighbor sites along one of the crystallographic axes of the lattice. The model is a prototype for complicated spatially modulated magnetic superstructures in crystals. To describe experimental results on magnetic orderings in erbium, the model was introduced in 1961 by Roger Elliott from the University of Oxford. The model has given its name in 1980 by Michael E. Fisher and Walter Selke, who analysed it first by Monte Carlo methods, and then by low temperature series expansions, showing the fascinating complexity of its phase diagram, including devil's staircases and a Lifshitz point. Indeed, it provides, for two- and three-dimensional systems, a theoretical basis for understanding numerous expe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division (mathematics), division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication (mathematics), multiplication and addition of numbers, are commutative was for many centuries implicitly assumed. Thus, this property was not named until the 19th century, when new algebraic structures started to be studied. Definition A binary operation * on a Set (mathematics), set ''S'' is ''commutative'' if x * y = y * x for all x,y \in S. An operat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, a Hilbert space is a real number, real or complex number, complex inner product space that is also a complete metric space with respect to the metric induced by the inner product. It generalizes the notion of Euclidean space. The inner product allows lengths and angles to be defined. Furthermore, Complete metric space, completeness means that there are enough limit (mathematics), limits in the space to allow the techniques of calculus to be used. A Hilbert space is a special case of a Banach space. Hilbert spaces were studied beginning in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, mathematical formulation of quantum mechanics, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Observables
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum mechanics, an observable is an operator, or gauge, where the property of the quantum state can be determined by some sequence of operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value. Physically meaningful observables must also satisfy transformation laws that relate observations performed by different observers in different frames of reference. These transformation laws are automorphisms of the state space, that is bijective transformations that preserve certain mathematical properties of the space in question. Quantum mechanics In quantum mechanics, observables manifest as self-adjoint operators on a separable complex Hilbert space representing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Chuang
Isaac L. Chuang is an American electrical engineer and physicist. He leads the quanta research group at the Center for Ultracold Atoms at Massachusetts Institute of Technology (MIT). He received his undergraduate degrees in physics (1990) and electrical engineering (1991) and master's in electrical engineering (1991) at MIT.Copsey, D.; Oskin, M.; Impens, F.; Metodiev, T.; Cross, A.; Chong, F.T.; Chuang, I.L.; Kubiatowicz, J., "Toward a scalable, silicon-based quantum computing architecture," IEEE Journal of Selected Topics in Quantum Electronics, vol.9, no.6, pp. 1552–1569, Nov.-Dec. 2003, In 1997 he received his PhD in electrical engineering from Stanford University. Chuang is one of the pioneers of NMR quantum computing. Since 2003, Chuang has focused his attention on trapped ion approaches to quantum computing, as the field of liquid state NMR quantum computing fell out of favor due to limitations on its scalability beyond tens of qubits due to noise. During his time at MI ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |