|
Polyhedral Stellation
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surface. The terms solid polyhedron and polyhedral surface are commonly used to distinguish the two concepts. Also, the term ''polyhedron'' is often used to refer implicitly to the whole structure formed by a solid polyhedron, its polyhedral surface, its faces, its edges, and its vertices. There are many definitions of polyhedron. Nevertheless, the polyhedron is typically understood as a generalization of a two-dimensional polygon and a three-dimensional specialization of a polytope, a more general concept in any number of dimensions. Polyhedra have several general characteristics that include the number of faces, topological classification by Euler characteristic, duality, vertex figures, surface area, volume, interior lines, Dehn invaria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tetrahedron is the simplest of all the ordinary convex polytope, convex polyhedra. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean geometry, Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid (geometry), pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron, the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such net (polyhedron), nets. For any tetrahedron there exists a sphere (called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a " straight line". The noun '' geodesic'' and the adjective '' geodetic'' come from ''geodesy'', the science of measuring the size and shape of Earth, though many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth's surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has since been generalized to more abstract mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph. In a Riemannian manifold or submanifold, geodesics are characterised by the property of havi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
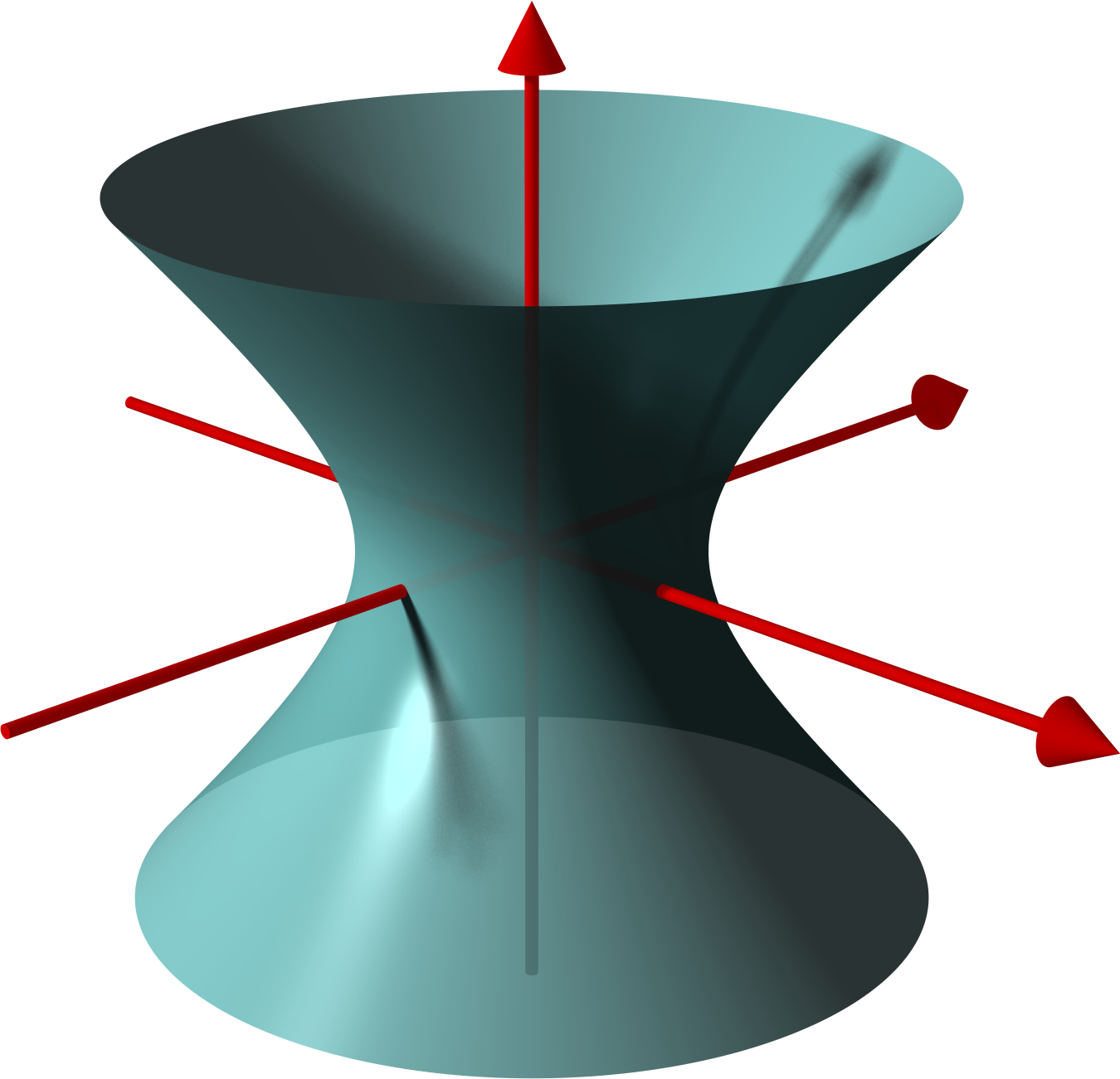
Surface (mathematics)
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line. There are several more precise definitions, depending on the context and the mathematical tools that are used for the study. The simplest mathematical surfaces are planes and spheres in the Euclidean 3-space. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not. A surface is a topological space of dimension two; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a '' coordinate patch'' on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Figure
Solid geometry or stereometry is the geometry of three-dimensional Euclidean space (3D space). A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball consists of a sphere and its interior. Solid geometry deals with the measurements of volumes of various solids, including pyramids, prisms (and other polyhedrons), cubes, cylinders, cones (and truncated cones). History The Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonists. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.Paraphrased and taken in part from the ''1911 Encyclopædia Britannica''. Topics Basic topics in solid geometry and stereometry include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (geometry)
In geometry, a vertex (: vertices or vertexes), also called a corner, is a point (geometry), point where two or more curves, line (geometry), lines, or line segments Tangency, meet or Intersection (geometry), intersect. For example, the point where two lines meet to form an angle and the point where edge (geometry), edges of polygons and polyhedron, polyhedra meet are vertices. Definition Of an angle The ''vertex'' of an angle is the point where two Line (mathematics)#Ray, rays begin or meet, where two line segments join or meet, where two lines intersect (cross), or any appropriate combination of rays, segments, and lines that result in two straight "sides" meeting at one place. :(3 vols.): (vol. 1), (vol. 2), (vol. 3). Of a polytope A vertex is a corner point of a polygon, polyhedron, or other higher-dimensional polytope, formed by the intersection (Euclidean geometry), intersection of Edge (geometry), edges, face (geometry), faces or facets of the object. In a polygon, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge (geometry)
In geometry, an edge is a particular type of line segment joining two vertex (geometry), vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two Face (geometry), faces (or polyhedron sides) meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal. An ''edge'' may also be an infinite line (geometry), line separating two half-planes. The ''sides'' of a plane angle are semi-infinite Half-line (geometry), half-lines (or rays). Relation to edges in graphs In graph theory, an Edge (graph theory), edge is an abstract object connecting two vertex (graph theory), graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment. However, any polyhedron can be represented by its n-s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Face (geometry)
In solid geometry, a face is a flat surface (a Plane (geometry), planar region (mathematics), region) that forms part of the boundary of a solid object. For example, a cube has six faces in this sense. In more modern treatments of the geometry of polyhedra and higher-dimensional polytopes, a "face" is defined in such a way that it may have any dimension. The vertices, edges, and (2-dimensional) faces of a polyhedron are all faces in this more general sense. Polygonal face In elementary geometry, a face is a polygon on the boundary of a polyhedron. (Here a "polygon" should be viewed as including the 2-dimensional region inside it.) Other names for a polygonal face include polyhedron side and Euclidean plane ''tessellation, tile''. For example, any of the six square (geometry), squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polyg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Figure
Solid geometry or stereometry is the geometry of three-dimensional Euclidean space (3D space). A solid figure is the region of 3D space bounded by a two-dimensional closed surface; for example, a solid ball consists of a sphere and its interior. Solid geometry deals with the measurements of volumes of various solids, including pyramids, prisms (and other polyhedrons), cubes, cylinders, cones (and truncated cones). History The Pythagoreans dealt with the regular solids, but the pyramid, prism, cone and cylinder were not studied until the Platonists. Eudoxus established their measurement, proving the pyramid and cone to have one-third the volume of a prism and cylinder on the same base and of the same height. He was probably also the discoverer of a proof that the volume enclosed by a sphere is proportional to the cube of its radius.Paraphrased and taken in part from the ''1911 Encyclopædia Britannica''. Topics Basic topics in solid geometry and stereometry include ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |