|
Mathematical Optimization Software
Given a transformation between input and output values, described by a mathematical function, optimization deals with generating and selecting the best solution from some set of available alternatives, by systematically choosing input values from within an allowed set, computing the output of the function and recording the best output values found during the process. Many real-world problems can be modeled in this way. For example, the inputs could be design parameters for a motor, the output could be the power consumption. For another optimization, the inputs could be business choices and the output could be the profit obtained. An optimization problem, (in this case a minimization problem), can be represented in the following way: :''Given:'' a function ''f'' : ''A'' \to R from some set ''A'' to the real numbers :''Search for:'' an element ''x''0 in ''A'' such that ''f''(''x''0) ≤ ''f''(''x'') for all ''x'' in ''A''. In continuous optimization, ''A'' is some subset of the Eu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Transformation (function)
In mathematics, a transformation, transform, or self-map is a function ''f'', usually with some geometrical underpinning, that maps a set ''X'' to itself, i.e. . Examples include linear transformations of vector spaces and geometric transformations, which include projective transformations, affine transformations, and specific affine transformations, such as rotations, reflections and translations. Partial transformations While it is common to use the term transformation for any function of a set into itself (especially in terms like "transformation semigroup" and similar), there exists an alternative form of terminological convention in which the term "transformation" is reserved only for bijections. When such a narrow notion of transformation is generalized to partial functions, then a partial transformation is a function ''f'': ''A'' → ''B'', where both ''A'' and ''B'' are subsets of some set ''X''. Algebraic structures The set of all transformations on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
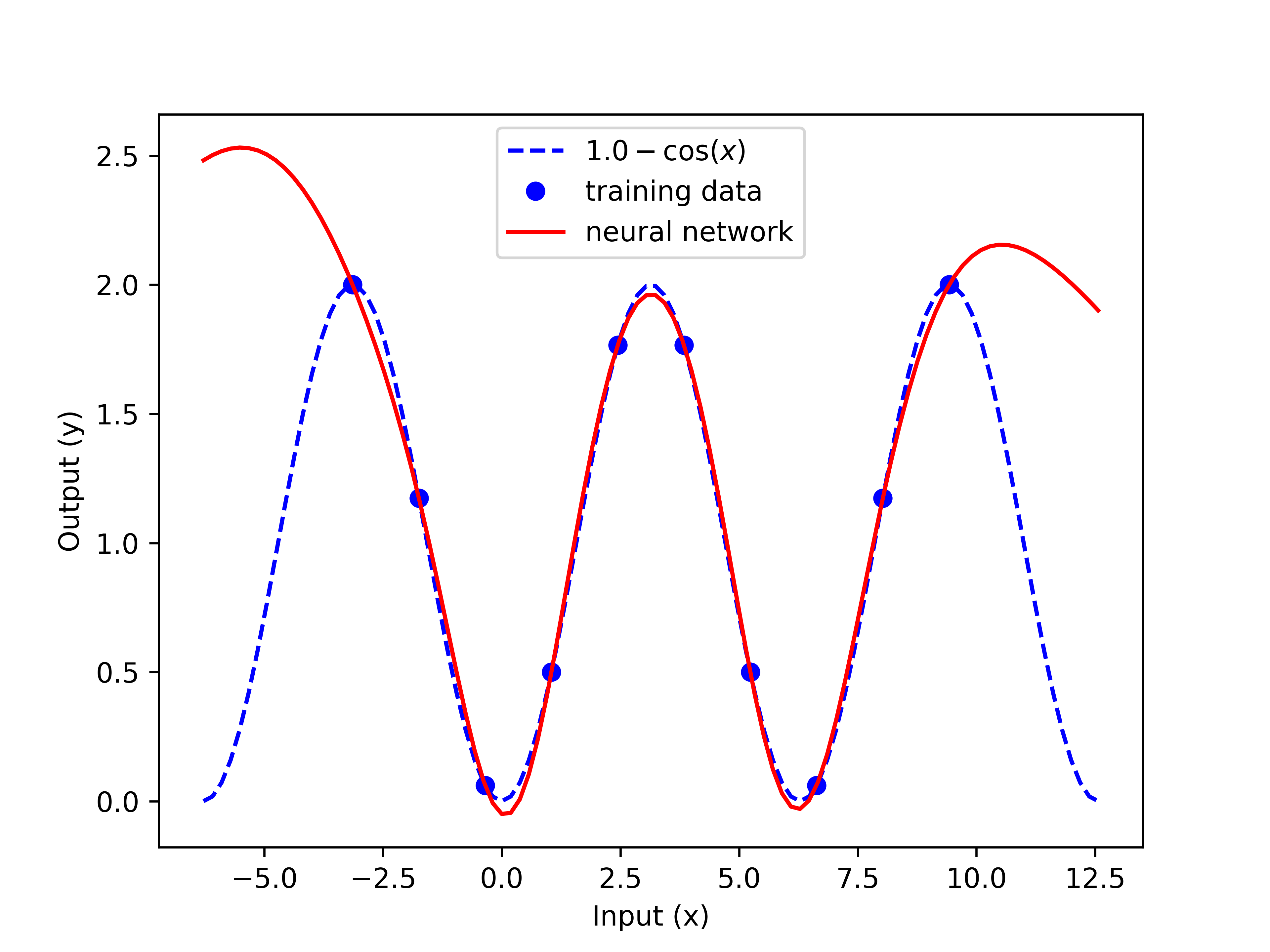 |
Gekko (optimization Software)
The GEKKO Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (IPOPT, APOPT, BPOPT, SNOPT, MINOS_(optimization_software), MINOS). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation. pip install gekko GEKKO works on all platforms and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There are Windows, MacOS, Linux, and ARM (Raspberry Pi) processor options to solve without an Internet connection. GEK ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |