|
Cyclic Sieving
In combinatorial mathematics, cyclic sieving is a phenomenon in which an integer polynomial evaluated at certain roots of unity counts the rotational symmetries of a finite set. Given a family of cyclic sieving phenomena, the polynomials give a ''q''-analogue for the enumeration of the sets, and often arise from an underlying algebraic structure, such as a representation. The first study of cyclic sieving was published by Reiner, Stanton and White in 2004. The phenomenon generalizes the "''q'' = −1 phenomenon" of John Stembridge, which considers evaluations of the polynomial only at the first and second roots of unity (that is, ''q'' = 1 and ''q'' = −1). Definition For every positive integer n, let \omega_n denote the primitive nth root of unity e^. Let X be a finite set with an action of the cyclic group C_n, and let f(q) be an integer polynomial. The triple (X,C_n,f(q)) exhibits the cyclic sieving phenomenon (or CSP) if for every positive integer d dividing n, the num ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
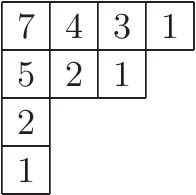
Example Of Cyclic Sieving With Tableaux
Example may refer to: * ''exempli gratia'' (e.g.), usually read out in English as "for example" * .example, reserved as a domain name that may not be installed as a top-level domain of the Internet ** example.com, example.net, example.org, and example.edu: second-level domain names reserved for use in documentation as examples * HMS ''Example'' (P165), an Archer-class patrol and training vessel of the Royal Navy Arts * ''The Example'', a 1634 play by James Shirley * ''The Example'' (comics), a 2009 graphic novel by Tom Taylor and Colin Wilson * Example (musician), the British dance musician Elliot John Gleave (born 1982) * ''Example'' (album), a 1995 album by American rock band For Squirrels See also * Exemplar (other), a prototype or model which others can use to understand a topic better * Exemplum, medieval collections of short stories to be told in sermons * Eixample The Eixample (, ) is a district of Barcelona between the old city (Ciutat Vella) a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called scalar (mathematics), ''scalars''. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. Real vector spaces and complex vector spaces are kinds of vector spaces based on different kinds of scalars: real numbers and complex numbers. Scalars can also be, more generally, elements of any field (mathematics), field. Vector spaces generalize Euclidean vectors, which allow modeling of Physical quantity, physical quantities (such as forces and velocity) that have not only a Magnitude (mathematics), magnitude, but also a Orientation (geometry), direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix (mathematics), matrices, which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Representation Theory Of The Symmetric Group
In mathematics, the representation theory of the symmetric group is a particular case of the representation theory of finite groups, for which a concrete and detailed theory can be obtained. This has a large area of potential applications, from symmetric function theory to quantum chemistry studies of atoms, molecules and solids. The symmetric group S''n'' has order ''n''!. Its conjugacy classes are labeled by partitions of ''n''. Therefore according to the representation theory of a finite group, the number of inequivalent irreducible representations, over the complex numbers, is equal to the number of partitions of ''n''. Unlike the general situation for finite groups, there is in fact a natural way to parametrize irreducible representations by the same set that parametrizes conjugacy classes, namely by partitions of ''n'' or equivalently Young diagrams of size ''n''. Each such irreducible representation can in fact be realized over the integers (every permutation acting by a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hook Length Formula
In combinatorics, combinatorial mathematics, the hook length formula is a formula for the number of Young tableau, standard Young tableaux whose shape is a given Young diagram. It has applications in diverse areas of mathematics, areas such as representation theory, probability theory, probability, and algorithm analysis; for example, the problem of longest increasing subsequences. A related formula gives the number of semi-standard Young tableaux, which is a specialization of a Schur polynomial. Definitions and statement Let \lambda=(\lambda_1\geq \cdots\geq \lambda_k) be a integer partition, partition of n=\lambda_1+\cdots+\lambda_k. It is customary to interpret \lambda graphically as a Young diagram, namely a left-justified array of square cells with k rows of lengths \lambda_1,\ldots,\lambda_k. A (standard) Young tableau of shape \lambda is a filling of the n cells of the Young diagram with all the integers \, with no repetition, such that each row and each column form incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jeu De Taquin
In the mathematical field of combinatorics, jeu de taquin is a construction due to which defines an equivalence relation on the set of skew standard Young tableaux. A jeu de taquin slide is a transformation where the numbers in a tableau are moved around in a way similar to how the pieces in the fifteen puzzle move. Two tableaux are jeu de taquin equivalent if one can be transformed into the other via a sequence of such slides. "Jeu de taquin" (literally "teasing game") is the French name for the fifteen puzzle. Definition of a jeu de taquin slide Given a skew standard Young tableau ''T'' of skew shape \lambda / \mu, pick an adjacent empty cell ''c'' that can be added to the skew diagram \lambda\setminus\mu; what this means is that ''c'' must share at least one edge with some cell in ''T'', and \ \cup \lambda\setminus\mu must also be a skew diagram. There are two kinds of slide, depending on whether ''c'' lies to the upper left of ''T'' or to the lower right. Suppose to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young Tableau
In mathematics, a Young tableau (; plural: tableaux) is a combinatorial object useful in representation theory and Schubert calculus. It provides a convenient way to describe the group representations of the symmetric and general linear groups and to study their properties. Young tableaux were introduced by Alfred Young, a mathematician at Cambridge University, in 1900. They were then applied to the study of the symmetric group by Georg Frobenius in 1903. Their theory was further developed by many mathematicians, including Percy MacMahon, W. V. D. Hodge, G. de B. Robinson, Gian-Carlo Rota, Alain Lascoux, Marcel-Paul Schützenberger and Richard P. Stanley. Definitions ''Note: this article uses the English convention for displaying Young diagrams and tableaux''. Diagrams A Young diagram (also called a Ferrers diagram, particularly when represented using dots) is a finite collection of boxes, or cells, arranged in left-justified rows, with the row lengths in non-incre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Partition
In number theory and combinatorics, a partition of a non-negative integer , also called an integer partition, is a way of writing as a summation, sum of positive integers. Two sums that differ only in the order of their summands are considered the same partition. (If order matters, the sum becomes a composition (combinatorics), composition.) For example, can be partitioned in five distinct ways: : : : : : The only partition of zero is the empty sum, having no parts. The order-dependent composition is the same partition as , and the two distinct compositions and represent the same partition as . An individual summand in a partition is called a part. The number of partitions of is given by the Partition function (number theory), partition function . So . The notation means that is a partition of . Partitions can be graphically visualized with Young diagrams or Ferrers diagrams. They occur in a number of branches of mathematics and physics, including the study of symm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anagram
An anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once. For example, the word ''anagram'' itself can be rearranged into the phrase "nag a ram"; which is an Easter egg suggestion in Google after searching for the word "anagram". The original word or phrase is known as the ''subject'' of the anagram. Any word or phrase that exactly reproduces the letters in another order is an anagram. Someone who creates anagrams may be called an "anagrammatist", and the goal of a serious or skilled anagrammatist is to produce anagrams that reflect or comment on their subject. Examples Anagrams may be created as a commentary on the subject. They may be a parody, a criticism or satire. For example: * "The New York Times, New York Times" = "monkeys write" * "Church of Scientology" = "rich-chosen goofy cult" * "McDonald's restaurants" = "Uncle Sam's standard rot" An anagram may also be a synonym of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorics On Words
Combinatorics on words is a fairly new field of mathematics, branching from combinatorics, which focuses on the study of words and formal languages. The subject looks at letters or symbols, and the sequences they form. Combinatorics on words affects various areas of mathematical study, including algebra and computer science. There have been a wide range of contributions to the field. Some of the first work was on square-free words by Axel Thue in the early 1900s. He and colleagues observed patterns within words and tried to explain them. As time went on, combinatorics on words became useful in the study of algorithms and coding. It led to developments in abstract algebra and answering open questions. Definition Combinatorics is an area of discrete mathematics. Discrete mathematics is the study of countable structures. These objects have a definite beginning and end. The study of enumerable objects is the opposite of disciplines such as analysis, where calculus and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra (or more generally, a module in abstract algebra). In common geometrical contexts, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction. Scalar multiplication is the multiplication of a vector by a scalar (where the product is a vector), and is to be distinguished from inner product of two vectors (where the product is a scalar). Definition In general, if ''K'' is a field and ''V'' is a vector space over ''K'', then scalar multiplication is a function from ''K'' × ''V'' to ''V''. The result of applying this function to ''k'' in ''K'' and v in ''V'' is denoted ''k''v. Properties Scalar multiplication obeys the following rules ''(vector in boldface)'': * Additivity in the scalar: (''c'' + ''d'')v = ''c''v + ''d''v; * Additivity in the vector: ''c''(v + w) = ''c''v + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Character (mathematics)
In mathematics, a character is (most commonly) a special kind of function from a group to a field (such as the complex numbers). There are at least two distinct, but overlapping meanings. Other uses of the word "character" are almost always qualified. Multiplicative character A multiplicative character (or linear character, or simply character) on a group ''G'' is a group homomorphism from ''G'' to the multiplicative group of a field , usually the field of complex numbers. If ''G'' is any group, then the set Ch(''G'') of these morphisms forms an abelian group under pointwise multiplication. This group is referred to as the character group of ''G''. Sometimes only ''unitary'' characters are considered (thus the image is in the unit circle); other such homomorphisms are then called ''quasi-characters''. Dirichlet characters can be seen as a special case of this definition. Multiplicative characters are linearly independent, i.e. if \chi_1,\chi_2, \ldots , \chi_n are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trace (linear Algebra)
In linear algebra, the trace of a square matrix , denoted , is the sum of the elements on its main diagonal, a_ + a_ + \dots + a_. It is only defined for a square matrix (). The trace of a matrix is the sum of its eigenvalues (counted with multiplicities). Also, for any matrices and of the same size. Thus, similar matrices have the same trace. As a consequence, one can define the trace of a linear operator mapping a finite-dimensional vector space into itself, since all matrices describing such an operator with respect to a basis are similar. The trace is related to the derivative of the determinant (see Jacobi's formula). Definition The trace of an square matrix is defined as \operatorname(\mathbf) = \sum_^n a_ = a_ + a_ + \dots + a_ where denotes the entry on the row and column of . The entries of can be real numbers, complex numbers, or more generally elements of a field . The trace is not defined for non-square matrices. Example Let be a matrix, with \m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |