|
Critical Point (network Science)
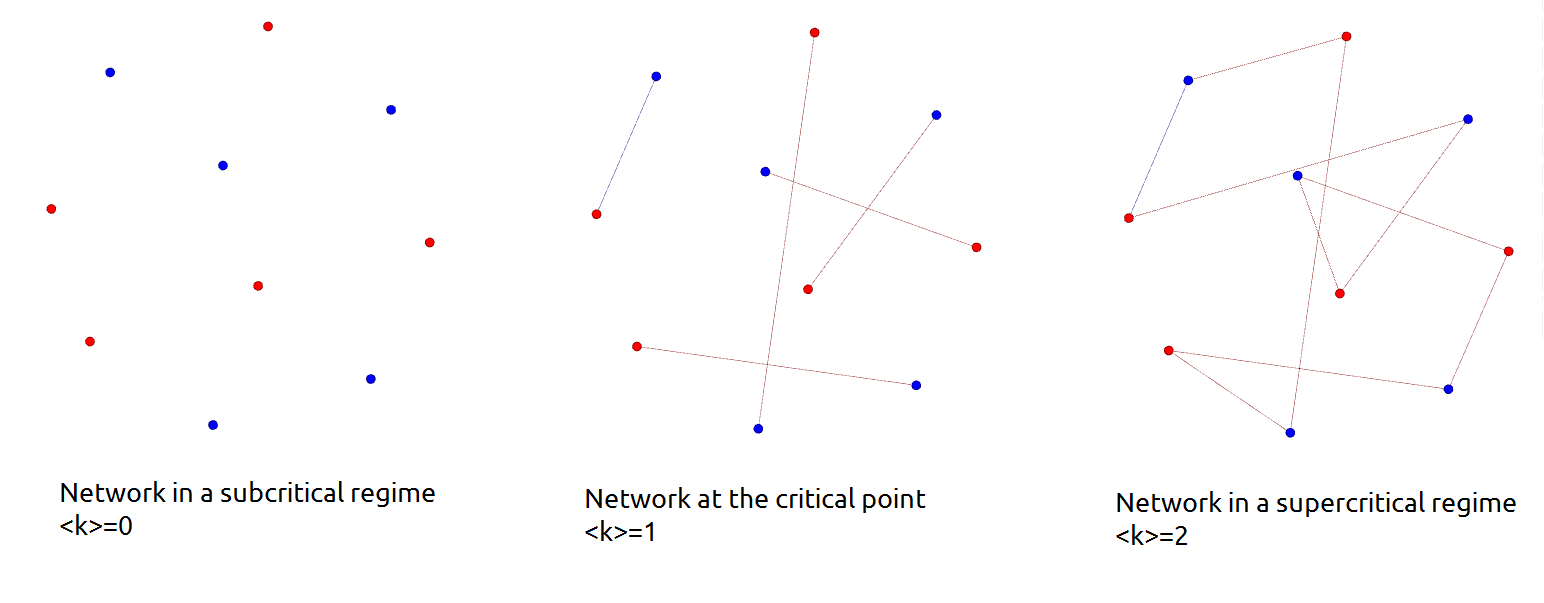
In network science, a critical point is a value of average degree, which separates random networks that have a giant component from those that do not (i.e. it separates a network in a subcritical regime from one in a supercritical regime). Considering a random network with an average degree \langle k\rangle the critical point is \langle k\rangle = 1 where the average degree is defined by the fraction of the number of edges (e) and nodes (N) in the network, that is \langle k\rangle =\frac. Subcritical regime In a subcritical regime the network has no giant component, only small clusters. In the special case of \langle k\rangle =0 the network is not connected at all. A random network is in a subcritical regime until the average degree exceeds the critical point, that is the network is in a subcritical regime as long as \langle k\rangle 1. Example on different regimes Consider a speed dating event as an example, with the participants as the nodes of the network. At the begi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, Cognitive network, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential statistics, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Average Degree
In ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean the sum of the numbers divided by how many numbers are in the list. For example, the mean or average of the numbers 2, 3, 4, 7, and 9 (summing to 25) is 5. Depending on the context, the most representative statistic to be taken as the average might be another measure of central tendency, such as the mid-range, median, mode or geometric mean. For example, the average personal income is often given as the median the number below which are 50% of personal incomes and above which are 50% of personal incomes because the mean would be higher by including personal incomes from a few billionaires. General properties If all numbers in a list are the same number, then their average is also equal to this number. This property is shared by each of the many types of average. Another universal pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Giant Component
In network theory, a giant component is a connected component of a given random graph that contains a significant fraction of the entire graph's vertices. More precisely, in graphs drawn randomly from a probability distribution over arbitrarily large graphs, a giant component is a connected component whose fraction of the overall number of vertices is bounded away from zero. In sufficiently dense graphs distributed according to the Erdős–Rényi model, a giant component exists with high probability. Giant component in Erdős–Rényi model Giant components are a prominent feature of the Erdős–Rényi model (ER) of random graphs, in which each possible edge connecting pairs of a given set of vertices is present, independently of the other edges, with probability . In this model, if p \le \frac for any constant \epsilon>0, then with high probability (in the limit as n goes to infinity) all connected components of the graph have size , and there is no giant component. However, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction). Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete graphs, with their vertices placed on the points of a regular polygon, had already appeared in the 13th century, in the work of Ramon Llull. Such a drawing is sometimes referred to as a mystic rose. Properties The complete graph on vertices is denoted by . Some sources claim that the letter in this notation stands for the German word , but the German name for a complete graph, , does not contain the letter , and other sources state that the notation honors the contributions of Kazimierz Kuratowski to graph theory. has edg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network In Different Regimes
Network, networking and networked may refer to: Science and technology * Network theory, the study of graphs as a representation of relations between discrete objects * Network science, an academic field that studies complex networks Mathematics * Networks, a graph with attributes studied in network theory ** Scale-free network, a network whose degree distribution follows a power law ** Small-world network, a mathematical graph in which most nodes are not neighbors, but have neighbors in common * Flow network, a directed graph where each edge has a capacity and each edge receives a flow Biology * Biological network, any network that applies to biological systems * Ecological network, a representation of interacting species in an ecosystem * Neural network, a network or circuit of neurons Technology and communication * Artificial neural network, a computing system inspired by animal brains * Broadcast network, radio stations, television stations, or other electronic media outlets ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Speed Dating
Speed dating is a formalized matchmaking process with the purpose of encouraging eligible singles to meet new potential partners in a very short period of time, so that interested pairs can continue meeting each other after the event. Organization Usually, advance registration is required for speed dating events. Participants are rotated to meet each other over a series of short "Dating, dates" typically lasting from three to eight minutes depending on the organization running the event. At the end of each interval a signal (e.g., a ringing bell, glass clinks or a whistle blow) is given to alert participants to move on to the next date. When the event concludes, participants can submit a list to the organizers of candidates they would like to share their contact information with. The organizers will forward the contact information if both participants included each other on the list. Contact information cannot be exchanged during the initial meeting to reduce pressure when acc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percolation Theory
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger Glossary of graph theory, connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles Network theory and Percolation (cognitive psychology). Introduction A representative question (and the etymology, source of the name) is as follows. Assume that some liquid is poured on top of some porosity, porous material. Will the liquid be able to make its way from hole to hole and reach the bottom? This physical question is mathematical model, modelled mathematically as a Grid graph, three-dimensional network of graph (discrete mathematics), vertices, usually called "sites", in which the graph (dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Graph
In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of ''typical'' graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, ''random graph'' refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a ''random graph''. Models A random graph is obtained by starting with a set of ''n'' isolated vertices and adding successive edges between them at random. The a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Networks
Network, networking and networked may refer to: Science and technology * Network theory, the study of graphs as a representation of relations between discrete objects * Network science, an academic field that studies complex networks Mathematics * Networks, a graph with attributes studied in network theory ** Scale-free network, a network whose degree distribution follows a power law ** Small-world network, a mathematical graph in which most nodes are not neighbors, but have neighbors in common * Flow network, a directed graph where each edge has a capacity and each edge receives a flow Biology * Biological network, any network that applies to biological systems * Ecological network, a representation of interacting species in an ecosystem * Neural network, a network or circuit of neurons Technology and communication * Artificial neural network, a computing system inspired by animal brains * Broadcast network, radio stations, television stations, or other electronic media ou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |