|
Consistent Estimator
In statistics, a consistent estimator or asymptotically consistent estimator is an estimator—a rule for computing estimates of a parameter ''θ''0—having the property that as the number of data points used increases indefinitely, the resulting sequence of estimates converges in probability to ''θ''0. This means that the distributions of the estimates become more and more concentrated near the true value of the parameter being estimated, so that the probability of the estimator being arbitrarily close to ''θ''0 converges to one. In practice one constructs an estimator as a function of an available sample of size ''n'', and then imagines being able to keep collecting data and expanding the sample ''ad infinitum''. In this way one would obtain a sequence of estimates indexed by ''n'', and consistency is a property of what occurs as the sample size “grows to infinity”. If the sequence of estimates can be mathematically shown to converge in probability to the true value '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Consistency Of Estimator
In deductive logic, a consistent theory is one that does not lead to a logical contradiction. A theory T is consistent if there is no formula \varphi such that both \varphi and its negation \lnot\varphi are elements of the set of consequences of T. Let A be a set of closed sentences (informally "axioms") and \langle A\rangle the set of closed sentences provable from A under some (specified, possibly implicitly) formal deductive system. The set of axioms A is consistent when there is no formula \varphi such that \varphi \in \langle A \rangle and \lnot \varphi \in \langle A \rangle. A ''trivial'' theory (i.e., one which proves every sentence in the language of the theory) is clearly inconsistent. Conversely, in an explosive formal system (e.g., classical or intuitionistic propositional or first-order logics) every inconsistent theory is trivial. Consistency of a theory is a syntactic notion, whose semantic counterpart is satisfiability. A theory is satisfiable if it has a model, i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Continuous Mapping Theorem
In probability theory, the continuous mapping theorem states that continuous functions preserve limits even if their arguments are sequences of random variables. A continuous function, in Heine's definition, is such a function that maps convergent sequences into convergent sequences: if ''xn'' → ''x'' then ''g''(''xn'') → ''g''(''x''). The ''continuous mapping theorem'' states that this will also be true if we replace the deterministic sequence with a sequence of random variables , and replace the standard notion of convergence of real numbers “→” with one of the types of convergence of random variables. This theorem was first proved by Henry Mann and Abraham Wald in 1943, and it is therefore sometimes called the Mann–Wald theorem. Meanwhile, Denis Sargan refers to it as the general transformation theorem. Statement Let , ''X'' be random elements defined on a metric space ''S''. Suppose a function (where ''S′'' is another metric space) has the set of discontin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
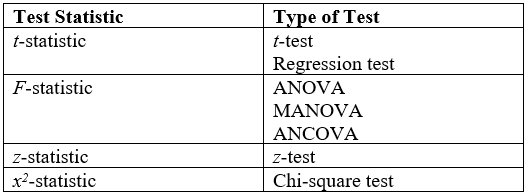 |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a Critical value (statistics), critical value or equivalently by evaluating a p-value, ''p''-value computed from the test statistic. Roughly 100 list of statistical tests, specialized statistical tests are in use and noteworthy. History While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Choice of null hypothesis Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Regression Dilution
Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero (the underestimation of its absolute value), caused by errors in the independent variable. Consider fitting a straight line for the relationship of an outcome variable ''y'' to a predictor variable ''x'', and estimating the slope of the line. Statistical variability, measurement error or random noise in the ''y'' variable causes uncertainty in the estimated slope, but not bias: on average, the procedure calculates the right slope. However, variability, measurement error or random noise in the ''x'' variable causes bias in the estimated slope (as well as imprecision). The greater the variance in the ''x'' measurement, the closer the estimated slope must approach zero instead of the true value. It may seem counter-intuitive that noise in the predictor variable ''x'' induces a bias, but noise in the outcome variable ''y'' does not. Recall that linear regressi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Fisher Consistency
In statistics, Fisher consistency, named after Ronald Fisher, is a desirable property of an estimator asserting that if the estimator were calculated using the entire population rather than a sample, the true value of the estimated parameter would be obtained. Definition Suppose we have a statistical sample ''X''1, ..., ''X''''n'' where each ''X''''i'' follows a cumulative distribution ''F''''θ'' which depends on an unknown parameter ''θ''. If an estimator of ''θ'' based on the sample can be represented as a functional of the empirical distribution function ''F̂n'': :\hat =T(\hat F_n) \,, the estimator is said to be ''Fisher consistent'' if: :T(F_\theta) = \theta \, . As long as the ''X''''i'' are exchangeable, an estimator ''T'' defined in terms of the ''X''''i'' can be converted into an estimator ''T′'' that can be defined in terms of ''F̂n'' by averaging ''T'' over all permutations of the data. The resulting estimator will have the same expected value as ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Efficient Estimator
In statistics, efficiency is a measure of quality of an estimator, of an experimental design, or of a hypothesis testing procedure. Essentially, a more efficient estimator needs fewer input data or observations than a less efficient one to achieve the Cramér–Rao bound. An ''efficient estimator'' is characterized by having the smallest possible variance, indicating that there is a small deviance between the estimated value and the "true" value in the L2 norm sense. The relative efficiency of two procedures is the ratio of their efficiencies, although often this concept is used where the comparison is made between a given procedure and a notional "best possible" procedure. The efficiencies and the relative efficiency of two procedures theoretically depend on the sample size available for the given procedure, but it is often possible to use the asymptotic relative efficiency (defined as the limit of the relative efficiencies as the sample size grows) as the principal comparison ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Degrees Of Freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary. Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the estimate of a parameter is called the degrees of freedom. In general, the degrees of freedom of an estimate of a parameter are equal to the number of independent scores that go into the estimate minus the number of parameters used as intermediate steps in the estimation of the parameter itself. For example, if the variance is to be estimated from a random sample of N independent scores, then the degrees of freedom is equal to the number of independent scores (''N'') minus the number of parameters estimated as intermediate steps (one, namely, the sample mean) and is therefore equal to N-1. Mathematically, degrees of freedom is the number of dimensions of the domain of a random vector, or e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Bessel's Correction
In statistics, Bessel's correction is the use of ''n'' − 1 instead of ''n'' in the formula for the sample variance and sample standard deviation, where ''n'' is the number of observations in a sample. This method corrects the bias in the estimation of the population variance. It also partially corrects the bias in the estimation of the population standard deviation. However, the correction often increases the mean squared error in these estimations. This technique is named after Friedrich Bessel. Formulation In estimating the population variance from a sample when the population mean is unknown, the uncorrected sample variance is the ''mean'' of the squares of deviations of sample values from the sample mean (i.e., using a multiplicative factor 1/''n''). In this case, the sample variance is a biased estimator of the population variance. Multiplying the uncorrected sample variance by the factor : \frac n gives an ''unbiased'' estimator of the population varia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sample Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its mean. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek letter σ (sigma), for the population standard deviation, or the Latin letter '' s'', for the sample standard deviation. The standard deviation of a random variable, sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, variance is the average of the squared deviations from the mean.) A useful property of the sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Sample Variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers is spread out from their average value. It is the second central moment of a distribution, and the covariance of the random variable with itself, and it is often represented by \sigma^2, s^2, \operatorname(X), V(X), or \mathbb(X). An advantage of variance as a measure of dispersion is that it is more amenable to algebraic manipulation than other measures of dispersion such as the expected absolute deviation; for example, the variance of a sum of uncorrelated random variables is equal to the sum of their variances. A disadvantage of the variance for practical applications is that, unlike the standard deviation, its units differ from the random variable, which is why the standard devia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Biased Estimator
In statistics, the bias of an estimator (or bias function) is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called ''unbiased''. In statistics, "bias" is an property of an estimator. Bias is a distinct concept from consistency: consistent estimators converge in probability to the true value of the parameter, but may be biased or unbiased (see bias versus consistency for more). All else being equal, an unbiased estimator is preferable to a biased estimator, although in practice, biased estimators (with generally small bias) are frequently used. When a biased estimator is used, bounds of the bias are calculated. A biased estimator may be used for various reasons: because an unbiased estimator does not exist without further assumptions about a population; because an estimator is difficult to compute (as in unbiased estimation of standard deviation); because a biased estima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Stochastic Equicontinuity
In estimation theory in statistics, stochastic equicontinuity is a property of estimators (estimation procedures) that is useful in dealing with their asymptotic behaviour as the amount of data increases. It is a version of equicontinuity used in the context of functions of random variables: that is, random functions. The property relates to the rate of convergence of sequences of random variables and requires that this rate is essentially the same within a region of the parameter space being considered. For instance, stochastic equicontinuity, along with other conditions, can be used to show uniform weak convergence, which can be used to prove the convergence of extremum estimators. Definition Let \ be a family of random functions defined from \Theta \rightarrow \reals, where \Theta is any normed metric space. Here \ might represent a sequence of estimators applied to datasets of size ''n'', given that the data arises from a population for which the parameter indexing the st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |