|
Configuration Space (physics)
In classical mechanics, the parameters that define the configuration of a system are called '' generalized coordinates,'' and the space defined by these coordinates is called the configuration space of the physical system. It is often the case that these parameters satisfy mathematical constraints, such that the set of actual configurations of the system is a manifold in the space of generalized coordinates. This manifold is called the configuration manifold of the system. Notice that this is a notion of "unrestricted" configuration space, i.e. in which different point particles may occupy the same position. In mathematics, in particular in topology, a notion of "restricted" configuration space is mostly used, in which the diagonals, representing "colliding" particles, are removed. Examples A particle in 3D space The position of a single particle moving in ordinary Euclidean 3-space is defined by the vector q=(x,y,z), and therefore its ''configuration space'' is Q=\mathbb^3. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Classical Mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics involved Scientific Revolution, substantial change in the methods and philosophy of physics. The qualifier ''classical'' distinguishes this type of mechanics from physics developed after the History of physics#20th century: birth of modern physics, revolutions in physics of the early 20th century, all of which revealed limitations in classical mechanics. The earliest formulation of classical mechanics is often referred to as Newtonian mechanics. It consists of the physical concepts based on the 17th century foundational works of Sir Isaac Newton, and the mathematical methods invented by Newton, Gottfried Wilhelm Leibniz, Leonhard Euler and others to describe the motion of Physical body, bodies under the influence of forces. Later, methods bas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Inverse Kinematics
In computer animation and robotics, inverse kinematics is the mathematical process of calculating the variable joint parameters needed to place the end of a kinematic chain, such as a robot manipulator or animation character's skeleton, in a given position and orientation relative to the start of the chain. Given joint parameters, the position and orientation of the chain's end, e.g. the hand of the character or robot, can typically be calculated directly using multiple applications of trigonometric formulas, a process known as forward kinematics. However, the reverse operation is, in general, much more challenging. Inverse kinematics is also used to recover the movements of an object in the world from some other data, such as a film of those movements, or a film of the world as seen by a camera which is itself making those movements. This occurs, for example, where a human actor's filmed movements are to be duplicated by an animated character. Robotics In robotics, inverse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
UC Berkeley
The University of California, Berkeley (UC Berkeley, Berkeley, Cal, or California), is a public land-grant research university in Berkeley, California, United States. Founded in 1868 and named after the Anglo-Irish philosopher George Berkeley, it is the state's first land-grant university and is the founding campus of the University of California system. Berkeley has an enrollment of more than 45,000 students. The university is organized around fifteen schools of study on the same campus, including the College of Chemistry, the College of Engineering, College of Letters and Science, and the Haas School of Business. It is classified among "R1: Doctoral Universities – Very high research activity". Lawrence Berkeley National Laboratory was originally founded as part of the university. Berkeley was a founding member of the Association of American Universities and was one of the original eight " Public Ivy" schools. In 2021, the federal funding for campus research and dev ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Parameter Space
The parameter space is the space of all possible parameter values that define a particular mathematical model. It is also sometimes called weight space, and is often a subset of finite-dimensional Euclidean space. In statistics, parameter spaces are particularly useful for describing parametric families of probability distributions. They also form the background for parameter estimation. In the case of extremum estimators for parametric models, a certain objective function is maximized or minimized over the parameter space. Theorems of existence and consistency of such estimators require some assumptions about the topology of the parameter space. For instance, compactness of the parameter space, together with continuity of the objective function, suffices for the existence of an extremum estimator. Sometimes, parameters are analyzed to view how they affect their statistical model. In that context, they can be viewed as inputs of a function, in which case the technical term for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Feature Space
Feature may refer to: Computing * Feature recognition, could be a hole, pocket, or notch * Feature (computer vision), could be an edge, corner or blob * Feature (machine learning), in statistics: individual measurable properties of the phenomena being observed * Software feature, a distinguishing characteristic of a software program Science and analysis * Feature data, in geographic information systems, comprise information about an entity with a geographic location * Features, in audio signal processing, an aim to capture specific aspects of audio signals in a numeric way * Feature (archaeology), any dug, built, or dumped evidence of human activity Media * Feature film, a film with a running time long enough to be considered the principal or sole film to fill a program ** Feature length, the standardized length of such films * Feature story, a piece of non-fiction writing about news * Radio documentary (feature), a radio program devoted to covering a particular topic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Wave Function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter), psi, respectively). Wave functions are complex number, complex-valued. For example, a wave function might assign a complex number to each point in a region of space. The Born rule provides the means to turn these complex probability amplitudes into actual probabilities. In one common form, it says that the squared modulus of a wave function that depends upon position is the probability density function, probability density of measurement in quantum mechanics, measuring a particle as being at a given place. The integral of a wavefunction's squared modulus over all the system's degrees of freedom must be equal to 1, a condition called ''normalization''. Since the wave function is complex-valued, only its relative phase and relative magnitud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Bloch Sphere
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system ( qubit), named after the physicist Felix Bloch. Mathematically each quantum mechanical system is associated with a separable complex Hilbert space H. A pure state of a quantum system is represented by a non-zero vector \psi in H. As the vectors \psi and \lambda \psi (with \lambda \in \mathbb^*) represent the same state, the level of the quantum system corresponds to the dimension of the Hilbert space and pure states can be represented as equivalence classes, or, rays in a projective Hilbert space \mathbf(H_)=\mathbb\mathbf^. For a two-dimensional Hilbert space, the space of all such states is the complex projective line \mathbb\mathbf^1. This is the Bloch sphere, which can be mapped to the Riemann sphere. The Bloch sphere is a unit 2-sphere, with antipodal points corresponding to a pair of mutually orthogonal state vec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Complex Projective Line
In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane (also called the closed complex plane): the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value \infty for infinity. With the Riemann model, the point \infty is near to very large numbers, just as the point 0 is near to very small numbers. The extended complex numbers are useful in complex analysis because they allow for division by zero in some circumstances, in a way that makes expressions such as 1/0=\infty well-behaved. For example, any rational function on the complex plane can be extended to a holomorphic function on the Riemann sphere, with the poles of the rational function mapping to infinity. More generally, any meromorphic function can be thought of as a holomorphic function whose codomain is the Riemann sphere. In geometry, the Riemann sphere is the prototypical ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Quantum State Space
In physics, a quantum state space is an abstract space in which different "positions" represent not literal locations, but rather quantum states of some physical system. It is the quantum analog of the phase space of classical mechanics. Relative to Hilbert space In quantum mechanics a state space is a Hilbert_space#Separable_spaces, separable complex number, complex Hilbert space. The dimension (vector space), dimension of this Hilbert space depends on the system we choose to describe. The different states that could come out of any particular measurement form an orthonormal basis, so any quantum state, state vector in the state space can be written as a linear combination of these basis vectors. Having a nonzero component along multiple dimensions is called a Quantum superposition, superposition. In the Mathematical formulation of quantum mechanics, formalism of quantum mechanics these quantum state, state vectors are often written using Paul Dirac, Dirac's compact bra–ket ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Mott Problem
The Mott problem is an iconic challenge to quantum mechanics theory: how can the prediction of spherically symmetric wave function result in linear tracks seen in a cloud chamber. The problem was first formulated in 1927 by Albert Einstein and Max Born and solved in 1929 by Nevill Francis Mott. Mott's solution notably only uses the wave equation, not wavefunction collapse, and it is considered the earliest example of what is now called decoherence theory. Spherical waves, particle tracks The problem later associated with Mott concerns a spherical wave function associated with an alpha ray emitted from the decay of a radioactive atomic nucleus. Intuitively, one might think that such a wave function should randomly ionize atoms throughout the cloud chamber, but this is not the case. The result of such a decay is always observed as linear tracks seen in Wilson's cloud chamber. The origin of the tracks given the original spherical wave predicted by theory is the problem requiring p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
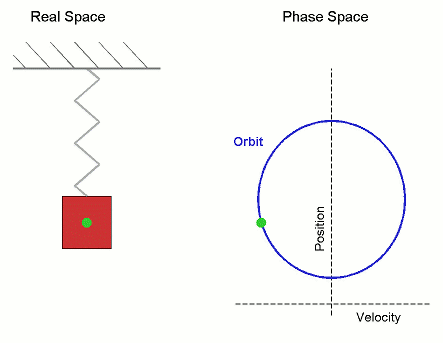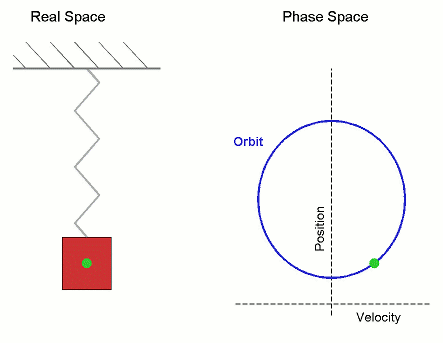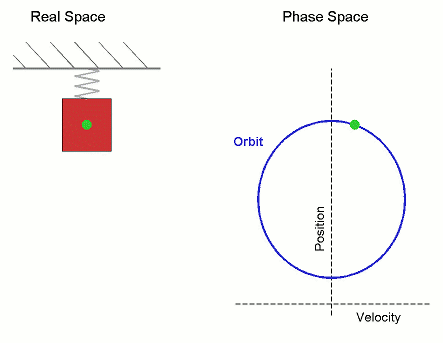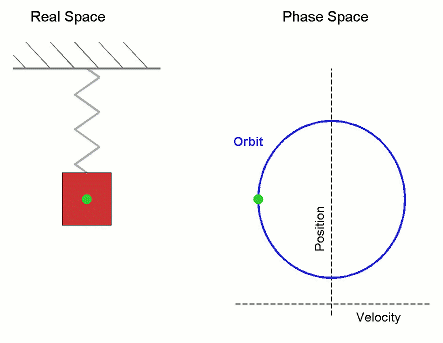 |
Phase Space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space. The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs. Principles In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |