|
Compressed Sensing
Compressed sensing (also known as compressive sensing, compressive sampling, or sparse sampling) is a signal processing technique for efficiently acquiring and reconstructing a Signal (electronics), signal by finding solutions to Underdetermined system, underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals. Compressed sensing has applications in, for example, magnetic resonance imaging (MRI) where the incoherence condition is typically satisfied. Overview A common goal of the engineering field of signal processing is to reconstruct a signal from a series ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polytope. A linear programming algorithm finds a point in the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Underdetermined System
In mathematics, a system of linear equations or a system of polynomial equations is considered underdetermined if there are fewer equations than unknowns (in contrast to an overdetermined system, where there are more equations than unknowns). The terminology can be explained using the concept of constraint counting. Each unknown can be seen as an available degree of freedom. Each equation introduced into the system can be viewed as a constraint that restricts one degree of freedom. Therefore, the critical case (between overdetermined and underdetermined) occurs when the number of equations and the number of free variables are equal. For every variable giving a degree of freedom, there exists a corresponding constraint removing a degree of freedom. An indeterminate system additional constraints that are not equations, such as restricting the solutions to integers. The underdetermined case, by contrast, occurs when the system has been underconstrained—that is, when the unknown ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sparse Matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse but a common criterion is that the number of non-zero elements is roughly equal to the number of rows or columns. By contrast, if most of the elements are non-zero, the matrix is considered dense. The number of zero-valued elements divided by the total number of elements (e.g., ''m'' × ''n'' for an ''m'' × ''n'' matrix) is sometimes referred to as the sparsity of the matrix. Conceptually, sparsity corresponds to systems with few pairwise interactions. For example, consider a line of balls connected by springs from one to the next: this is a sparse system, as only adjacent balls are coupled. By contrast, if the same line of balls were to have springs connecting each ball to all other balls, the system would correspond to a dense matrix. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basis Pursuit
Basis pursuit is the mathematical optimization problem of the form : \min_x \, x\, _1 \quad \text \quad y = Ax, where ''x'' is a ''N''-dimensional solution vector (signal), ''y'' is a ''M''-dimensional vector of observations (measurements), ''A'' is a ''M'' × ''N'' transform matrix (usually measurement matrix) and ''M'' < ''N''. The version of basis pursuit that seeks to minimize the ''L''0 norm is NP-hard. It is usually applied in cases where there is an of linear equations ''y'' = ''Ax'' that must be exactly satisfied, and the sparsest solution in the ''L''1 sense is desired. When it is desirable to trade off exact equality of ''Ax'' and ''y'' in exchange for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The Royal Statistical Society, Series B
A journal, from the Old French ''journal'' (meaning "daily"), may refer to: *Bullet journal, a method of personal organization *Diary, a record of personal secretive thoughts and as open book to personal therapy or used to feel connected to oneself. A record of what happened over the course of a day or other period *Daybook, also known as a general journal, a daily record of financial transactions *Logbook, a record of events important to the operation of a vehicle, facility, or otherwise *Transaction log, a chronological record of data processing *Travel journal, a record of the traveller's experience during the course of their journey In publishing, ''journal'' can refer to various periodicals or serials: *Academic journal, an academic or scholarly periodical **Scientific journal, an academic journal focusing on science **Medical journal, an academic journal focusing on medicine **Law review, a professional journal focusing on legal interpretation *Magazine, non-academic or scho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robert Tibshirani
Robert Tibshirani (born July 10, 1956) is a professor in the Departments of Statistics and Biomedical Data Science at Stanford University. He was a professor at the University of Toronto from 1985 to 1998. In his work, he develops statistical tools for the analysis of complex datasets, most recently in genomics and proteomics. His most well-known contributions are the Lasso method, which proposed the use of L1 penalization in regression and related problems, and Significance Analysis of Microarrays. Education and early life Tibshirani was born on 10 July 1956 in Niagara Falls, Ontario, Canada. He received his B. Math. in statistics and computer science from the University of Waterloo in 1979 and a Master's degree in Statistics from the University of Toronto in 1980. Tibshirani joined the doctoral program at Stanford University in 1981 and received his Ph.D. in 1984 under the supervision of Bradley Efron. His dissertation was entitled "Local likelihood estimation". Honors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lasso Regression
In statistics and machine learning, lasso (least absolute shrinkage and selection operator; also Lasso, LASSO or L1 regularization) is a regression analysis method that performs both variable selection and regularization in order to enhance the prediction accuracy and interpretability of the resulting statistical model. The lasso method assumes that the coefficients of the linear model are sparse, meaning that few of them are non-zero. It was originally introduced in geophysics, and later by Robert Tibshirani, who coined the term. Lasso was originally formulated for linear regression models. This simple case reveals a substantial amount about the estimator. These include its relationship to ridge regression and best subset selection and the connections between lasso coefficient estimates and so-called soft thresholding. It also reveals that (like standard linear regression) the coefficient estimates do not need to be unique if covariates are collinear. Though originally defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
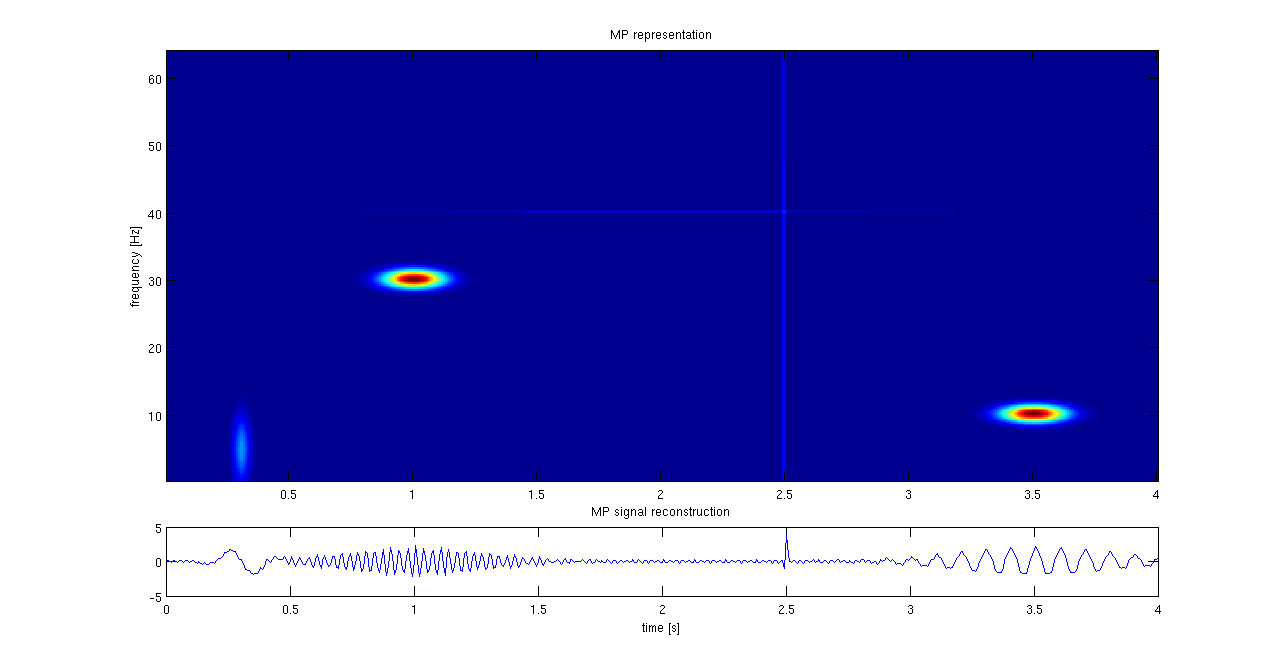
Matching Pursuit
Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete (i.e., redundant) dictionary D. The basic idea is to approximately represent a signal f from Hilbert space H as a weighted sum of finitely many functions g_ (called atoms) taken from D. An approximation with N atoms has the form : f(t) \approx \hat f_N(t) := \sum_^ a_n g_(t) where g_ is the \gamma_nth column of the matrix D and a_n is the scalar weighting factor (amplitude) for the atom g_. Normally, not every atom in D will be used in this sum. Instead, matching pursuit chooses the atoms one at a time in order to maximally (greedily) reduce the approximation error. This is achieved by finding the atom that has the highest inner product with the signal (assuming the atoms are normalized), subtracting from the signal an approximation that uses only that one atom, and repeating the process until the signal is satisfactoril ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Statistics
Robust statistics are statistics that maintain their properties even if the underlying distributional assumptions are incorrect. Robust Statistics, statistical methods have been developed for many common problems, such as estimating location parameter, location, scale parameter, scale, and regression coefficient, regression parameters. One motivation is to produce statistical methods that are not unduly affected by outliers. Another motivation is to provide methods with good performance when there are small departures from a Parametric statistics, parametric distribution. For example, robust methods work well for mixtures of two normal distributions with different standard deviations; under this model, non-robust methods like a t-test work poorly. Introduction Robust statistics seek to provide methods that emulate popular statistical methods, but are not unduly affected by outliers or other small departures from Statistical assumption, model assumptions. In statistics, classical e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Median-unbiased Estimator
The median of a set of numbers is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. For a data set, it may be thought of as the “middle" value. The basic feature of the median in describing data compared to the mean (often simply described as the "average") is that it is not skewed by a small proportion of extremely large or small values, and therefore provides a better representation of the center. Median income, for example, may be a better way to describe the center of the income distribution because increases in the largest incomes alone have no effect on the median. For this reason, the median is of central importance in robust statistics. Median is a 2-quantile; it is the value that partitions a set into two equal parts. Finite set of numbers The median of a finite list of numbers is the "middle" number, when those numbers are listed in order from smallest to greatest. If the data set has an odd numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George W
George Walker Bush (born July 6, 1946) is an American politician and businessman who was the 43rd president of the United States from 2001 to 2009. A member of the Bush family and the Republican Party (United States), Republican Party, he is the eldest son of the 41st president, George H. W. Bush, and was the 46th governor of Texas from 1995 to 2000. Bush flew warplanes in the Texas Air National Guard in his twenties. After graduating from Harvard Business School in 1975, he worked in the oil industry. He later co-owned the Major League Baseball team Texas Rangers (baseball), Texas Rangers before being elected governor of Texas 1994 Texas gubernatorial election, in 1994. Governorship of George W. Bush, As governor, Bush successfully sponsored legislation for tort reform, increased education funding, set higher standards for schools, and reformed the criminal justice system. He also helped make Texas the Wind power in Texas, leading producer of wind-generated electricity in t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |