|
Clock (model Checking)
In model checking, a subfield of computer science, a clock is a mathematical object used to model time. More precisely, a clock measures how much time passed since a particular event occurs, in this sense, a clock is more precisely an abstraction of a stopwatch. In a model of some particular program, the value of the clock may either be the time since the program was started, or the time since a particular event occurred in the program. Those clocks are used in the definition of timed automaton, signal automaton, timed propositional temporal logic and clock temporal logic. They are also used in programs such as UPPAAL which implement timed automata. Generally, the model of a system uses many clocks. Those multiple clocks are required in order to track a bounded number of events. All of those clocks are synchronized. That means that the difference in value between two fixed clocks is constant until one of them is restarted. In the language of electronics, it means that clock's jitte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Model Checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software systems, where the specification contains liveness requirements (such as avoidance of livelock) as well as safety requirements (such as avoidance of states representing a system crash). In order to solve such a problem algorithmically, both the model of the system and its specification are formulated in some precise mathematical language. To this end, the problem is formulated as a task in logic, namely to check whether a structure satisfies a given logical formula. This general concept applies to many kinds of logic and many kinds of structures. A simple model-checking problem consists of verifying whether a formula in the propositional logic is satisfied by a given structure. Overview Property checking is used for verification when two ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logical Conjunction
In logic, mathematics and linguistics, ''and'' (\wedge) is the Truth function, truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as \wedge or \& or K (prefix) or \times or \cdot in which \wedge is the most modern and widely used. The ''and'' of a set of operands is true if and only if ''all'' of its operands are true, i.e., A \land B is true if and only if A is true and B is true. An operand of a conjunction is a conjunct. Beyond logic, the term "conjunction" also refers to similar concepts in other fields: * In natural language, the denotation of expressions such as English language, English "Conjunction (grammar), and"; * In programming languages, the Short-circuit evaluation, short-circuit and Control flow, control structure; * In set theory, Intersection (set theory), intersection. * In Lattice (order), lattice theory, logical conjunction (Infimum and supremum, greatest lower bound). Notati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Timed Propositional Temporal Logic
In model checking, a field of computer science, timed propositional temporal logic (TPTL) is an extension of propositional linear temporal logic (LTL) in which variables are introduced to measure times between two events. For example, while LTL allows to state that each event ''p'' is eventually followed by an event ''q'', TPTL furthermore allows to give a time limit for ''q'' to occur. Syntax The future fragment of TPTL is defined similarly to linear temporal logic, in which furthermore, clock variables can be introduced and compared to constants. Formally, given a set X of clocks, is built up from: * a finite set of propositional variables ''AP'', * the logical operators ¬ and ∨, and * the temporal modal operator U, * a clock comparison x\sim c, with x\in X, c a number and \sim a comparison operator such as <, ≤, =, ≥ or >. * a freeze quantification operator x.\phi, for \phi a TPTL formula with set of clocks X\cup\. Furthermore, for I=(a,b) an interval, x\in I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Clock Temporal Logic
A clock or chronometer is a device that measures and displays time. The clock is one of the oldest human inventions, meeting the need to measure intervals of time shorter than the natural units such as the day, the lunar month, and the year. Devices operating on several physical processes have been used over the millennia. Some predecessors to the modern clock may be considered "clocks" that are based on movement in nature: A sundial shows the time by displaying the position of a shadow on a flat surface. There is a range of duration timers, a well-known example being the hourglass. Water clocks, along with sundials, are possibly the oldest time-measuring instruments. A major advance occurred with the invention of the verge escapement, which made possible the first mechanical clocks around 1300 in Europe, which kept time with oscillating timekeepers like balance wheels., pp. 103–104., p. 31. Traditionally, in horology (the study of timekeeping), the term ''clock'' was us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
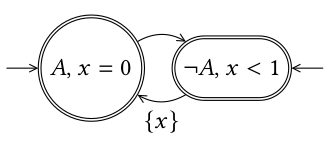
Signal Automaton
In automata theory, a field of computer science, a signal automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a signal automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Example Before formally defining what a signal automaton is, an example will be given. Let one consider the language \mathcal L of signals, over a binary alphabet \, which contains signals \gamma such that: * A appears in singular intervals. That is, the set of times \ is discrete, and * A appears at least once during each interval of length one. This language can be accepted by the automaton pictured nearby. As for finite automaton, incoming arrows represents initial locations and double circle represents accepting l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Timed Automaton
timed (time daemon) is an operating system program that maintains the system time in synchronization with time servers using the Time Synchronization Protocol (TSP) developed by Riccardo Gusella and Stefano Zatti. Gusella and Zatti had done earlier related work on their TEMPO algorithm. The Time Synchronization Protocol specification refers to an election algorithm and a synchronization mechanism specified in other technical reports listed as "to appear". With the release of macOS High Sierra in 2017, timed in macOS has subsumed all time synchronization responsibilities including those of the former ntpd and timed. See also * Network Time Protocol (NTP) * Precision Time Protocol (IEEE 1588 PTP) References External links timed(8) man page* ', System Manager's Manual (SMM:11) * ', System Manager's Manual (SMM:12) Network time-related software {{operating-system-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Region (model Checking)
In model checking, a field of computer science, a region is a convex polytope in \mathbb R^d for some dimension d, and more precisely a zone, satisfying some minimality property. The regions partition \mathbb R^d. The set of zones depends on a set K of constraints of the form x\le c, x\ge c, x_1\le x_2+c and x_1\ge x_2+c, with x_1 and x_2 some variables, and c a constant. The regions are defined such that if two vectors \vec x and \vec x' belong to the same region, then they satisfy the same constraints of K. Furthermore, when those vectors are considered as a tuple of clocks, both vectors have the same set of possible futures. Intuitively, it means that any timed propositional temporal logic-formula, or timed automaton or signal automaton using only the constraints of K can not distinguish both vectors. The set of region allows to create the region automaton, which is a directed graph in which each node is a region, and each edge r\to r' ensure that r' is a possible future of r. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Difference Bound Matrix
In model checking, a field of computer science, a difference bound matrix (DBM) is a data structure used to represent some convex polytopes called zones. This structure can be used to efficiently implement some geometrical operations over zones, such as testing emptyness, inclusion, equality, and computing the intersection and the sum of two zones. It is, for example, used in the Uppaal model checker; where it is also distributed as an independent library. More precisely, there is a notion of canonical DBM; there is a one-to-one relation between canonical DBMs and zones and from each DBM a canonical equivalent DBM can be efficiently computed. Thus, equality of zone can be tested by checking for equality of canonical DBMs. Zone A difference bound matrix is used to represents some kind of convex polytopes. Those polytopes are called zone. They are now defined. Formally, a zone is defined by equations of the form x\le c, x\ge c, x_1\le x_2+c and x_1\ge x_2+c, with x_1 and x_2 some ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
First-order Logic
First-order logic, also called predicate logic, predicate calculus, or quantificational logic, is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables. Rather than propositions such as "all humans are mortal", in first-order logic one can have expressions in the form "for all ''x'', if ''x'' is a human, then ''x'' is mortal", where "for all ''x"'' is a quantifier, ''x'' is a variable, and "... ''is a human''" and "... ''is mortal''" are predicates. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic. A theory about a topic, such as set theory, a theory for groups,A. Tarski, ''Undecidable Theories'' (1953), p. 77. Studies in Logic and the Foundation of Mathematics, North-Holland or a formal theory o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jitter
In electronics and telecommunications, jitter is the deviation from true periodicity of a presumably periodic signal, often in relation to a reference clock signal. In clock recovery applications it is called timing jitter. Jitter is a significant, and usually undesired, factor in the design of almost all communications links. Jitter can be quantified in the same terms as all time-varying signals, e.g., root mean square (RMS), or peak-to-peak displacement. Also, like other time-varying signals, jitter can be expressed in terms of spectral density. Jitter period is the interval between two times of maximum effect (or minimum effect) of a signal characteristic that varies regularly with time. Jitter frequency, the more commonly quoted figure, is its inverse. ITU-T G.810 classifies deviation lower frequencies below 10 Hz as ''wander'' and higher frequencies at or above 10 Hz as ''jitter''. Jitter may be caused by electromagnetic interference and crosstalk with ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |