|
Classification Of Electromagnetic Fields
In differential geometry and theoretical physics, the classification of electromagnetic fields is a pointwise classification of bivectors at each point of a Lorentzian manifold. It is used in the study of solutions of Maxwell's equations and has applications in Einstein's theory of relativity. The classification theorem The electromagnetic field at a point ''p'' (i.e. an event) of a Lorentzian spacetime is represented by a real bivector defined over the tangent space at ''p''. The tangent space at ''p'' is isometric as a real inner product space to E1,3. That is, it has the same notion of vector magnitude and angle as Minkowski spacetime. To simplify the notation, we will assume the spacetime ''is'' Minkowski spacetime. This tends to blur the distinction between the tangent space at ''p'' and the underlying manifold; fortunately, nothing is lost by this specialization, for reasons we discuss as the end of the article. The classification theorem for electromagnetic fields chara ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Rank (linear Algebra)
In linear algebra, the rank of a matrix (mathematics), matrix is the Dimension (vector space), dimension of the vector space generated (or Linear span, spanned) by its columns. p. 48, § 1.16 This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the "Degenerate form, nondegenerateness" of the system of linear equations and linear transformation encoded by . There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics. The rank is commonly denoted by or ; sometimes the parentheses are not written, as in .Alternative notation includes \rho (\Phi) from and . Main definitions In this section, we give some definitions of the rank of a matrix. Many definitions are possible; see #Alternative definitions, Alternative definitions for several of these. The column rank of is the dimension (linear alg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Lorentz Group
In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz. For example, the following laws, equations, and theories respect Lorentz symmetry: * The kinematical laws of special relativity * Maxwell's field equations in the theory of electromagnetism * The Dirac equation in the theory of the electron * The Standard Model of particle physics The Lorentz group expresses the fundamental symmetry of space and time of all known fundamental laws of nature. In small enough regions of spacetime where gravitational variances are negligible, physical laws are Lorentz invariant in the same manner as special relativity. Basic properties The Lorentz group is a subgroup of the Poincaré group—the group of all isometries of Minkowski spacetime. Lorentz transformations are, pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Electrovacuum Solution
In general relativity, an electrovacuum solution (electrovacuum) is an exact solution of the Einstein field equation in which the only nongravitational mass–energy present is the field energy of an electromagnetic field, which must satisfy the (curved-spacetime) ''source-free'' Maxwell equations appropriate to the given geometry. For this reason, electrovacuums are sometimes called (source-free) ''Einstein–Maxwell solutions''. Definition In general relativity, the geometric setting for physical phenomena is a Lorentzian manifold, which is interpreted as a curved spacetime, and which is specified by defining a metric tensor g_ (or by defining a frame field). The Riemann curvature tensor R_ of this manifold and associated quantities such as the Einstein tensor G^, are well-defined. In general relativity, they can be interpreted as geometric manifestations (curvature and forces) of the gravitational field. We also need to specify an electromagnetic field by defining an ele ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Electromagnetic Peeling Theorem
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electricity and magnetism, two distinct but closely intertwined phenomena. In essence, electric forces occur between any two charged particles, causing an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs exclusively between ''moving'' charged particles. These two effects combine to create electromagnetic fields in the vicinity of charge particles, which can exert influence on other particles via the Lorentz force. At high energy, the weak force and electromagnetic force are unified as a single electroweak force. The electromagnetic force is responsible for many of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Frame Fields In General Relativity
A frame field in general relativity (also called a tetrad or vierbein) is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by \vec_0 and the three spacelike unit vector fields by \vec_1, \vec_2, \, \vec_3. All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field. Frame were introduced into general relativity by Albert Einstein in 1928 and by Hermann Weyl in 1929.Hermann Weyl "Elektron und Gravitation I", ''Zeitschrift Physik'', 56, p330–352, 1929. The index notation for tetrads is explained in tetrad (index notation). Physical interpretation Frame fields of a Lorentzian manifold always correspond to a family of ideal observers immersed in the given spacetime; the integral curves of the timelike unit vector field are the worldlines of these obser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Inertial Frame Of Reference
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. It is a frame in which an isolated physical object — an object with zero net force acting on it — is perceived to move with a constant velocity (it might be a zero velocity) or, equivalently, it is a frame of reference in which Newton's first law of motion holds. All inertial frames are in a state of constant, rectilinear motion with respect to one another; in other words, an accelerometer moving with any of them would detect zero acceleration. It has been observed that celestial objects which are far away from other objects and which are in uniform motion with respect to the cosmic microwave background radiation maintain such uniform motion. Measurements in one inertial frame can be converted to measurements in another by a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Plane Wave
In physics, a plane wave is a special case of wave or field: a physical quantity whose value, at any moment, is constant through any plane that is perpendicular to a fixed direction in space. For any position \vec x in space and any time t, the value of such a field can be written as :F(\vec x,t) = G(\vec x \cdot \vec n, t), where \vec n is a unit-length vector, and G(d,t) is a function that gives the field's value as dependent on only two real parameters: the time t, and the scalar-valued displacement d = \vec x \cdot \vec n of the point \vec x along the direction \vec n. The displacement is constant over each plane perpendicular to \vec n. The values of the field F may be scalars, vectors, or any other physical or mathematical quantity. They can be complex numbers, as in a complex exponential plane wave. When the values of F are vectors, the wave is said to be a longitudinal wave if the vectors are always collinear with the vector \vec n, and a transverse wave if t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Minkowski Metric
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invariant. Because ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Index Gymnastics
In mathematics and mathematical physics, raising and lowering indices are operations on tensors which change their type. Raising and lowering indices are a form of index manipulation in tensor expressions. Vectors, covectors and the metric Mathematical formulation Mathematically vectors are elements of a vector space V over a field K, and for use in physics V is usually defined with K=\mathbb or \mathbb. Concretely, if the dimension n=\text(V) of V is finite, then, after making a choice of basis, we can view such vector spaces as \mathbb^n or \mathbb^n. The dual space is the space of linear functionals mapping V\rightarrow K. Concretely, in matrix notation these can be thought of as row vectors, which give a number when applied to column vectors. We denote this by V^*:= \text(V,K), so that \alpha \in V^* is a linear map \alpha:V\rightarrow K. Then under a choice of basis \, we can view vectors v\in V as an K^n vector with components v^i (vectors are taken by convention to have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Geometrized Unit System
A geometrized unit system, geometric unit system or geometrodynamic unit system is a system of natural units in which the base physical units are chosen so that the speed of light in vacuum, ''c'', and the gravitational constant, ''G'', are set equal to unity. : c = 1 \ : G = 1 \ The geometrized unit system is not a completely defined system. Some systems are geometrized unit systems in the sense that they set these, in addition to other constants, to unity, for example Stoney units and Planck units. This system is useful in physics, especially in the special and general theories of relativity. All physical quantities are identified with geometric quantities such as areas, lengths, dimensionless numbers, path curvatures, or sectional curvatures. Many equations in relativistic physics appear simpler when expressed in geometric units, because all occurrences of ''G'' and of ''c'' drop out. For example, the Schwarzschild radius of a nonrotating uncharged black hole with mas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
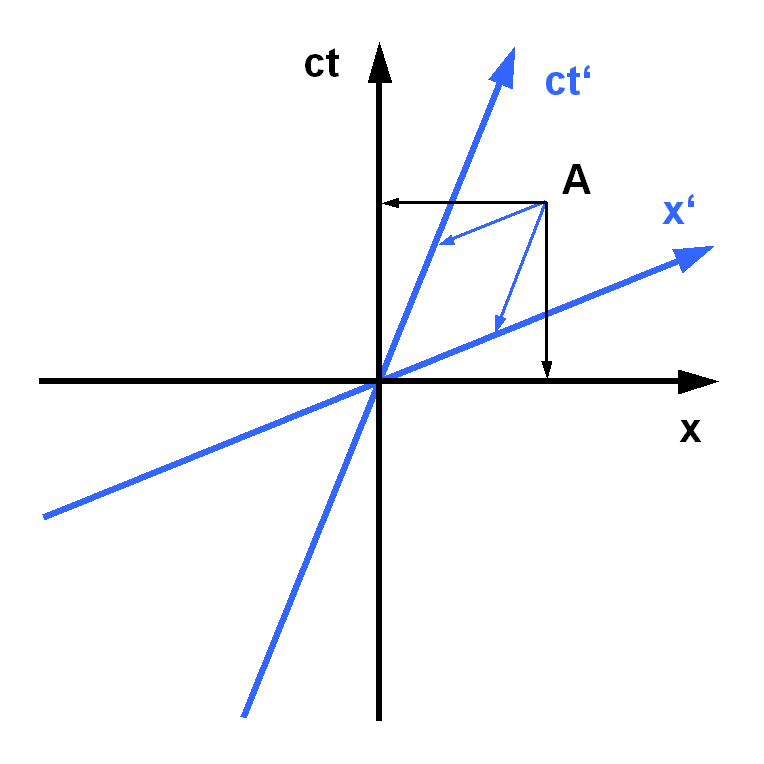Minkowski Space
In mathematical physics, Minkowski space (or Minkowski spacetime) () is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be implied by the postulates of special relativity. Minkowski space is closely associated with Einstein's theories of special relativity and general relativity and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.This makes spacetime distance an invarian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |