|
Chromatic (other)
Chromatic, a word ultimately derived from the Greek noun χρῶμα (''khrṓma''), which means "complexion" or "color", and then from the Greek adjective χρωματικός (''khrōmatikós''; "colored"), may refer to: In music *Chromatic scale, the western-tempered twelve-tone scale *Chromatic chord, chords built from tones chromatically altered from the native scale of the musical composition *Chromaticism, the use of chromatic scales, chords, and modulations * Total chromatic, the use of all twelve pitches of the chromatic scale in tonal music * Chromatic fantasia, a specific form of fantasia originating in sixteenth century Europe *The Chromatic button accordion *The chromatic harmonica *Chromatic genus, a genus of divisions of the tetrachord characterized by an upper interval of a minor third *Diatonic and chromatic, as a property of several structures, genres, and other features in music, often contrasted with ''diatonic'' *Chromatics (band), an American electronic music ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Scale
The chromatic scale (or twelve-tone scale) is a set of twelve pitches (more completely, pitch classes) used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano. Most music uses subsets of the chromatic scale such as diatonic scales. While the chromatic scale is fundamental in western music theory, it is seldom directly used in its entirety in musical compositions or improvisation. Definition The chromatic scale is a musical scale with twelve pitches, each a semitone, also known as a half-step, above or below its adjacent pitches. As a result, in 12-tone equal temperament (the most common tuning in Western music), the chromatic scale covers all 12 of the available pitches. Thus, there is only one chromatic scal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
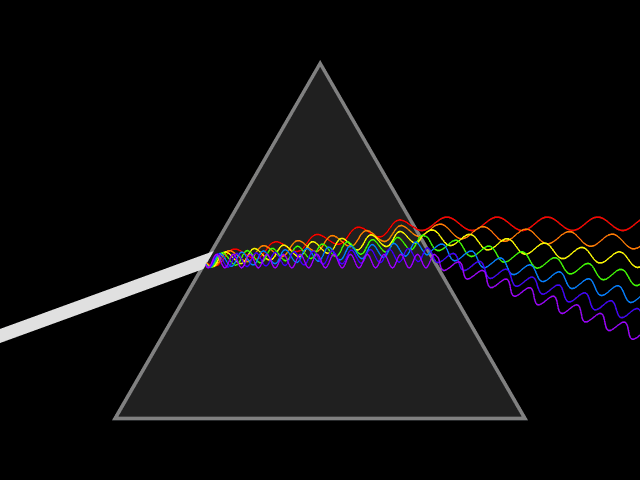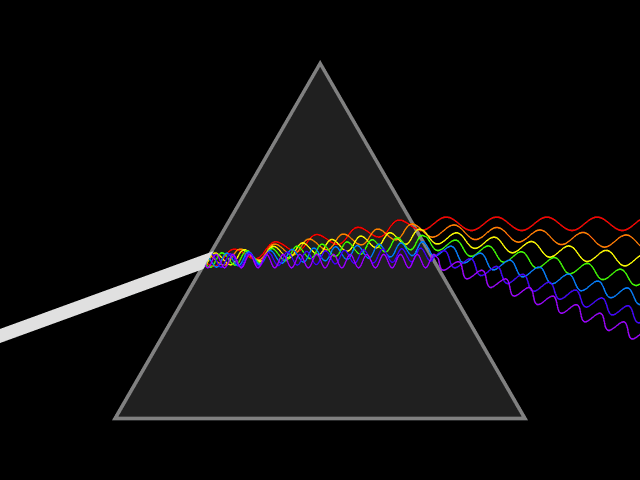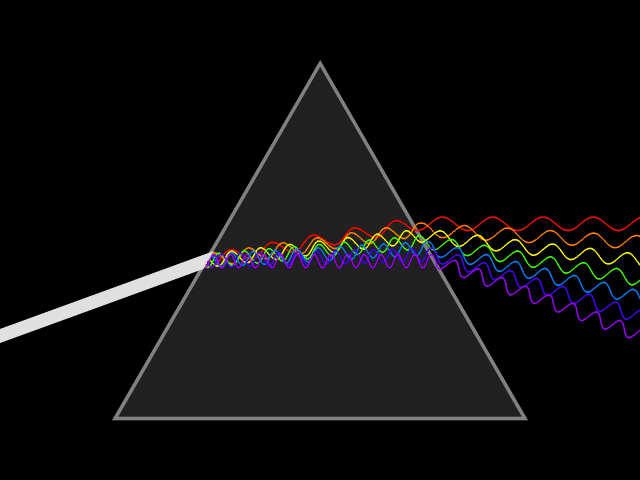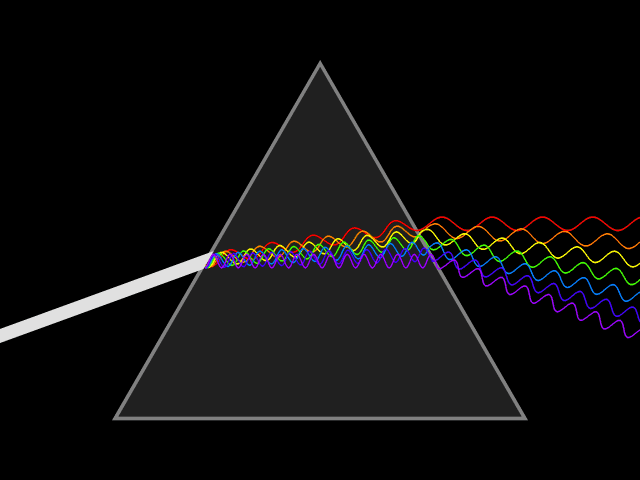
Dispersion (optics)
Dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency. Sometimes the term chromatic dispersion is used to refer to optics specifically, as opposed to wave propagation in general. A medium having this common property may be termed a dispersive medium. Although the term is used in the field of optics to describe light and other electromagnetic waves, dispersion in the same sense can apply to any sort of wave motion such as acoustic dispersion in the case of sound and seismic waves, and in gravity waves (ocean waves). Within optics, dispersion is a property of telecommunication signals along transmission lines (such as microwaves in coaxial cable) or the Pulse (signal processing), pulses of light in optical fiber. In optics, one important and familiar consequence of dispersion is the change in the angle of refraction of different colors of light, as seen in the spectrum produced by a dispersive Prism (optics), prism and in chromatic aberration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatics Inc
Chromatic, a word ultimately derived from the Greek noun χρῶμα (''khrṓma''), which means "complexion" or "color", and then from the Greek adjective χρωματικός (''khrōmatikós''; "colored"), may refer to: In music *Chromatic scale, the western-tempered twelve-tone scale *Chromatic chord, chords built from tones chromatically altered from the native scale of the musical composition *Chromaticism, the use of chromatic scales, chords, and modulations *Total chromatic, the use of all twelve pitches of the chromatic scale in tonal music *Chromatic fantasia, a specific form of fantasia originating in sixteenth century Europe *The Chromatic button accordion *The Harmonica#Chromatic, chromatic harmonica *Chromatic genus, a genus of divisions of the tetrachord characterized by an upper interval of a minor third *Diatonic and chromatic, as a property of several structures, genres, and other features in music, often contrasted with ''diatonic'' *Chromatics (band), an America ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic (programmer)
Chromatic is a writer and free software programmer best known for his work in the Perl programming language. He lives in Hillsboro, Oregon, United States. He wrote ''Extreme Programming Pocket Guide and the lead author of Perl Hacks'' , co-wrote ''Perl Testing: A Developer's Notebook'', and is an uncredited contributor to ''The Art of Agile Development''. He has a music degree. Also, he has contributed to CPAN, Perl 5, Perl 6, and Parrot. In 2009, he founded Modern Perl Books, in part to revitalize the world of Perl and to publish materials that other publishers had neglected. In 2010, he released the book ''Modern Perl'' in print and in electronic form, with the latter redistributable freely (though with a suggested donation). An updated edition was released in 2012, with the entire text online. CPAN While he may be currently known for the module "Modern::Perl", Chromatic originally wrote "Test::Builder", which is the foundation of most testing in the Perl world. Perl 6 Ch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Dragon
In the ''Dungeons & Dragons'' (''D&D'') fantasy role-playing game, dragons are an iconic type of monstrous creature. As a group, ''D&D'' dragons are loosely based on dragons from a wide range of fictional and mythological sources. ''Dungeons & Dragons'' allows players to fight the fictional dragons in the game (Tiamat being one of the most notable) and "slay their psychic dragons" as well. These dragons, specifically their "dungeon ecology", have implications for the literary theory of fantasy writing. ''D&D'' dragons also featured as targets of the moral panic surrounding the game. In ''D&D'', dragons are depicted as any of various species of large, intelligent, magical, reptilian beasts, each typically defined by a combination of their demeanor and either the color of their scales or their elemental affinity. For example, a commonly presented species of dragon is the red dragon, which is named for its red scales, and known for its evil and greedy nature, as well as its abilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Luschan's Chromatic Scale
The term () is used in German surnames either as a nobiliary particle indicating a noble patrilineality, or as a simple preposition used by commoners that means or . Nobility directories like the often abbreviate the noble term to ''v.'' In medieval or early modern names, the particle was at times added to commoners' names; thus, meant . This meaning is preserved in Swiss toponymic surnames and in the Dutch , which is a cognate of but also does not necessarily indicate nobility. Usage Germany and Austria The abolition of the monarchies in Germany and Austria in 1919 meant that neither state has a privileged nobility, and both have exclusively republican governments. In Germany, this means that legally ''von'' simply became an ordinary part of the surnames of the people who used it. There are no longer any legal privileges or constraints associated with this naming convention. According to German alphabetical sorting, people with ''von'' in their surnames – of nob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex Chromatic Number
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an '' edge coloring'' assigns a color to each edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Chromatic Number
Fractional coloring is a topic in a branch of graph theory known as fractional graph theory. It is a generalization of ordinary graph coloring. In a traditional graph coloring, each vertex in a graph is assigned some color, and adjacent vertices — those connected by edges — must be assigned different colors. In a fractional coloring however, a ''set'' of colors is assigned to each vertex of a graph. The requirement about adjacent vertices still holds, so if two vertices are joined by an edge, they must have no colors in common. Fractional graph coloring can be viewed as the linear programming relaxation of traditional graph coloring. Indeed, fractional coloring problems are much more amenable to a linear programming approach than traditional coloring problems. Definitions A ''b''-fold coloring of a graph ''G'' is an assignment of sets of size ''b'' to vertices of a graph such that adjacent vertices receive disjoint sets. An ''a'':''b''-coloring is a ''b''-fold coloring out ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strong Chromatic Number
In graph theory, a strong coloring, with respect to a partition of the vertices into (disjoint) subsets of equal sizes, is a (proper) vertex coloring in which every color appears exactly once in every part. A graph is strongly ''k''-colorable if, for each partition of the vertices into sets of size ''k'', it admits a strong coloring. When the order of the graph ''G'' is not divisible by ''k'', we add isolated vertices to ''G'' just enough to make the order of the new graph ' divisible by ''k''. In that case, a strong coloring of ' minus the previously added isolated vertices is considered a strong coloring of ''G''. The strong chromatic number sχ(''G'') of a graph ''G'' is the least ''k'' such that ''G'' is strongly ''k''-colorable. A graph is strongly ''k''-chromatic if it has strong chromatic number ''k''. Some properties of sχ(''G''): # sχ(''G'') > Δ(''G''). # sχ(''G'') ≤ 3 Δ(''G'') − 1. # Asymptotically, sχ(''G'') ≤ 11 Δ(''G'') / 4 + o(Δ(''G'')). Here, � ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acyclic Chromatic Number
In graph theory, an acyclic coloring is a (proper) vertex coloring in which every 2-chromatic subgraph is acyclic. The acyclic chromatic number of a graph is the fewest colors needed in any acyclic coloring of . Acyclic coloring is often associated with graphs embedded on non-plane surfaces. Upper bounds A(''G'') ≤ 2 if and only if ''G'' is acyclic. Bounds on A(''G'') in terms of Δ(''G''), the maximum degree of ''G'', include the following: * A(''G'') ≤ 4 if Δ(''G'') = 3. * A(''G'') ≤ 5 if Δ(''G'') = 4. * A(''G'') ≤ 7 if Δ(''G'') = 5. * A(''G'') ≤ 12 if Δ(''G'') = 6. A milestone in the study of acyclic coloring is the following affirmative answer to a conjecture of Grünbaum: :Theorem A(''G'') ≤ 5 if ''G'' is planar graph. introduced acyclic coloring and acyclic chromatic number, and conjectured the result in the above theorem. Borodin's proof involved several years of painstaking inspection of 450 reducible configurations. One consequence of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chromatic Index
In graph theory, a proper edge coloring of a Graph (discrete mathematics), graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most different colors, for a given value of , or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three. By Vizing's theorem, the number of colors needed to edge color a simple graph is either its maximum Degree (graph theory), degree or . For some graphs, such as bip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Coloring
In graph theory, graph coloring is a methodic assignment of labels traditionally called "colors" to elements of a Graph (discrete mathematics), graph. The assignment is subject to certain constraints, such as that no two adjacent elements have the same color. Graph coloring is a special case of graph labeling. In its simplest form, it is a way of coloring the Vertex (graph theory), vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an ''edge coloring'' assigns a color to each Edge (graph theory), edges so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each Face (graph theory), face (or region) so that no two faces that share a boundary have the same color. Vertex coloring is often used to introduce graph coloring problems, since other coloring problems can be transformed into a vertex coloring instance. For example, an edge coloring of a graph is just ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |