|
Cavalieri's Quadrature Formula
In calculus, Cavalieri's quadrature formula, named for 17th-century Italian mathematician Bonaventura Cavalieri, is the integral :\int_0^a x^n\,dx = \tfrac\, a^ \qquad n \geq 0, and generalizations thereof. This is the definite integral form; the indefinite integral form is: :\int x^n\,dx = \tfrac\, x^ + C \qquad n \neq -1. There are additional forms, listed below. Together with the linearity of the integral, this formula allows one to compute the integrals of all polynomials. The term " quadrature" is a traditional term for area; the integral is geometrically interpreted as the area under the curve ''y'' = ''x''''n''. Traditionally important cases are ''y'' = ''x''2, the quadrature of the parabola, known in antiquity, and ''y'' = 1/''x'', the quadrature of the hyperbola, whose value is a logarithm. Forms Negative ''n'' For negative values of ''n'' (negative powers of ''x''), there is a singularity at ''x'' = 0, and thus the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
X Cubed Plot
X, or x, is the twenty-fourth letter of the Latin alphabet, used in the modern English alphabet, the alphabets of other western European languages and others worldwide. Its name in English is ''ex'' (pronounced ), plural ''exes''."X", ''Oxford English Dictionary'', 2nd edition (1989); ''Merriam-Webster's Third New International Dictionary of the English Language, Unabridged'' (1993); "ex", ''op. cit''. History The letter , representing , was inherited from the Etruscan alphabet. It perhaps originated in the of the Euboean alphabet or another Western Greek alphabet, which also represented . Its relationship with the of the Eastern Greek alphabets, which represented , is uncertain. The pronunciation of in the Romance languages underwent sound changes, with various outcomes: * French: (e.g. ''laisser'' from ''laxare'') * Italian: (e.g. ''asse'' from ''axem'') and, in some cases, (e.g. ''lasciare'' from ''laxare'') * Portuguese: (e.g. ''eixo'' from ''axem'') ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covering Space
In topology, a covering or covering projection is a continuous function, map between topological spaces that, intuitively, Local property, locally acts like a Projection (mathematics), projection of multiple copies of a space onto itself. In particular, coverings are special types of local homeomorphisms. If p : \tilde X \to X is a covering, (\tilde X, p) is said to be a covering space or cover of X, and X is said to be the base of the covering, or simply the base. By abuse of terminology, \tilde X and p may sometimes be called covering spaces as well. Since coverings are local homeomorphisms, a covering space is a special kind of étalé space. Covering spaces first arose in the context of complex analysis (specifically, the technique of analytic continuation), where they were introduced by Bernhard Riemann, Riemann as domains on which naturally multivalued function, multivalued complex functions become single-valued. These spaces are now called Riemann surfaces. Covering spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in ''n'' dimensions is equal to \sqrt. An ''n''-dimensional hypercube is more commonly referred to as an ''n''-cube or sometimes as an ''n''-dimensional cube. The term measure polytope (originally from Elte, 1912) is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes. The hypercube is the special case of a hyperrectangle (also called an ''n-orthotope''). A ''unit hypercube'' is a hypercube whose side has length one unit. Often, the hypercube whose corners (or ''vertices'') are the 2''n'' points in R''n'' with each coordinate equal to 0 or 1 i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Candidate Solution
In mathematical optimization and computer science, a feasible region, feasible set, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down. For example, consider the problem of minimizing the function x^2+y^4 with respect to the variables x and y, subject to 1 \le x \le 10 and 5 \le y \le 12. \, Here the feasible set is the set of pairs (''x'', ''y'') in which the value of ''x'' is at least 1 and at most 10 and the value of ''y'' is at least 5 and at most 12. The feasible set of the problem is separate from the objective function, which states the criterion to be optimized and which in the above example is x^2+y^4. In many problems, the feasible set reflects a constraint that on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, veloc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Calculus
The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, integrating a function (calculating the area under its graph, or the cumulative effect of small contributions). Roughly speaking, the two operations can be thought of as inverses of each other. The first part of the theorem, the first fundamental theorem of calculus, states that for a continuous function , an antiderivative or indefinite integral can be obtained as the integral of over an interval with a variable upper bound. Conversely, the second part of the theorem, the second fundamental theorem of calculus, states that the integral of a function over a fixed Interval (mathematics), interval is equal to the change of any antiderivative between the ends of the interval. This greatly simplifies the calculation of a definite integral pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Definition Of The Derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the instantaneous rate of change, the ratio of the instantaneous change in the dependent variable to that of the independent variable. The process of finding a derivative is called differentiation. There are multiple different notations for differentiation. ''Leibniz notation'', named after Gottfried Wilhelm Leibniz, is represented as the ratio of two differentials, whereas ''prime notation'' is written by adding a prime mark. Higher order notations represent repeated differentiation, and they are usually denoted in Leibniz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Formula
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and are nonnegative integers satisfying and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in each term is known as the binomial coefficient or (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where gives the number of different combinations (i.e. subsets) of elements that can be chosen from an -element set. Therefore is usually pronounced as " choose ". Statement According to the theorem, the expansion of any nonnegative integer power of the binomial is a sum of the form (x+y)^n = x^n y^0 + x^ y^1 + x^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Principal Value
In mathematics, the Cauchy principal value, named after Augustin-Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined. In this method, a singularity on an integral interval is avoided by limiting the integral interval to the non singular domain. Formulation Depending on the type of singularity in the integrand , the Cauchy principal value is defined according to the following rules: In some cases it is necessary to deal simultaneously with singularities both at a finite number and at infinity. This is usually done by a limit of the form \lim_\, \lim_ \,\left ,\int_^ f(x)\,\mathrmx \,~ + ~ \int_^ f(x)\,\mathrmx \,\right In those cases where the integral may be split into two independent, finite limits, \lim_ \, \left, \,\int_a^ f(x)\,\mathrmx \,\\; < \;\infty and then the function is integrable in the ordinary sense. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
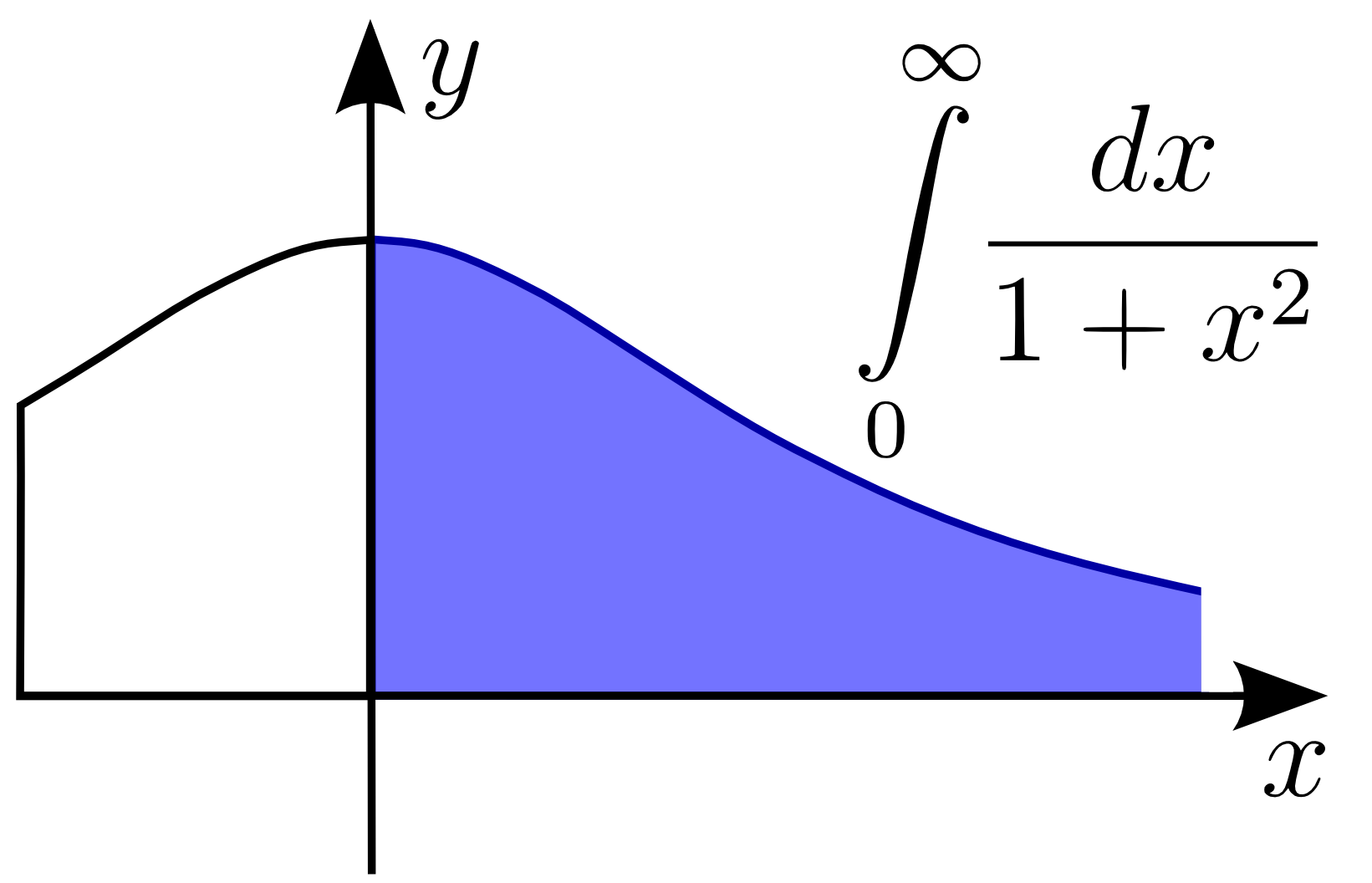
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Function
In mathematics, an even function is a real function such that f(-x)=f(x) for every x in its domain. Similarly, an odd function is a function such that f(-x)=-f(x) for every x in its domain. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = x^n is even if ''n'' is an even integer, and it is odd if ''n'' is an odd integer. Even functions are those real functions whose graph is self-symmetric with respect to the and odd functions are those whose graph is self-symmetric with respect to the origin. If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function. Early history The concept of even and odd functions appears to date back to the early 18th century, with Leonard Euler playing a significant role in their formalization. Euler introduced the concepts of even and odd functions (using Lati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |