|
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-nega ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sedrakyan's Inequality
The following inequality is known as Sedrakyan's inequality, Bergström's inequality, Engel's form or Titu's lemma, respectively, referring to the article ''About the applications of one useful inequality'' of Nairi Sedrakyan published in 1997, to the book ''Problem-solving strategies'' of Arthur Engel published in 1998 and to the book ''Mathematical Olympiad Treasures'' of Titu Andreescu published in 2003. It is a direct consequence of Cauchy–Bunyakovsky–Schwarz inequality. Nevertheless, in his article (1997) Sedrakyan has noticed that written in this form this inequality can be used as a mathematical proof technique and it has very useful new applications. In the book ''Algebraic Inequalities'' (Sedrakyan) are provided several generalizations of this inequality. Statement of the inequality For any reals a_1, a_2, a_3, \ldots, a_n and positive reals b_1, b_2, b_3,\ldots, b_n, we have \frac + \frac + \cdots + \frac \geq \frac. (Nairi Sedrakyan (1997), Arthur Engel (199 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harald Bergström
Harald Bergström (1 April 1908, Mölltorp – 23 May 2001, Göteborg) was a Swedish mathematician, specializing in probability theory. Education and career Harald Bergström studied mathematics, physics and chemistry at the University of Uppsala and received in 1931 his master's degree. From 1932 to 1934 he taught at secondary schools and then worked as a research assistant at the University of Uppsala; there he received his Ph.D. in 1938 and taught until 1945. In 1946 he moved to Chalmers University of Technology in Göteborg, where in 1949 he was appointed a professor of applied mathematics. In 1960 he was also appointed a professor for numerical analysis and mathematical statistics. In 1974 he retired as professor emeritus. At the University of Uppsala, Harald Bergström did research mainly on algebraic number fields and related topics. After his move to Chalmers University of Technology, he focused on probability theory and statistics. He was supervisor to Peter Jagers. He ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
University Of St Andrews
(Aien aristeuein) , motto_lang = grc , mottoeng = Ever to ExcelorEver to be the Best , established = , type = Public research university Ancient university , endowment = £117.7 million (2021) , budget = £286.6 million (2020–21) , chancellor = The Lord Campbell of Pittenweem , rector = Leyla Hussein , principal = Sally Mapstone , academic_staff = 1,230 (2020) , administrative_staff = 1,576 , students = () , undergrad = () , postgrad = () , doctoral = , other = , city = St Andrews , state = , country = Scotland , coordinates = , campus = College town , colours = United College, St Andrews St Mary's College School of Medic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, (if a and b are real, then) the complex conjugate of a + bi is equal to a - bi. The complex conjugate of z is often denoted as \overline or z^*. In polar form, the conjugate of r e^ is r e^. This can be shown using Euler's formula. The product of a complex number and its conjugate is a real number: a^2 + b^2 (or r^2 in polar coordinates). If a root of a univariate polynomial with real coefficients is complex, then its complex conjugate is also a root. Notation The complex conjugate of a complex number z is written as \overline z or z^*. The first notation, a vinculum, avoids confusion with the notation for the conjugate transpose of a matrix, which can be thought of as a generalization of the complex conjugate. The second is preferred in physics, where dagger (†) is used for the conju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fidelity Of Quantum States
In quantum mechanics, notably in quantum information theory, fidelity is a measure of the "closeness" of two quantum states. It expresses the probability that one state will pass a test to identify as the other. The fidelity is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space. Given two density operators \rho and \sigma, the fidelity is generally defined as the quantity F(\rho, \sigma) = \left(\operatorname \sqrt\right)^2. In the special case where \rho and \sigma represent pure quantum states, namely, \rho=, \psi_\rho\rangle\!\langle\psi_\rho, and \sigma=, \psi_\sigma\rangle\!\langle\psi_\sigma, , the definition reduces to the squared overlap between the states: F(\rho, \sigma)=, \langle\psi_\rho, \psi_\sigma\rangle, ^2. While not obvious from the general definition, the fidelity is symmetric: F(\rho,\sigma)=F(\sigma,\rho). Motivation Given two random variables X,Y with values (1, ..., n) ( categorical random varia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
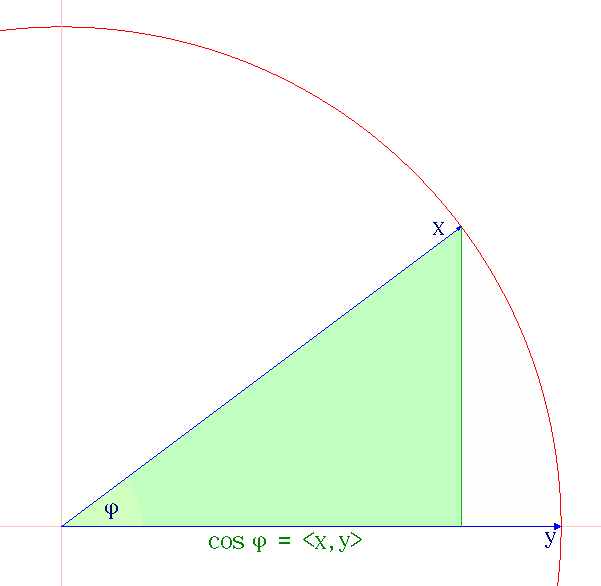
Inner-product Space
In mathematics, an inner product space (or, rarely, a Hausdorff pre-Hilbert space) is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in \langle a, b \rangle. Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality (zero inner product) of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or ''scalar product'' of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898. An inner product naturally induces an associated norm, (denoted , x, and , y, in the picture); ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Numbers
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set endowed with a structure, called a ''topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopies. A property that is invariant under such deformations is a topological property. Basic examples of topological properties are: the dimension, which allows distinguishing between a line and a surface; compactness, which allows distinguishing between a line and a circle; connectedne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |