|
Calkin–Wilf Tree
In number theory, the Calkin–Wilf tree is a tree in which the vertices correspond one-to-one to the positive rational numbers. The tree is rooted at the number 1, and any rational number expressed in simplest terms as the fraction has as its two children the numbers and . Every positive rational number appears exactly once in the tree. It is named after Neil Calkin and Herbert Wilf, but appears in other works including Kepler's ''Harmonices Mundi''. The sequence of rational numbers in a breadth-first traversal of the Calkin–Wilf tree is known as the Calkin–Wilf sequence. Its sequence of numerators (or, offset by one, denominators) is Stern's diatomic series, and can be computed by the fusc function. History The Calkin–Wilf tree is named after Neil Calkin and Herbert Wilf, who considered it in a 2000 paper. In a 1997 paper, Jean Berstel and Aldo de Luca called the same tree the ''Raney tree'', since they drew some ideas from a 1973 paper by George N. Raney. Stern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moritz Abraham Stern
Moritz Abraham Stern (29 June 1807 – 30 January 1894) was a German mathematician. Stern became ''Ordinarius'' (full professor) at Göttingen University in 1858, succeeding Carl Friedrich Gauss. Stern was the first Jewish full professor at a German university who attained the position without changing his Jewish religion. Although Carl Gustav Jacobi preceded him (by three decades) as the first Jew to obtain a math professorial chair in Germany, Jacobi's family had converted to Christianity long before then. As a professor, Stern taught Gauss's student Bernhard Riemann. Stern was very helpful to Gotthold Eisenstein in formulating a proof of the quadratic reciprocity theorem. Stern was interested in primes that cannot be expressed as the sum of a prime and twice a square (now known as Stern prime A Stern prime, named for Moritz Abraham Stern, is a prime number that is not the sum of a smaller prime and twice the square of a non zero integer. That is, if for a prime ''q'' th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations ( Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequence
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description. The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, even though we do not have a formula for the ''n''th perfect number. Examples Integer sequences that have their own name include: * Abundant numbers * Baum–Sweet sequence * Bell n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
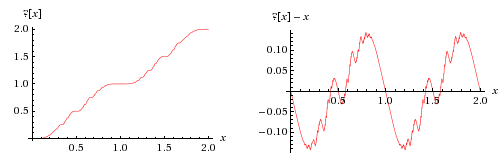
Minkowski's Question Mark Function
In mathematics, the Minkowski question-mark function, denoted , is a function with unusual fractal properties, defined by Hermann Minkowski in 1904. It maps quadratic irrational numbers to rational numbers on the unit interval, via an expression relating the continued fraction expansions of the quadratics to the binary expansions of the rationals, given by Arnaud Denjoy in 1938. It also maps rational numbers to dyadic rationals, as can be seen by a recursive definition closely related to the Stern–Brocot tree. Definition and intuition One way to define the question-mark function involves the correspondence between two different ways of representing fractional numbers using finite or infinite binary sequences. Most familiarly, a string of 0's and 1's with a single point mark ".", like "11.001001000011111..." can be interpreted as the binary representation of a number. In this case this number is 2+1+\frac18+\frac1+\cdots=\pi. There is a different way of interpreting the sam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because \begin -2 \cdot 2 &= -4 \\ 0 \cdot 2 &= 0 \\ 41 \cdot 2 &= 82 \end By contrast, −3, 5, 7, 21 are odd numbers. The above definition of parity applies only to integer numbers, hence it cannot be applied to numbers like 1/2 or 4.201. See the section "Higher mathematics" below for some extensions of the notion of parity to a larger class of "numbers" or in other more general settings. Even and odd numbers have opposite parities, e.g., 22 (even number) and 13 (odd number) have opposite parities. In particular, the parity of zero is even. Any two consecutive integers have opposite parity. A number (i.e., integer) expressed in the decimal numeral system is even or odd according to whether its last digit is even or odd. That is, if the last digit is 1, 3, 5, 7, or 9, then it is odd; other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continued Fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction (or terminated continued fraction), the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers a_i are called the coefficients or terms of the continued fraction. It is generally assumed that the numerator of all of the fractions is 1. If arbitrary values and/or functions are used in place of one or more of the numerators or the integers in the denominators, the resulting expression is a generalized continued fraction. When it is ne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Representation
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero) and "1" (one). The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, Juan Caramuel y Lobkowitz, and Gottfried Leibniz. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. Leibniz was specifical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Run-length Encoding
Run-length encoding (RLE) is a form of lossless data compression in which ''runs'' of data (sequences in which the same data value occurs in many consecutive data elements) are stored as a single data value and count, rather than as the original run. This is most efficient on data that contains many such runs, for example, simple graphic images such as icons, line drawings, Conway's Game of Life, and animations. For files that do not have many runs, RLE could increase the file size. RLE may also be used to refer to an early graphics file format supported by CompuServe for compressing black and white images, but was widely supplanted by their later Graphics Interchange Format (GIF). RLE also refers to a little-used image format in Windows 3.x, with the extension rle, which is a run-length encoded bitmap, used to compress the Windows 3.x startup screen. Example Consider a screen containing plain black text on a solid white background. There will be many long runs of white pixe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floor And Ceiling Functions
In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least integer greater than or equal to , denoted or . For example, , , , and . Historically, the floor of has been–and still is–called the integral part or integer part of , often denoted (as well as a variety of other notations). Some authors may define the integral part as if is nonnegative, and otherwise: for example, and . The operation of truncation generalizes this to a specified number of digits: truncation to zero significant digits is the same as the integer part. For an integer, . Notation The ''integral part'' or ''integer part'' of a number ( in the original) was first defined in 1798 by Adrien-Marie Legendre in his proof of the Legendre's formula. Carl Friedrich Gauss introduced the square bracket notation in h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Programming
In computer science, functional programming is a programming paradigm where programs are constructed by applying and composing functions. It is a declarative programming paradigm in which function definitions are trees of expressions that map values to other values, rather than a sequence of imperative statements which update the running state of the program. In functional programming, functions are treated as first-class citizens, meaning that they can be bound to names (including local identifiers), passed as arguments, and returned from other functions, just as any other data type can. This allows programs to be written in a declarative and composable style, where small functions are combined in a modular manner. Functional programming is sometimes treated as synonymous with purely functional programming, a subset of functional programming which treats all functions as deterministic mathematical functions, or pure functions. When a pure function is call ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |