|
Bifurcation Theory
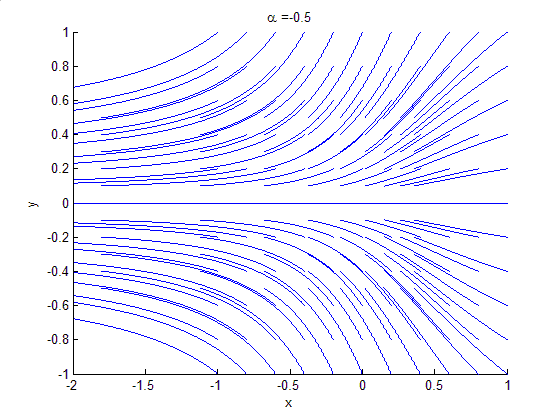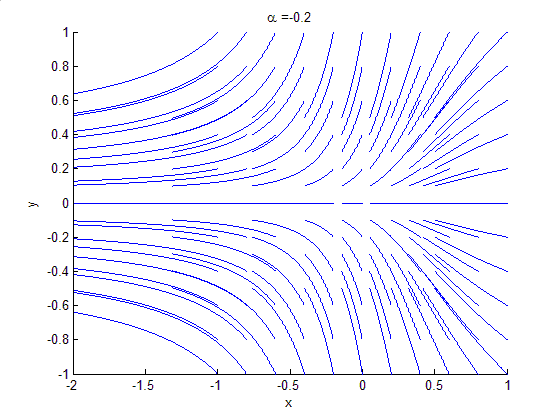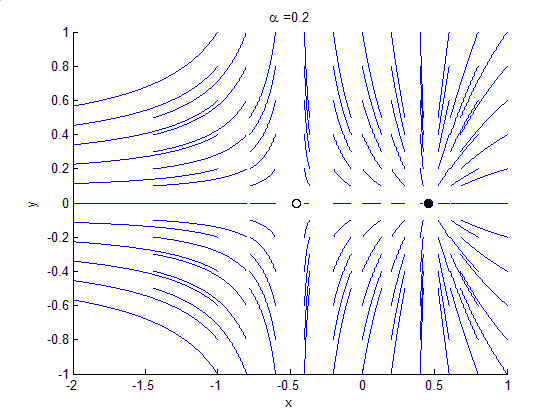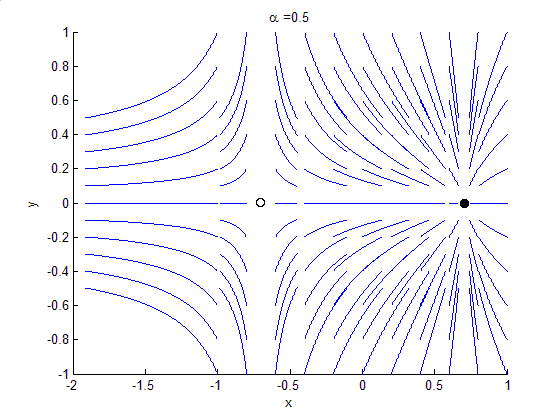
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematics, mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by Ordinary differential equation, ordinary, Delay differential equation, delay or Partial differential equation, partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Matrix And Determinant
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of components of function values, then its determinant is called the Jacobian determinant. Both the matrix and (if applicable) the determinant are often referred to simply as the Jacobian. They are named after Carl Gustav Jacob Jacobi. The Jacobian matrix is the natural generalization to vector valued functions of several variables of the derivative and the differential of a usual function. This generalization includes generalizations of the inverse function theorem and the implicit function theorem, where the non-nullity of the derivative is replaced by the non-nullity of the Jacobian determinant, and the multiplicative inverse of the derivative is replaced by the inverse of the Jacobian matrix. The Jacobian determinant is fundamentally use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heteroclinic Cycle
In mathematics, a heteroclinic cycle is an invariant set in the phase space of a dynamical system. It is a topological circle of equilibrium points and connecting heteroclinic orbits. If a heteroclinic cycle is asymptotically stable, approaching trajectories spend longer and longer periods of time in a neighbourhood of successive equilibria. In generic dynamical systems heteroclinic connections are of high co-dimension, that is, they will not persist if parameters are varied. Robust heteroclinic cycles A robust heteroclinic cycle is one which persists under small changes in the underlying dynamical system. Robust cycles often arise in the presence of symmetry or other constraints which force the existence of invariant hyperplanes. A prototypical example of a robust heteroclinic cycle is the Guckenheimer–Holmes cycle. This cycle has also been studied in the context of rotating convection, and as three competing species in population dynamics Population dynamics is the t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addison-Wesley
Addison–Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson plc, a global publishing and education company. In addition to publishing books, Addison–Wesley also distributes its technical titles through the O'Reilly Online Learning e-reference service. Addison–Wesley's majority of sales derive from the United States (55%) and Europe (22%). The Addison–Wesley Professional Imprint produces content including books, eBooks, and video for the professional IT worker including developers, programmers, managers, system administrators. Classic titles include '' The Art of Computer Programming'', '' The C++ Programming Language'', '' The Mythical Man-Month'', and '' Design Patterns''. History Lew Addison Cummings and Melbourne Wesley Cummings founded Addison–Wesley in 1942, with the first book published by Addison–Wesley being Massachusetts Institute of Technology professor Francis Weston Sears' ''Mechanics''. Its first comput ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saddle Point
In mathematics, a saddle point or minimax point is a Point (geometry), point on the surface (mathematics), surface of the graph of a function where the slopes (derivatives) in orthogonal directions are all zero (a Critical point (mathematics), critical point), but which is not a local extremum of the function. An example of a saddle point is when there is a critical point with a relative minimum along one axial direction (between peaks) and a relative maxima and minima, maximum along the crossing axis. However, a saddle point need not be in this form. For example, the function f(x,y) = x^2 + y^3 has a critical point at (0, 0) that is a saddle point since it is neither a relative maximum nor relative minimum, but it does not have a relative maximum or relative minimum in the y-direction. The name derives from the fact that the prototypical example in two dimensions is a surface (mathematics), surface that ''curves up'' in one direction, and ''curves down'' in a different dir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Cycle
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912). Definition We consider a two-dimensional dynamical system of the form x'(t)=V(x(t)) where V : \R^2 \to \R^2 is a smooth function. A ''trajectory'' of this system is some smooth function x(t) with values in \mathbb^2 which satisfies this differential equation. Such a trajectory is called ''closed'' (or ''periodic'') if it is not constant but returns to its starting point, i.e. if there exists some t_0>0 such that x(t + t_0) = x(t) for all t \in \R. An orbit (dynamics), orbit is the ima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |