2006 Operas

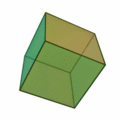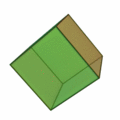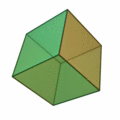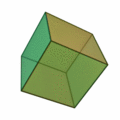
picture info	2006 Operas 6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. In mathematics A six-sided polygon is a hexagon, one of the three regular polygons capable of tiling the plane. A hexagon also has 6 edges as well as 6 internal and external angles. 6 is the second smallest composite number. It is also the first number that is the sum of its proper divisors, making it the smallest perfect number. It is also the only perfect number that doesn't have a digital root of 1. 6 is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist. 6 is the largest of the four all-Harshad numbers. 6 is the 2nd superior highly composite number, the 2nd colossally abundant number, the 3rd triangular number, the 4th highly composite number, a pronic number, a congruent number, a harmonic divisor number, and a semiprime. 6 is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Senary A senary () numeral system (also known as base-6, heximal, or seximal) has 6, six as its radix, base. It has been adopted independently by a small number of cultures. Like the decimal base 10, the base is a semiprime, though it is unique as the product of the only two consecutive numbers that are both prime (2 and 3). As six is a superior highly composite number, many of the arguments made in favor of the duodecimal system also apply to the senary system. Formal definition The standard Set (mathematics), set of digits in the senary system is \mathcal_6 = \lbrace 0, 1, 2, 3, 4, 5\rbrace, with the linear order 0 < 1 < 2 < 3 < 4 < 5. Let $\mathcal_6^$ be the Kleene closure of $\mathcal_6$ , where $ab$ is the operation of string concatenation for $a, b \in \mathcal^$ . The senary number system for natural numbers $\mathcal_6$ is the quotient set $\mathcal_6^* / \sim$ equipped with a shortlex order, where the equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Hebrew (language) Hebrew (; ''ʿÎbrit'') is a Northwest Semitic languages, Northwest Semitic language within the Afroasiatic languages, Afroasiatic language family. A regional dialect of the Canaanite languages, it was natively spoken by the Israelites and remained in regular use as a first language until after 200 CE and as the Sacred language, liturgical language of Judaism (since the Second Temple period) and Samaritanism. The language was Revival of the Hebrew language, revived as a spoken language in the 19th century, and is the only successful large-scale example of Language revitalization, linguistic revival. It is the only Canaanite language, as well as one of only two Northwest Semitic languages, with the other being Aramaic, still spoken today. The earliest examples of written Paleo-Hebrew alphabet, Paleo-Hebrew date back to the 10th century BCE. Nearly all of the Hebrew Bible is written in Biblical Hebrew, with much of its present form in the dialect that scholars believe flourish ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Perfect Number In number theory, a perfect number is a positive integer that is equal to the sum of its positive proper divisors, that is, divisors excluding the number itself. For instance, 6 has proper divisors 1, 2 and 3, and 1 + 2 + 3 = 6, so 6 is a perfect number. The next perfect number is 28, since 1 + 2 + 4 + 7 + 14 = 28. The first four perfect numbers are 6 (number), 6, 28 (number), 28, 496 (number), 496 and 8128 (number), 8128. The sum of proper divisors of a number is called its aliquot sum, so a perfect number is one that is equal to its aliquot sum. Equivalently, a perfect number is a number that is half the sum of all of its positive divisors; in symbols, \sigma_1(n)=2n where \sigma_1 is the sum-of-divisors function. This definition is ancient, appearing as early as Euclid's Elements, Euclid's ''Elements'' (VII.22) where it is called (''perfect'', ''ideal'', or ''complete number''). Euclid also proved a formation rule (IX.36) whereby \frac is an even perfect number whenever q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Composite Number A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Accordingly it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime number, prime, or the Unit (ring theory), unit 1, so the composite numbers are exactly the numbers that are not prime and not a unit. E.g., the integer 14 is a composite number because it is the product of the two smaller integers 2 × 7 but the integers 2 and 3 are not because each can only be divided by one and itself. The composite numbers up to 150 are: :4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Natural Number In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive integers Some authors acknowledge both definitions whenever convenient. Sometimes, the whole numbers are the natural numbers as well as zero. In other cases, the ''whole numbers'' refer to all of the integers, including negative integers. The counting numbers are another term for the natural numbers, particularly in primary education, and are ambiguous as well although typically start at 1. The natural numbers are used for counting things, like "there are ''six'' coins on the table", in which case they are called ''cardinal numbers''. They are also used to put things in order, like "this is the ''third'' largest city in the country", which are called ''ordinal numbers''. Natural numbers are also used as labels, like Number (sports), jersey ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Morse Code Morse code is a telecommunications method which Character encoding, encodes Written language, text characters as standardized sequences of two different signal durations, called ''dots'' and ''dashes'', or ''dits'' and ''dahs''. Morse code is named after Samuel Morse, one of the early developers of the system adopted for electrical telegraphy. International Morse code encodes the 26 ISO basic Latin alphabet, basic Latin letters to , one Diacritic, accented Latin letter (), the Arabic numerals, and a small set of punctuation and procedural signals (Prosigns for Morse code, prosigns). There is no distinction between upper and lower case letters. Each Morse code symbol is formed by a sequence of ''dits'' and ''dahs''. The ''dit'' duration can vary for signal clarity and operator skill, but for any one message, once the rhythm is established, a beat (music), half-beat is the basic unit of time measurement in Morse code. The duration of a ''dah'' is three times the duration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Egyptian Numerals The system of ancient Egyptian numerals was used in Ancient Egypt from around 3000 BC until the early first millennium AD. It was a system of numeration based on multiples of ten, often rounded off to the higher power, written in hieroglyphs. The Egyptians had no concept of a positional notation such as the decimal system."The Story of Numbers" by John McLeish The hieratic form of numerals stressed an exact finite series notation, ciphered one-to-one onto the Egyptian alphabet. Digits and numbers The following hieroglyphs were used to denote powers of ten: Multiples of these values were expressed by repeating the symbol as many times as needed. For instance, a stone carving from Karnak shows the number 4,622 as: Egyptian hieroglyphs could be written in both directions (and even vertically). In this example the symbols decrease in value from top to bottom and from left to right. On the original stone carving, it is right-to-left, and the signs are thus reversed. Zero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Babylonian Cuneiform Numerals Babylonian cuneiform numerals, also used in Assyria and Chaldea, were written in cuneiform, using a wedge-tipped reed stylus to print a mark on a soft clay tablet which would be exposed in the sun to harden to create a permanent record. The Babylonians, who were famous for their astronomical observations, as well as their calculations (aided by their invention of the abacus), used a sexagesimal (base-60) positional numeral system inherited from either the Sumerian or the Akkadian civilizations. Neither of the predecessors was a positional system (having a convention for which 'end' of the numeral represented the units). Origin This system first appeared around 2000 BC; its structure reflects the decimal lexical numerals of Semitic languages rather than Sumerian lexical numbers. However, the use of a special Sumerian sign for 60 (beside two Semitic signs for the same number) attests to a relation with the Sumerian system. Symbols The Babylonian system is credited as b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Armenian Numerals Armenian numerals form a historic numeral system created using the majuscules (uppercase letters) of the Armenian alphabet. There was no notation for zero in the old system, and the numeric values for individual letters were added together. The principles behind this system are the same as for the ancient Greek numerals and Hebrew numerals. In modern Armenia, the familiar Arabic numerals are used. In contemporary writing, Armenian numerals are used more or less like Roman numerals in modern English, e.g. Գարեգին Բ. means Garegin II and Գ. գլուխ means ''Chapter III'' (as a headline). The final two letters of the Armenian alphabet, "o" (Օ) and "fe" (Ֆ), were added to the Armenian alphabet only after Arabic numerals were already in use, to facilitate transliteration of other languages. Thus, they sometimes have a numerical value assigned to them. Notation As in Hebrew and ancient notation, in Armenian numerals distinct symbols represent multiples of po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Malayalam Numerals Malayalam numerals are the numeral system of the Malayalam script used by Malayalam in Kerala Kerala ( , ) is a States and union territories of India, state on the Malabar Coast of India. It was formed on 1 November 1956, following the passage of the States Reorganisation Act, by combining Malayalam-speaking regions of the erstwhile .... It is one of several Indian numeral systems. This system is archaic and nowadays the Hindu–Arabic numeral system is used commonly. However it is still found in many documents of cultural or historical importance. Base numbers Below is a list of Malayalam numerals with their Hindu–Arabic equivalents as well as their respective Malayalam translations and transliterations. Originally, a number like "11" would have been written as "൰൧" and not "൧൧" to match the Malayalam word for 11 and "10,00,000" as "൰൱൲" similar to the Tamil numeral system. Later on this system got reformed to be more similar to the Hindu–Arabic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Saraiki Language Saraiki ( ', ; also spelt Siraiki, or Seraiki) is an Indo-Aryan language of the Lahnda group. "The existence of Lahnda as a separate language has long been recognised under various names such as Jatki, Multani, Hindki or Hindko and Western Panjabi....it is called Multani, but this name properly applies only to the form of Lahnda spoken around Multan and the neighbourhood." It is spoken by 28.84 million people, as per the 2023 Pakistani census, taking prevalence in Southern Punjab with remants in Northern Sindh and the Derajat region. Saraiki has partial mutual intelligibility with Standard Punjabi, and it shares with it a large portion of its vocabulary and Linguistic morphology, morphology. At the same time in #Phonology, its phonology it is radically different (particularly in the lack of tones, the preservation of the voiced aspirates and the development of implosive consonants), and has important grammatical features in common with the Sindhi language spoken to the south. S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Tamil Numerals The Tamil language has Numeral (linguistics), number words and dedicated symbols for them in the Tamil script. Basic numbering in Tamil Zero Old Tamil possesses a special numerical character for zero ''(see #Old Tamil numerals, Old Tamil numerals below),'' which is read as (literally, no/nothing). Modern Tamil words for zero include () or (). First ten numbers () Transcribing other numbers Reproductive and attributive prefixes Tamil has a numeric prefix for each number from 1 to 9, which can be added to the words for the powers of ten (ten, hundred, thousand, etc.) to form multiples of them. For instance, the word for fifty, () is a combination of (, the prefix for five) and (, which is ten). The prefix for nine changes with respect to the succeeding base 10. + the unvoiced consonant of the succeeding base 10 forms the prefix for nine. For instance, 90 is + ( being the unvoiced version of ), hence, ). These are typically void in the Tamil language except f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]