|
Buoyancy
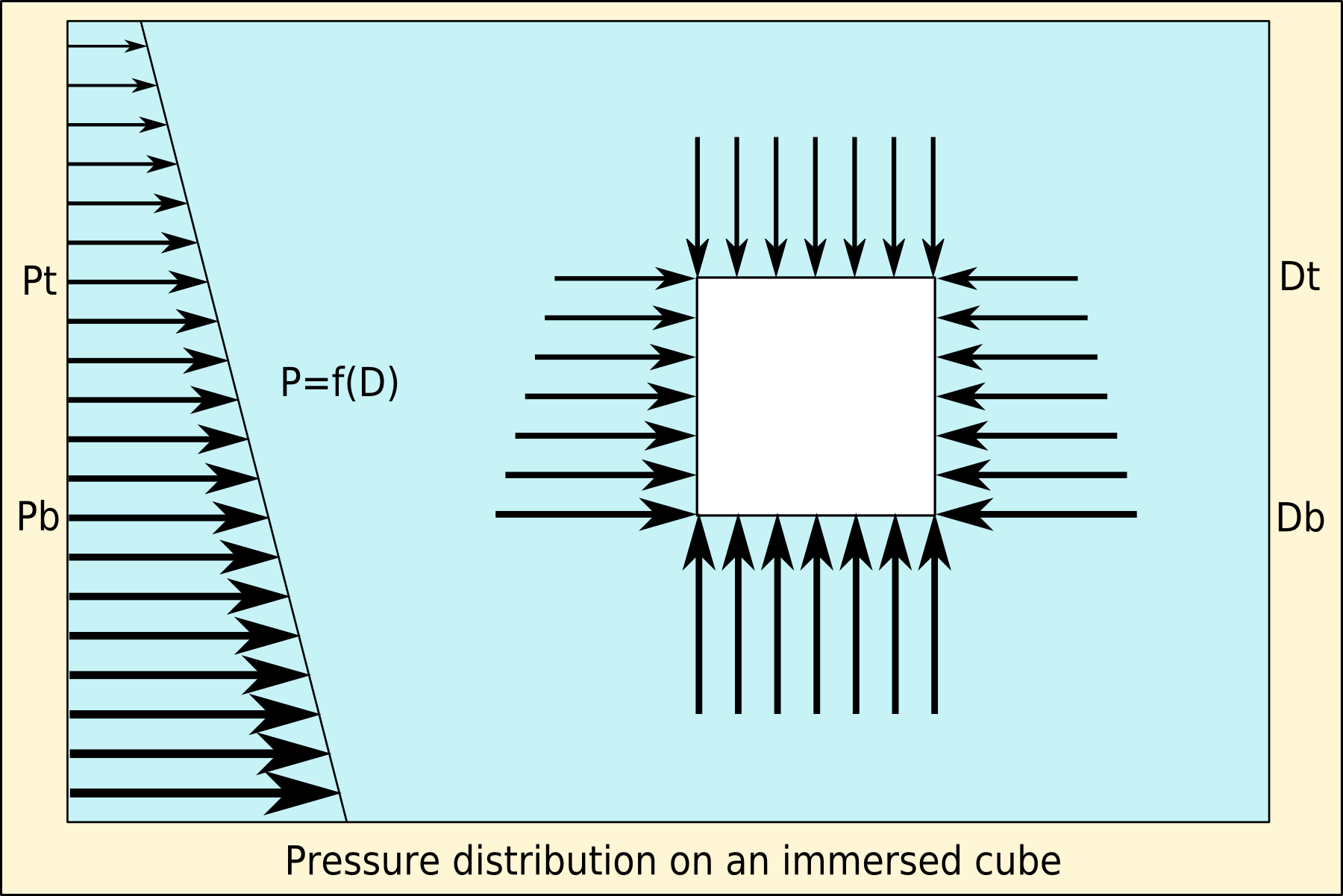
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus, the pressure at the bottom of a column of fluid is greater than at the top of the column. Similarly, the pressure at the bottom of an object submerged in a fluid is greater than at the top of the object. The pressure difference results in a net upward force on the object. The magnitude of the force is proportional to the pressure difference, and (as explained by Archimedes' principle) is equivalent to the weight of the fluid that would otherwise occupy the submerged volume of the object, i.e. the Displacement (fluid), displaced fluid. For this reason, an object with average density greater than the surrounding fluid tends to sink because its weight is greater than the weight of the fluid it displaces. If the objec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes' Principle
Archimedes' principle states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimedes' principle is a law of physics fundamental to fluid mechanics. It was formulated by Archimedes of Syracuse. Explanation In '' On Floating Bodies'', Archimedes suggested that (c. 246 BC): Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising or sinking. In simple words, Archim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be used: \rho = \frac, where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate this quantity is more specifically called specific weight. For a pure substance, the density is equal to its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium is the densest known element at standard conditions for temperature and pressure. To simplify comparisons of density across different systems of units, it is sometimes replaced by the dimensionless quantity "relative den ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Center Of Gravity
In physics, the center of mass of a distribution of mass in space (sometimes referred to as the barycenter or balance point) is the unique point at any given time where the weighted relative position of the distributed mass sums to zero. For a rigid body containing its center of mass, this is the point to which a force may be applied to cause a linear acceleration without an angular acceleration. Calculations in mechanics are often simplified when formulated with respect to the center of mass. It is a hypothetical point where the entire mass of an object may be assumed to be concentrated to visualise its motion. In other words, the center of mass is the particle equivalent of a given object for application of Newton's laws of motion. In the case of a single rigid body, the center of mass is fixed in relation to the body, and if the body has uniform density, it will be located at the centroid. The center of mass may be located outside the physical body, as is sometimes the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection
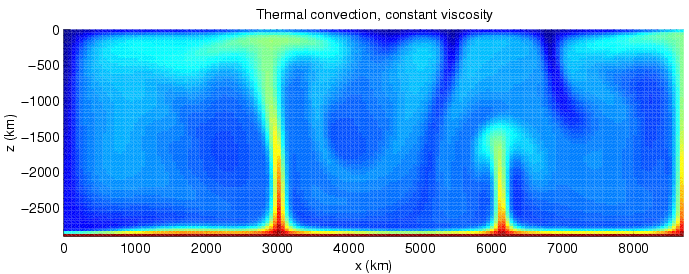
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenistic Sicily, Sicily. Although few details of his life are known, based on his surviving work, he is considered one of the leading scientists in classical antiquity, and one of the greatest mathematicians of all time. Archimedes anticipated modern calculus and mathematical analysis, analysis by applying the concept of the Cavalieri's principle, infinitesimals and the method of exhaustion to derive and rigorously prove many geometry, geometrical theorem, theorems, including the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral. Archimedes' other math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volume Integral
In mathematics (particularly multivariable calculus), a volume integral (∭) is an integral over a 3-dimensional domain; that is, it is a special case of multiple integrals. Volume integrals are especially important in physics for many applications, for example, to calculate flux densities, or to calculate mass from a corresponding density function. In coordinates Often the volume integral is represented in terms of a differential volume element dV=dx\, dy\, dz . \iiint_D f(x,y,z)\,dV. It can also mean a triple integral within a region D \subset \R^3 of a function f(x,y,z), and is usually written as: \iiint_D f(x,y,z)\,dx\,dy\,dz. A volume integral in cylindrical coordinates is \iiint_D f(\rho,\varphi,z) \rho \,d\rho \,d\varphi \,dz, and a volume integral in spherical coordinates (using the ISO convention for angles with \varphi as the azimuth and \theta measured from the polar axis (see more on conventions)) has the form \iiint_D f(r,\theta,\varphi) r^2 \sin\theta \,dr \, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, one may integrate over this surface a scalar field (that is, a function of position which returns a scalar as a value), or a vector field (that is, a function which returns a vector as value). If a region R is not flat, then it is called a ''surface'' as shown in the illustration. Surface integrals have applications in physics, particularly in the classical theories of electromagnetism and fluid mechanics. Surface integrals of scalar fields Assume that ''f'' is a scalar, vector, or tensor field defined on a surface ''S''. To find an explicit formula for the surface integral of ''f'' over ''S'', we need to parameterize ''S'' by defining a system of curvilinear coordinates on ''S'', like the latitude and longitude on a sphere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kronecker Delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise: \delta_ = \begin 0 &\text i \neq j, \\ 1 &\text i=j. \end or with use of Iverson brackets: \delta_ = =j, For example, \delta_ = 0 because 1 \ne 2, whereas \delta_ = 1 because 3 = 3. The Kronecker delta appears naturally in many areas of mathematics, physics, engineering and computer science, as a means of compactly expressing its definition above. Generalized versions of the Kronecker delta have found applications in differential geometry and modern tensor calculus, particularly in formulations of gauge theory and topological field models. In linear algebra, the n\times n identity matrix \mathbf has entries equal to the Kronecker delta: I_ = \delta_ where i and j take the values 1,2,\cdots,n, and the inner product of vectors can be written as \mathbf\cdot\mathbf = \sum_^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the deformed state, placement, or configuration. The second order tensor consists of nine components \sigma_ and relates a unit-length direction vector e to the ''traction vector'' T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sum_\sigma_e_i. The SI base units of both stress tensor and traction vector are newton per square metre (N/m2) or pascal (Pa), corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of mater ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canard Colvert 02
Canard (meaning "duck" in French) may refer to: Aviation *Canard (aeronautics), a small wing in front of an aircraft's main wing * Aviafiber Canard 2FL, a single seat recreational aircraft of canard design * Voisin Canard, aircraft developed by the Voisin brothers People * Marius Canard (1888–1982), French Orientalist and historian * Nicolas-François Canard (c. 1750 – 1833), French mathematician and economist Places in Canada * Canard, Nova Scotia, a group of hamlets and villages *Canard River, a river in Nova Scotia Other uses * Canard Pars, fictional character from the Japanese science fiction manga series ''Mobile Suit Gundam SEED Astray'' *'' Canard PC'', a French magazine devoted to computer gaming * Canard, an alternative name for a diving plane, small wings attached to the front of a submarine or an automobile See also *Antisemitic canard Antisemitic tropes, also known as antisemitic canards or antisemitic libels, are " sensational reports, misrepres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dasymeter
A dasymeter was meant initially as a device to demonstrate the buoyant effect of gases like air (as shown in the adjacent pictures). A dasymeter which allows weighing acts as a densimeter used to measure the density of gases. Principle The Principle of Archimedes permits to derive a formula which does not rely on any information of volume: a sample, the big sphere in the adjacent images, of known mass-density is weighed in vacuum and then immersed into the gas and weighed again. : \frac = \frac \, (The above formula was taken from the article buoyancy and still has to be solved for the density of the gas.) From the known mass density of the sample (sphere) and its two weight-values, the mass-density of the gas can be calculated as: : = \frac \times Construction and use It consists of a thin sphere made of glass, ideally with an average density close to that of the gas to be investigated. This sphere is immersed in the gas and weighed. History of the dasymeter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |