|
Beta-binomial Distribution
In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of ''n'' trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data. The beta-binomial is a one-dimensional version of the Dirichlet-multinomial distribution as the binomial and beta distributions are univariate versions of the multinomial and Dirichlet distributions respectively. The special case where ''α'' and ''β'' are integers is also known as the negative hypergeometric distribution. Motivation and derivation As a compound ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta-binomial Distribution Pmf
In probability theory and statistics, the beta-binomial distribution is a family of discrete probability distributions on a finite support of non-negative integers arising when the probability of success in each of a fixed or known number of Bernoulli trials is either unknown or random. The beta-binomial distribution is the binomial distribution in which the probability of success at each of ''n'' trials is not fixed but randomly drawn from a beta distribution. It is frequently used in Bayesian statistics, empirical Bayes methods and classical statistics to capture overdispersion in binomial type distributed data. The beta-binomial is a one-dimensional version of the Dirichlet-multinomial distribution as the binomial and beta distributions are univariate versions of the multinomial and Dirichlet distributions respectively. The special case where ''α'' and ''β'' are integers is also known as the negative hypergeometric distribution. Motivation and derivation As a compound di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overdispersion
In statistics, overdispersion is the presence of greater variability (statistical dispersion) in a data set than would be expected based on a given statistical model. A common task in applied statistics is choosing a parametric model to fit a given set of empirical observations. This necessitates an assessment of the fit of the chosen model. It is usually possible to choose the model parameters in such a way that the theoretical population mean of the model is approximately equal to the sample mean. However, especially for simple models with few parameters, theoretical predictions may not match empirical observations for higher moments. When the observed variance is higher than the variance of a theoretical model, overdispersion has occurred. Conversely, underdispersion means that there was less variation in the data than predicted. Overdispersion is a very common feature in applied data analysis because in practice, populations are frequently heterogeneous (non-uniform) contrary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
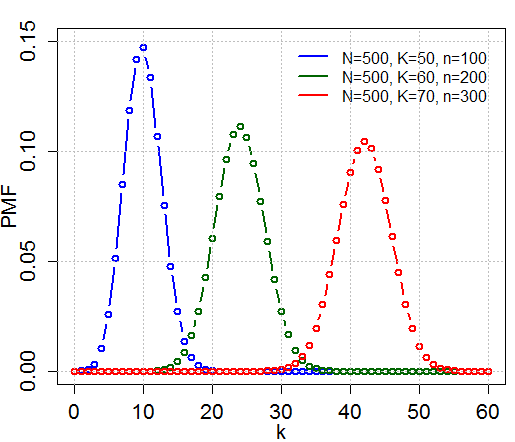
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a Probability distribution#Discrete probability distribution, discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite Statistical population, population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of Binary variable, two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pólya Urn Model
In statistics, a Pólya urn model (also known as a Pólya urn scheme or simply as Pólya's urn), named after George Pólya, is a family of urn models that can be used to interpret many commonly used statistical models. The model represents objects of interest (such as atoms, people, cars, etc.) as colored balls in an urn. In the basic Pólya urn model, the experimenter puts ''x'' white and ''y'' black balls into an urn. At each step, one ball is drawn uniformly at random from the urn, and its color observed; it is then returned in the urn, and an additional ball of the same color is added to the urn. If by random chance, more black balls are drawn than white balls in the initial few draws, it would make it more likely for more black balls to be drawn later. Similarly for the white balls. Thus the urn has a self-reinforcing property (" the rich get richer"). It is the opposite of sampling without replacement, where every time a particular value is observed, it is less likely to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Urn Model
In probability and statistics, an urn problem is an idealized mental exercise in which some objects of real interest (such as atoms, people, cars, etc.) are represented as colored balls in an urn or other container. One pretends to remove one or more balls from the urn; the goal is to determine the probability of drawing one color or another, or some other properties. A number of important variations are described below. An urn model is either a set of probabilities that describe events within an urn problem, or it is a probability distribution, or a family of such distributions, of random variables associated with urn problems. History In ''Ars Conjectandi'' (1713), Jacob Bernoulli considered the problem of determining, given a number of pebbles drawn from an urn, the proportions of different colored pebbles within the urn. This problem was known as the ''inverse probability'' problem, and was a topic of research in the eighteenth century, attracting the attention of Abraham d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Distribution
In probability and statistics, a compound probability distribution (also known as a mixture distribution or contagious distribution) is the probability distribution that results from assuming that a random variable is distributed according to some parametrized distribution, with (some of) the parameters of that distribution themselves being random variables. If the parameter is a scale parameter, the resulting mixture is also called a scale mixture. The compound distribution ("unconditional distribution") is the result of marginalizing (integrating) over the ''latent'' random variable(s) representing the parameter(s) of the parametrized distribution ("conditional distribution"). Definition A compound probability distribution is the probability distribution that results from assuming that a random variable X is distributed according to some parametrized distribution F with an unknown parameter \theta that is again distributed according to some other distribution G. The resulting d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjugate Prior
In Bayesian probability theory, if, given a likelihood function p(x \mid \theta), the posterior distribution p(\theta \mid x) is in the same probability distribution family as the prior probability distribution p(\theta), the prior and posterior are then called conjugate distributions with respect to that likelihood function and the prior is called a conjugate prior for the likelihood function p(x \mid \theta). A conjugate prior is an algebraic convenience, giving a closed-form expression for the posterior; otherwise, numerical integration may be necessary. Further, conjugate priors may clarify how a likelihood function updates a prior distribution. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory.Howard Raiffa and Robert Schlaifer. ''Applied Statistical Decision Theory''. Division of Research, Graduate School of Business Administration, Harvard University, 1961. A similar c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Distribution
In probability theory and statistics, the beta distribution is a family of continuous probability distributions defined on the interval [0, 1] or (0, 1) in terms of two positive Statistical parameter, parameters, denoted by ''alpha'' (''α'') and ''beta'' (''β''), that appear as exponents of the variable and its complement to 1, respectively, and control the shape parameter, shape of the distribution. The beta distribution has been applied to model the behavior of random variables limited to intervals of finite length in a wide variety of disciplines. The beta distribution is a suitable model for the random behavior of percentages and proportions. In Bayesian inference, the beta distribution is the conjugate prior distribution, conjugate prior probability distribution for the Bernoulli distribution, Bernoulli, binomial distribution, binomial, negative binomial distribution, negative binomial, and geometric distribution, geometric distributions. The formulation of the beta dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
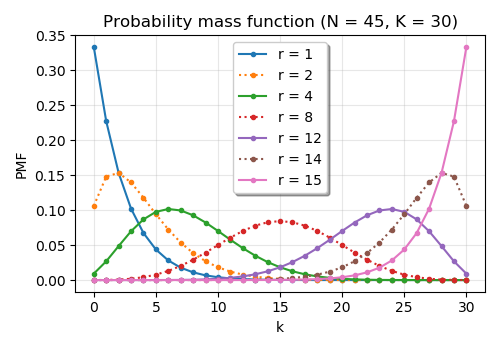
Negative Hypergeometric Distribution
In probability theory and statistics, the negative hypergeometric distribution describes probabilities for when sampling from a finite population without replacement in which each sample can be classified into two mutually exclusive categories like Pass/Fail or Employed/Unemployed. As random selections are made from the population, each subsequent draw decreases the population causing the probability of success to change with each draw. Unlike the standard hypergeometric distribution, which describes the number of successes in a fixed sample size, in the negative hypergeometric distribution, samples are drawn until r failures have been found, and the distribution describes the probability of finding k successes in such a sample. In other words, the negative hypergeometric distribution describes the likelihood of k successes in a sample with exactly r failures. Definition There are N elements, of which K are defined as "successes" and the rest are "failures". Elements are drawn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Distribution
In probability and statistics, the Dirichlet distribution (after Peter Gustav Lejeune Dirichlet), often denoted \operatorname(\boldsymbol\alpha), is a family of continuous multivariate probability distributions parameterized by a vector of positive reals. It is a multivariate generalization of the beta distribution, (Chapter 49: Dirichlet and Inverted Dirichlet Distributions) hence its alternative name of multivariate beta distribution (MBD). Dirichlet distributions are commonly used as prior distributions in Bayesian statistics, and in fact, the Dirichlet distribution is the conjugate prior of the categorical distribution and multinomial distribution. The infinite-dimensional generalization of the Dirichlet distribution is the '' Dirichlet process''. Definitions Probability density function The Dirichlet distribution of order with parameters has a probability density function with respect to Lebesgue measure on the Euclidean space given by f \left(x_1,\ldots, x_; \alp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |