|
Bessel Functions
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, which represents the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. #Spherical Bessel functions, Spherical Bessel functions with half-integer \alpha are obtained when solving the Helmholtz equation in spherical coordinates. Applications Bessel's equation arise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kaiser Window
The Kaiser window, also known as the Kaiser–Bessel window, was developed by James Kaiser at Bell Laboratories. It is a one-parameter family of window functions used in finite impulse response filter design and spectral estimation, spectral analysis. The Kaiser window approximates the DPSS window which Spectral concentration problem, maximizes the energy concentration in the main lobe but which is difficult to compute. Definition The Kaiser window and its Fourier transform are given by: : w_0(x) \triangleq \left\ \quad \stackrel\quad \frac , where: * is the zeroth-order Modified_Bessel_function#Modified_Bessel_functions:_Iα,_Kα, modified Bessel function of the first kind, * is the window duration, and * is a non-negative real number that determines the shape of the window. In the frequency domain, it determines the trade-off between main-lobe width and side lobe level, which is a central decision in window design. * Sometimes the Kaiser window is parametrized b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Conduction (heat)
Thermal conduction is the diffusion of thermal energy (heat) within one material or between materials in contact. The higher temperature object has molecules with more kinetic energy; collisions between molecules distributes this kinetic energy until an object has the same kinetic energy throughout. Thermal conductivity, frequently represented by , is a property that relates the rate of heat loss per unit area of a material to its rate of change of temperature. Essentially, it is a value that accounts for any property of the material that could change the way it conducts heat. Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becomi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Frequency Modulation Synthesis
Frequency modulation synthesis (or FM synthesis) is a form of Synthesizer#Sound synthesis, sound synthesis whereby the frequency of a waveform is changed by Frequency modulation, modulating its frequency with a modulator. The instantaneous frequency, (instantaneous) frequency of an oscillator is altered in accordance with the amplitude of a modulating signal. FM synthesis can create both harmonic and Inharmonicity, inharmonic sounds. To synthesize harmonic sounds, the modulating signal must have a harmonic relationship to the original carrier signal. As the amount of frequency modulation increases, the sound grows progressively complex. Through the use of modulators with frequencies that are non-integer multiples of the carrier signal (i.e. inharmonic), inharmonic bell-like and percussive spectra can be created. FM synthesis using analog oscillators may result in pitch instability. However, FM synthesis can also be implemented digitally, which is more stable and became standard pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
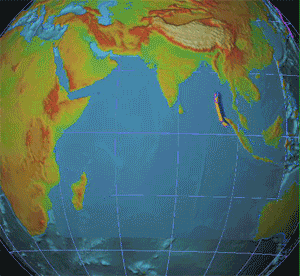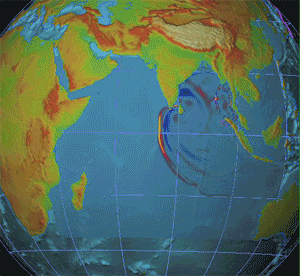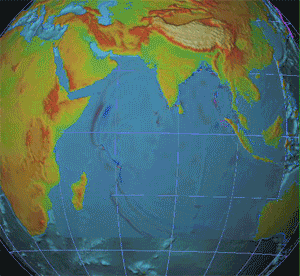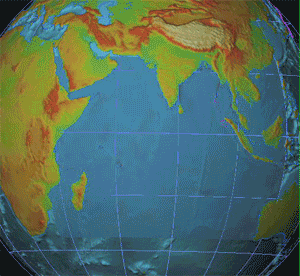
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geophysics
Geophysics () is a subject of natural science concerned with the physical processes and Physical property, properties of Earth and its surrounding space environment, and the use of quantitative methods for their analysis. Geophysicists conduct investigations across a wide range of scientific disciplines. The term ''geophysics'' classically refers to solid earth applications: Earth's figure of the Earth, shape; its gravitational, Earth's magnetic field, magnetic fields, and electromagnetic fields; its structure of the Earth, internal structure and Earth#Chemical composition, composition; its geodynamics, dynamics and their surface expression in plate tectonics, the generation of magmas, volcanism and rock formation. However, modern geophysics organizations and pure scientists use a broader definition that includes the water cycle including snow and ice; geophysical fluid dynamics, fluid dynamics of the oceans and the atmosphere; atmospheric electricity, electricity and magnetism in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Density Function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be equal to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. More precisely, the PDF is used to specify the probability of the random variable falling ''within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Angular Resolution
Angular resolution describes the ability of any image-forming device such as an Optical telescope, optical or radio telescope, a microscope, a camera, or an Human eye, eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. It is used in optics applied to light waves, in antenna (radio), antenna theory applied to radio waves, and in acoustics applied to sound waves. The colloquial use of the term "resolution" sometimes causes confusion; when an optical system is said to have a high resolution or high angular resolution, it means that the perceived distance, or actual angular distance, between resolved neighboring objects is small. The value that quantifies this property, ''θ,'' which is given by the Rayleigh criterion, is low for a system with a high resolution. The closely related term spatial resolution refers to the precision of a measurement with respect to space, which is directly connected to angular resolution in imaging ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. The current standard model of particle physics is based on QFT. History Quantum field theory emerged from the work of generations of theoretical physicists spanning much of the 20th century. Its development began in the 1920s with the description of interactions between light and electrons, culminating in the first quantum field theory—quantum electrodynamics. A major theoretical obstacle soon followed with the appearance and persistence of various infinities in perturbative calculations, a problem only resolved in the 1950s with the invention of the renormalization procedure. A second major barrier came with QFT's apparent inabili ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Propagator
In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. Propagators may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called ''(causal) Green's functions'' (called "''causal''" to distinguish it from the elliptic Laplacian Green's function). Non-relativistic propagators In non-relativistic quantum mechanics, the propagator gives the probability amplitude for a particle to travel from one spatial point (x') at one time (t') to another spatial point (x) at a later time (t). The Green's function G for the Schrödinger equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schrödinger Equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after Erwin Schrödinger, an Austrian physicist, who postulated the equation in 1925 and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of the wave function, the quantum-mechanical characterization of an isolated physical system. The equation was postulated by Schrödinger based on a postulate of Louis de Broglie that all matter has an associated matter wave. The equati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mindlin–Reissner Plate Theory
The Reissner–Mindlin theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin. A similar, but not identical, theory in static setting, had been proposed earlier by Eric Reissner in 1945. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Reissner-Mindlin theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of one tenth the planar dimensions while the Kirchhoff–Love theory is applicable to thinner plates. The form of Reissner-Mindlin plate theory that is most commonly used is actually due to Mindlin and is more properly called ''Mindlin plate theory''. The Reissner theory is slightly different. Both theories include in-plane shear strains and both are extensions of Kirchhoff–Love ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kirchhoff–Love Plate Theory
The Kirchhoff–Love theory of plates is a two-dimensional mathematical model that is used to determine the stresses and deformations in thin plates subjected to forces and moments. This theory is an extension of Euler-Bernoulli beam theory and was developed in 1888 by LoveA. E. H. Love, ''On the small free vibrations and deformations of elastic shells'', Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 p. 491–549. using assumptions proposed by Kirchhoff. The theory assumes that a mid-surface plane can be used to represent a three-dimensional plate in two-dimensional form. The following kinematic assumptions that are made in this theory:Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis. * straight lines normal to the mid-surface remain straight after deformation * straight lines normal to the mid-surface remain normal to the mid-surface after deformation * the thickness of the plate does not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |