Benson's Algorithm

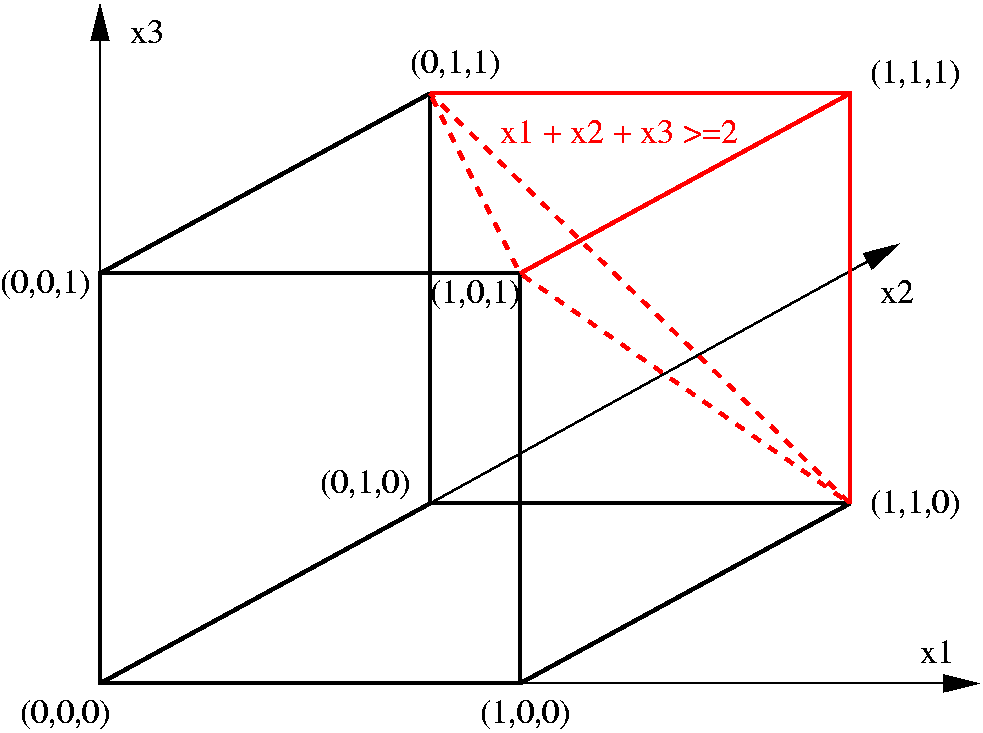
	Benson's Algorithm Benson's algorithm, named after Harold Benson, is a method for solving multi-objective linear programming problems and vector linear programs. This works by finding the "efficient extreme points in the outcome set". The primary concept in Benson's algorithm is to evaluate the upper image of the vector optimization problem by cutting planes. Idea of algorithm Consider a vector linear program :\min_C Px \; \text A x \geq b for P \in \mathbb^, A \in \mathbb^, b \in \mathbb^m and a polyhedral convex ordering cone C having nonempty interior and containing no lines. The feasible set is S=\. In particular, Benson's algorithm finds the extreme points of the set P + C, which is called upper image. In case of C=\mathbb^q_+:=\, one obtains the special case of a multi-objective linear program (multiobjective optimization Multi-objective optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, multiattribute optimization or Pareto opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Benson's Algorithm (Go) In the game Go, Benson's algorithm (named after David B. Benson) can be used to determine the stones which are safe from capture no matter how many turns in a row the opposing player gets, i.e. ''unconditionally alive''. Algorithm Without loss of generality, we describe Benson's algorithm for the Black player. Let ''X'' be the set of all Black chains and ''R'' be the set of all Black-enclosed regions of ''X''. Then Benson's algorithm requires iteratively applying the following two steps until neither is able to remove any more chains or regions: # Remove from ''X'' all Black chains with less than two vital Black-enclosed regions in ''R'', where a Black-enclosed region is ''vital'' to a Black chain in ''X'' if all its empty intersections are also liberties of the chain. # Remove from ''R'' all Black-enclosed regions with a surrounding stone in a chain not in ''X''. The final set X is the set of all unconditionally alive Black chains. Applicability Most strong Computer Go p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Go (game) Go is an abstract strategy board game for two players in which the aim is to surround more territory than the opponent. The game was invented in China more than 2,500 years ago and is believed to be the oldest board game continuously played to the present day. A 2016 survey by the International Go Federation's 75 member nations found that there are over 46 million people worldwide who know how to play Go and over 20 million current players, the majority of whom live in East Asia. The playing pieces are called stones. One player uses the white stones and the other, black. The players take turns placing the stones on the vacant intersections (''points'') of a board. Once placed on the board, stones may not be moved, but stones are removed from the board if the stone (or group of stones) is surrounded by opposing stones on all orthogonally adjacent points, in which case the stone or group is ''captured''. The game proceeds until neither player wishes to make another move. Whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Harold Benson Harold may refer to: People * Harold (given name), including a list of persons and fictional characters with the name * Harold (surname), surname in the English language * András Arató, known in meme culture as "Hide the Pain Harold" Arts and entertainment * ''Harold'' (film), a 2008 comedy film * ''Harold'', an 1876 poem by Alfred, Lord Tennyson * ''Harold, the Last of the Saxons'', an 1848 book by Edward Bulwer-Lytton, 1st Baron Lytton * '' Harold or the Norman Conquest'', an opera by Frederic Cowen * ''Harold'', an 1885 opera by Eduard Nápravník * Harold, a character from the cartoon ''The Grim Adventures of Billy & Mandy'' * Harold & Kumar, a US movie; Harold/Harry is the main actor in the show. Places ;In the United States * Alpine, Los Angeles County, California, an erstwhile settlement that was also known as Harold * Harold, Florida, an unincorporated community * Harold, Kentucky, an unincorporated community * Harold, Missouri, an unincorporated community ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Multi-objective Linear Programming Multi-objective linear programming is a subarea of mathematical optimization. A multiple objective linear program (MOLP) is a linear program with more than one objective function. An MOLP is a special case of a vector linear program. Multi-objective linear programming is also a subarea of Multi-objective optimization. Problem formulation In mathematical terms, a MOLP can be written as: :\min_x Px \quad\text\quad a \leq Bx \leq b,\; \ell \leq x \leq u where B is an (m\times n) matrix, P is a (q\times n) matrix, a is an m-dimensional vector with components in \mathbb \cup \, b is an m-dimensional vector with components in \mathbb \cup \, \ell is an n-dimensional vector with components in \mathbb \cup \, u is an n-dimensional vector with components in \mathbb \cup \ Solution concepts A feasible point x is called ''efficient'' if there is no feasible point y with Px \leq Py, Px \neq Py, where \leq denotes the component-wise ordering. Often in the literature, the aim in multiple ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Vector Optimization Vector optimization is a subarea of mathematical optimization where optimization problems with a vector-valued objective functions are optimized with respect to a given partial ordering and subject to certain constraints. A multi-objective optimization problem is a special case of a vector optimization problem: The objective space is the finite dimensional Euclidean space partially ordered by the component-wise "less than or equal to" ordering. Problem formulation In mathematical terms, a vector optimization problem can be written as: :C\operatorname\min_ f(x) where f: X \to Z for a partially ordered vector space Z. The partial ordering is induced by a cone C \subseteq Z. X is an arbitrary set and S \subseteq X is called the feasible set. Solution concepts There are different minimality notions, among them: * \bar \in S is a ''weakly efficient point'' (weak minimizer) if for every x \in S one has f(x) - f(\bar) \not\in -\operatorname C. * \bar \in S is an ''efficient point' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Cutting-plane Method In mathematical optimization, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory. Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
	Extreme Point In mathematics, an extreme point of a convex set S in a real or complex vector space is a point in S which does not lie in any open line segment joining two points of S. In linear programming problems, an extreme point is also called vertex or corner point of S. Definition Throughout, it is assumed that X is a real or complex vector space. For any p, x, y \in X, say that p x and y if x \neq y and there exists a 0 < t < 1 such that $p = t x + (1-t) y.$ If $K$ is a subset of $X$ and $p \in K,$ then $p$ is called an of $K$ if it does not lie between any two points of $K.$ That is, if there does exist $x, y \in K$ and $0 < t < 1$ such that $x \neq y$ and $p = t x + (1-t) y.$ The set of all extreme points of $K$ is denoted by $\operatorname(K).$ Generalizations If $S$ is a subset of a vector space then a linear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Multiobjective Optimization Multi-objective optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, multiattribute optimization or Pareto optimization) is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives. For a nontrivial multi-objective optimization problem, no single soluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Linear Programming Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the optimization of a linear objective function, subject to linear equality and linear inequality constraints. Its feasible region is a convex polytope, which is a set defined as the intersection of finitely many half spaces, each of which is defined by a linear inequality. Its objective function is a real-valued affine (linear) function defined on this polyhedron. A linear programming algorithm finds a point in the polytope where this function has the smallest (or largest) value if such a point exists. Linear programs are problems that can be expressed in canonical form as : \begin & \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]