|
Bayes Theorem
In probability theory and statistics, Bayes' theorem (alternatively Bayes' law or Bayes' rule), named after Thomas Bayes, describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if the risk of developing health problems is known to increase with age, Bayes' theorem allows the risk to an individual of a known age to be assessed more accurately (by conditioning it on their age) than simply assuming that the individual is typical of the population as a whole. One of the many applications of Bayes' theorem is Bayesian inference, a particular approach to statistical inference. When applied, the probabilities involved in the theorem may have different probability interpretations. With Bayesian probability interpretation, the theorem expresses how a degree of belief, expressed as a probability, should rationally change to account for the availability of related evidence. Bayesian inference is fundamental to Bay ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
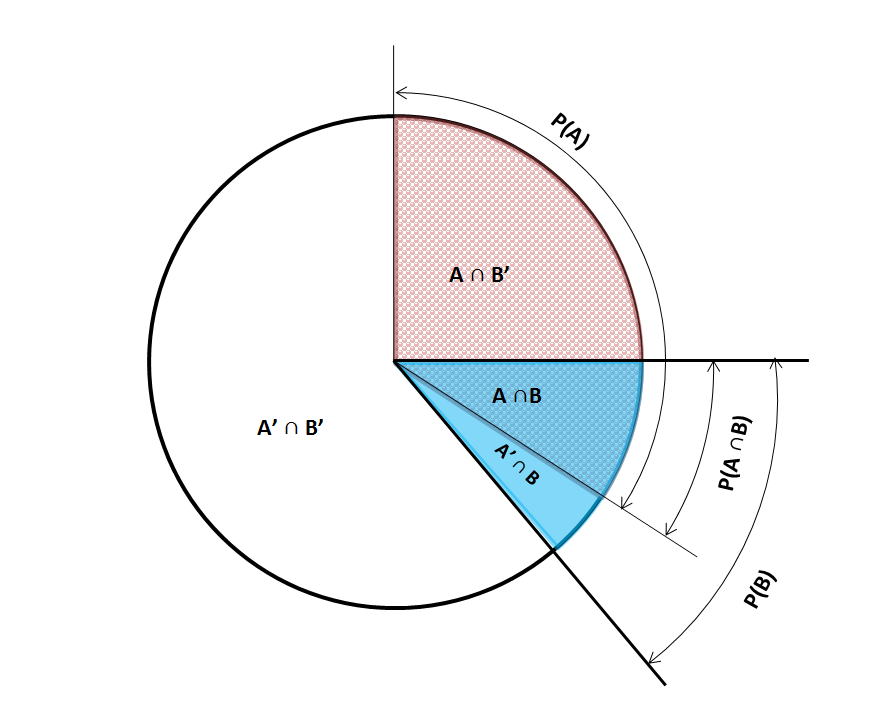
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the Sequential analysis, dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence relation, consequence of two Antecedent (logic), antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred. This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A: P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
True Positive Rate
In medicine and statistics, sensitivity and specificity mathematically describe the accuracy of a test that reports the presence or absence of a medical condition. If individuals who have the condition are considered "positive" and those who do not are considered "negative", then sensitivity is a measure of how well a test can identify true positives and specificity is a measure of how well a test can identify true negatives: * Sensitivity (true positive rate) is the probability of a positive test result, conditioned on the individual truly being positive. * Specificity (true negative rate) is the probability of a negative test result, conditioned on the individual truly being negative. If the true status of the condition cannot be known, sensitivity and specificity can be defined relative to a " gold standard test" which is assumed correct. For all testing, both diagnoses and screening, there is usually a trade-off between sensitivity and specificity, such that higher sensit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two Envelopes Problem
The two envelopes problem, also known as the exchange paradox, is a paradox in probability theory. It is of special interest in decision theory, and for the Bayesian interpretation of probability theory. It is a variant of an older problem known as the necktie paradox. The problem is typically introduced by formulating a hypothetical challenge like the following example: Since the situation is symmetric, it seems obvious that there is no point in switching envelopes. On the other hand, a simple calculation using expected values suggests the opposite conclusion, that it is always beneficial to swap envelopes, since the person stands to gain twice as much money if they switch, while the only risk is halving what they currently have. Introduction Problem Basic setup: A person is given two indistinguishable envelopes, each of which contains a sum of money. One envelope contains twice as much as the other. The person may pick one envelope and keep whatever amount it contains. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boy Or Girl Paradox
The Boy or Girl paradox surrounds a set of questions in probability theory, which are also known as The Two Child Problem, Mr. Smith's Children and the Mrs. Smith Problem. The initial formulation of the question dates back to at least 1959, when Martin Gardner featured it in his October 1959 " Mathematical Games column" in '' Scientific American''. He titled it The Two Children Problem, and phrased the paradox as follows: *Mr. Jones has two children. The older child is a girl. What is the probability that both children are girls? *Mr. Smith has two children. At least one of them is a boy. What is the probability that both children are boys? Gardner initially gave the answers and , respectively, but later acknowledged that the second question was ambiguous. Its answer could be , depending on the procedure by which the information "at least one of them is a boy" was obtained. The ambiguity, depending on the exact wording and possible assumptions, was confirmed by Maya Ba ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monty Hall Problem
The Monty Hall problem is a brain teaser, in the form of a probability puzzle, loosely based on the American television game show ''Let's Make a Deal'' and named after its original host, Monty Hall. The problem was originally posed (and solved) in a letter by Steve Selvin to the '' American Statistician'' in 1975. It became famous as a question from reader Craig F. Whitaker's letter quoted in Marilyn vos Savant's "Ask Marilyn" column in ''Parade'' magazine in 1990: Vos Savant's response was that the contestant should switch to the other door. Under the standard assumptions, the switching strategy has a probability of winning the car, while the strategy that remains with the initial choice has only a probability. When the player first makes their choice, there is a chance that the car is behind one of the doors not chosen. This probability does not change after the host reveals a goat behind one of the unchosen doors. When the host provides information about the 2 unchosen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |