|
Barnard's Test
In statistics, Barnard’s test is an exact test used in the analysis of contingency tables with one margin fixed. Barnard’s tests are really a class of hypothesis tests, also known as unconditional exact tests for two independent binomials. These tests examine the association of two categorical variables and are often a more powerful alternative than Fisher's exact test for contingency tables. While first published in 1945 by G.A. Barnard, the test did not gain popularity due to the computational difficulty of calculating the value and Fisher’s specious disapproval. Nowadays, even for sample sizes ''n'' ~ 1 million, computers can often implement Barnard’s test in a few seconds or less. Purpose and scope Barnard’s test is used to test the independence of rows and columns in a contingency table. The test assumes each response is independent. Under independence, there are three types of study designs that yield a table, and Barnard's test applies to the second t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Central Limit Theorem
In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the Probability distribution, distribution of a normalized version of the sample mean converges to a Normal distribution#Standard normal distribution, standard normal distribution. This holds even if the original variables themselves are not Normal distribution, normally distributed. There are several versions of the CLT, each applying in the context of different conditions. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions. This theorem has seen many changes during the formal development of probability theory. Previous versions of the theorem date back to 1811, but in its modern form it was only precisely stated as late as 1920. In statistics, the CLT can be stated as: let X_1, X_2, \dots, X_n denote a Sampling ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Progress In Nuclear Energy
''Progress in Nuclear Energy'' is a monthly peer-reviewed scientific journal covering research on nuclear energy and nuclear science. It was established in 1977 and is published by Elsevier. The current editors-in-chief are Yousry Azmy (North Carolina State University), Simon Middleburgh (Bangor University), and Guanghui Su (Xi'an Jiaotong University). Abstracting and indexing The journal is abstracted and indexed in: * Chemical Abstracts Service * Science Citation Index Expanded * Current Contents/Engineering, Computing & Technology * Scopus According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 2.461. References External links * Energy and fuel journals Elsevier academic journals English-lang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Uniformly Most Powerful Test
In statistical hypothesis testing, a uniformly most powerful (UMP) test is a hypothesis test which has the greatest power 1 - \beta among all possible tests of a given size ''α''. For example, according to the Neyman–Pearson lemma, the likelihood-ratio test is UMP for testing simple (point) hypotheses. Setting Let X denote a random vector (corresponding to the measurements), taken from a parametrized family of probability density functions or probability mass functions f_(x), which depends on the unknown deterministic parameter \theta \in \Theta. The parameter space \Theta is partitioned into two disjoint sets \Theta_0 and \Theta_1. Let H_0 denote the hypothesis that \theta \in \Theta_0, and let H_1 denote the hypothesis that \theta \in \Theta_1. The binary test of hypotheses is performed using a test function \varphi(x) with a reject region R (a subset of measurement space). :\varphi(x) = \begin 1 & \text x \in R \\ 0 & \text x \in R^c \end meaning that H_1 is in force if t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Boschloo's Test
Boschloo's test is a statistical hypothesis test for analysing 2x2 contingency tables. It examines the association of two Bernoulli distributed random variables and is a uniformly more powerful alternative to Fisher's exact test. It was proposed in 1970 by R. D. Boschloo. Setting A 2 × 2 contingency table visualizes \ n\ independent observations of two binary variables \ A\ and \ B\ : : \begin & B = 1 & B = 0 & \mbox\\ \hline A = 1 & x_ & x_ & n_1 \\ A = 0 & x_ & x_ & n_0 \\ \hline \mbox & s_1 & s_0 & n\\ \end The probability distribution of such tables can be classified into three distinct cases. # The row sums \ n_1\ , n_0\ and column sums \ s_1\ , s_0\ are fixed in advance and not random. Then all \ x_\ are determined by \ x_ ~. If \ A\ and \ B\ are independent, \ x_\ follows a hypergeometric distribution with parameters \ n\ , n_1\ , s_1\ : \ x_\ \sim\ \mbox(\ n\ , n_1\ , s_1\ ) ~. # The row sums \ n_1\ , n_0\ are fixed in advance but the column sums \ s_ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Experimental Design
The design of experiments (DOE), also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation. In its simplest form, an experiment aims at predicting the outcome by introducing a change of the preconditions, which is represented by one or more independent variables, also referred to as "input variables" or "predictor variables." The change in one or more independent variables is generally hypothesized to result in a change in one or more dependent variables, also referred to as "output variables" or "response variables." The experimental design may also identify c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Type I And Type II Errors
Type I error, or a false positive, is the erroneous rejection of a true null hypothesis in statistical hypothesis testing. A type II error, or a false negative, is the erroneous failure in bringing about appropriate rejection of a false null hypothesis. Type I errors can be thought of as errors of commission, in which the status quo is erroneously rejected in favour of new, misleading information. Type II errors can be thought of as errors of omission, in which a misleading status quo is allowed to remain due to failures in identifying it as such. For example, if the assumption that people are ''innocent until proven guilty'' were taken as a null hypothesis, then proving an innocent person as guilty would constitute a Type I error, while failing to prove a guilty person as guilty would constitute a Type II error. If the null hypothesis were inverted, such that people were by default presumed to be ''guilty until proven innocent'', then proving a guilty person's innocence would ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Hypergeometric
In mathematics, the Gaussian or ordinary hypergeometric function 2''F''1(''a'',''b'';''c'';''z'') is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation. For systematic lists of some of the many thousands of published identities involving the hypergeometric function, see the reference works by and . There is no known system for organizing all of the identities; indeed, there is no known algorithm that can generate all identities; a number of different algorithms are known that generate different series of identities. The theory of the algorithmic discovery of identities remains an active research topic. History The term "hypergeometric series" was first used by John Wallis in his 1655 book ''Arithmetica Infinitoru ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Ancillary Statistic
In statistics, ancillarity is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. An ancillary statistic has the same distribution regardless of the value of the parameters and thus provides no information about them. It is opposed to the concept of a complete statistic which contains no ancillary information. It is closely related to the concept of a sufficient statistic which contains all of the information that the dataset provides about the parameters. A ancillary statistic is a specific case of a pivotal quantity that is computed only from the data and not from the parameters. They can be used to construct prediction intervals. They are also used in connection with Basu's theorem to prove independence between statistics. This concept was first introduced by Ronald Fisher in the 1920s, but its formal definition was only provided in 1964 by Debabrata Basu. Examples Suppose ''X''1, ..., ''X''''n'' are independent a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Nuisance Parameter
In statistics, a nuisance parameter is any parameter which is unspecified but which must be accounted for in the hypothesis testing of the parameters which are of interest. The classic example of a nuisance parameter comes from the normal distribution, a member of the location–scale family. For at least one normal distribution, the variance(s), ''σ2'' is often not specified or known, but one desires to hypothesis test on the mean(s). Another example might be linear regression with unknown variance in the explanatory variable (the independent variable): its variance is a nuisance parameter that must be accounted for to derive an accurate interval estimate of the regression slope, calculate p-values, hypothesis test on the slope's value; see regression dilution. Nuisance parameters are often scale parameters, but not always; for example in errors-in-variables models, the unknown true location of each observation is a nuisance parameter. A parameter may also cease to be a " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
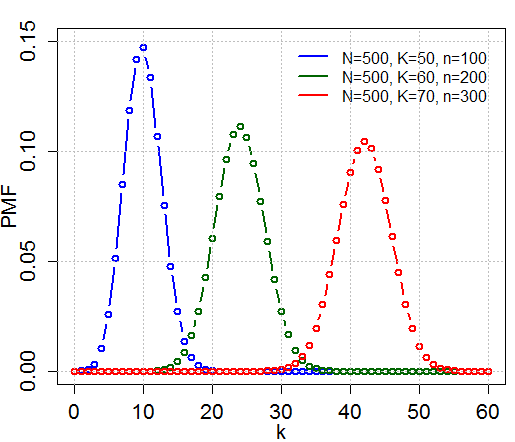 |
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a Probability distribution#Discrete probability distribution, discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite Statistical population, population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of Binary variable, two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |