|
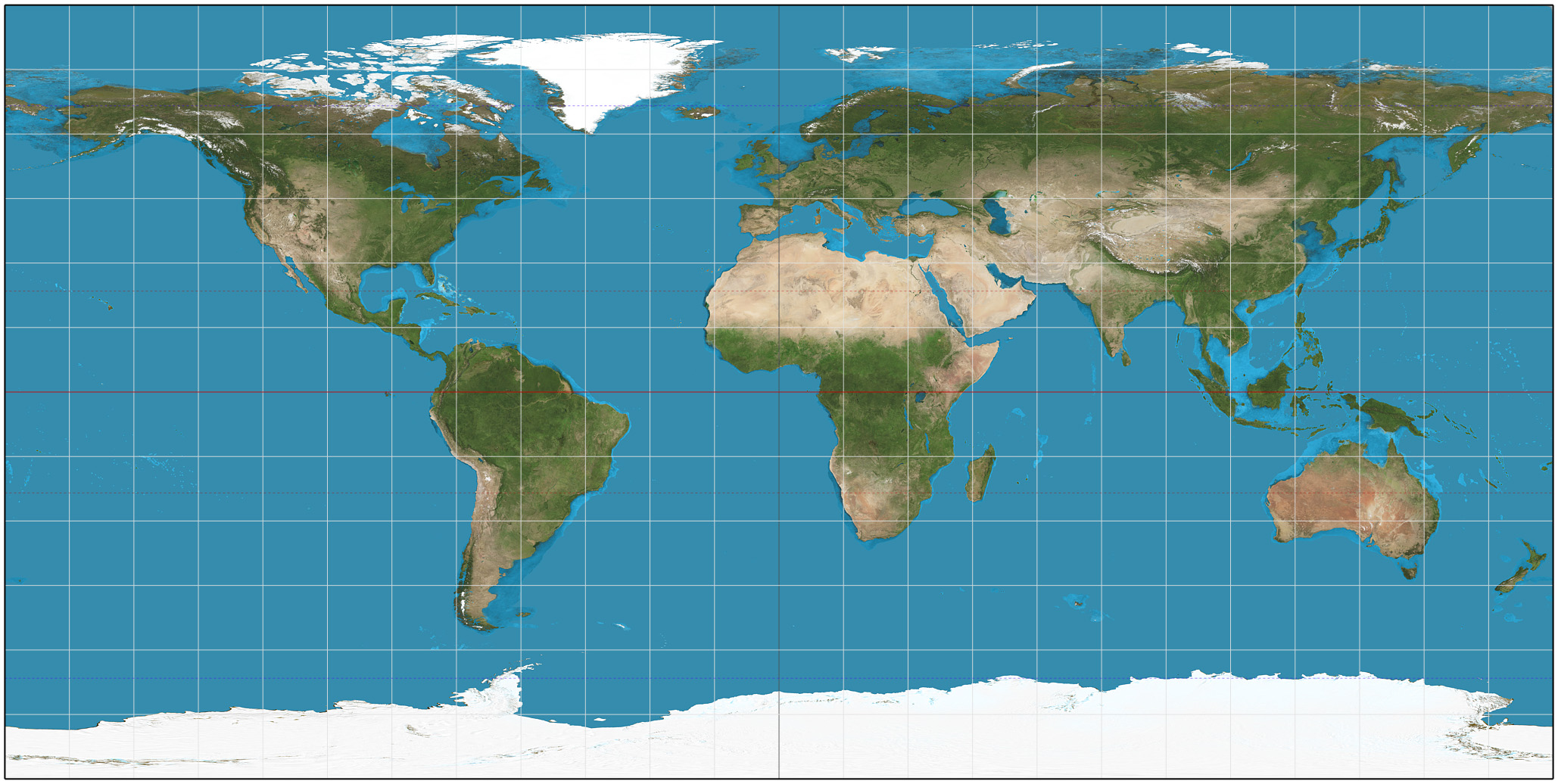
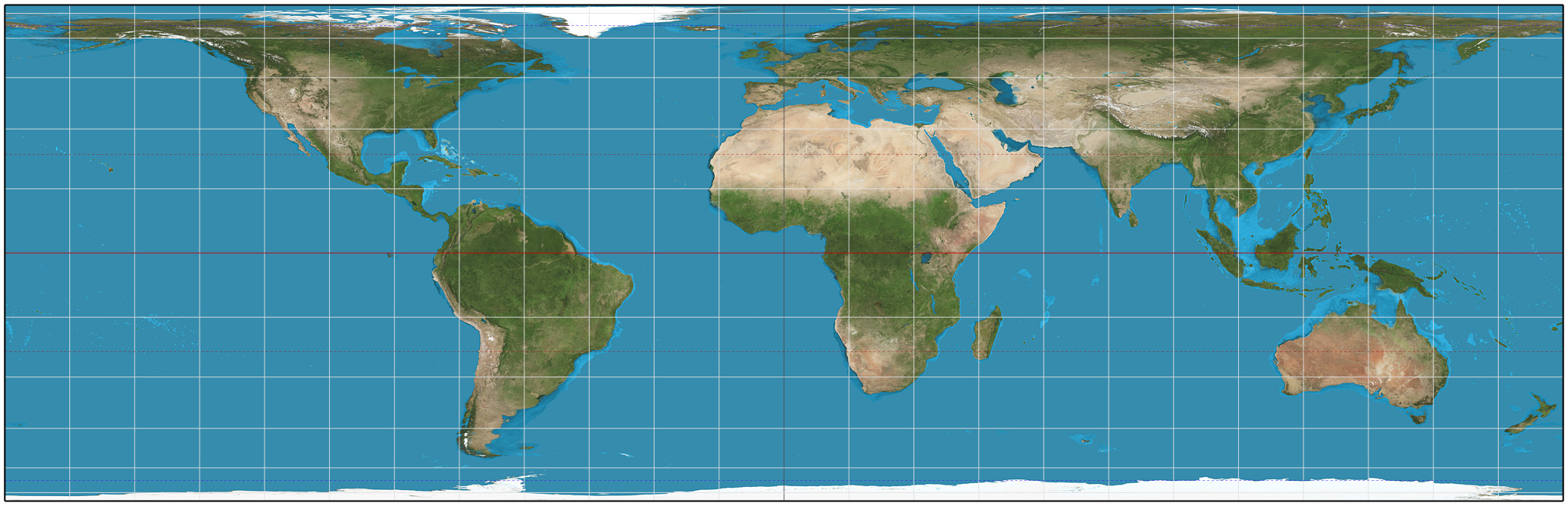
AuthaGraph Projection
AuthaGraph is an approximately equal-area world map projection invented by Japanese architect Hajime Narukawa in 1999. The map is made by equally dividing a spherical surface into 96 triangles, transferring it to a tetrahedron while maintaining area proportions, and unfolding it in the form of a rectangle: it is a polyhedral map projection. The map substantially preserves sizes and shapes of all continents and oceans while it reduces distortions of their shapes, as inspired by the Dymaxion map. The projection does not have some of the major distortions of the Mercator projection, like the expansion of countries in far northern latitudes, and allows for Antarctica to be displayed accurately and in whole. Triangular world maps are also possible using the same method. The name is derived from " authalic" and "graph". The method used to construct the projection ensures that the 96 regions of the sphere that are used to define the projection each have the correct area, but the pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection AuthaGraph
Projection or projections may refer to: Physics * Projection (physics), the action/process of light, heat, or sound reflecting from a surface to another in a different direction * The display of images by a projector Optics, graphics, and cartography * Map projection, reducing the surface of a three-dimensional planet to a flat map * Graphical projection, the production of a two-dimensional image of a three-dimensional object Chemistry * Fischer projection, a two-dimensional representation of a three-dimensional organic molecule * Haworth projection, a way of writing a structural formula to represent the cyclic structure of monosaccharides * Natta projection, a way to depict molecules with complete stereochemistry in two dimensions in a skeletal formula * Newman projection, a visual representation of a chemical bond from front to back Mathematics * Projection (mathematics), any of several different types of geometrical mappings ** Projection (linear algebra), a linear transf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
National Museum Of Emerging Science And Innovation
The , simply known as the , is a museum created by Japan's Science and Technology Agency. It was opened in 2001. It is situated in a purpose-built building in the Odaiba District of Tokyo. It can be reached by the Yurikamome driverless fully automated transit system from downtown Tokyo in about 20 minutes. Permanent Exhibition “Explore the frontiers” “Explore the frontiers” zone explores, on a variety of scales, the construction of the world, the Earthʼs environment and all the life nurtured within, as well as the Solar System and the universe. Looking back on the universeʼs history that spans 13.8 billion years, how did humans begin, and how are people living and interacting with the world around us? By taking a scientific viewpoint, people can think from a broad perspective on which path people should follow to the future. Permanent Exhibition “Create your future” “Create your future”zone illustrates desirable societies and lifestyles, and considers ideas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
1999 Introductions
1999 was designated as the International Year of Older Persons. Events January * January 1 – The euro currency is established and the European Central Bank assumes its full powers. * January 3 – The Mars Polar Lander is launched by NASA. * January 25 – The 6.2 Colombia earthquake hits western Colombia, killing at least 1,900 people. February * February 7 – Abdullah II inherits the throne of Jordan, following the death of his father King Hussein. * February 11 – Pluto moves along its eccentric orbit further from the Sun than Neptune. It had been nearer than Neptune since 1979, and will become again in 2231. * February 12 – U.S. President Bill Clinton is acquitted in impeachment proceedings in the United States Senate. * February 16 ** In Uzbekistan, an apparent assassination attempt against President Islam Karimov takes place at government headquarters. ** Across Europe, Kurdish protestors take over embassies and hold hostages a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyhedral Map Projection
A polyhedral map projection is a map projection based on a spherical polyhedron. Typically, the polyhedron is overlaid on the globe, and each face of the polyhedron is transformed to a polygon or other shape in the plane. The best-known polyhedral map projection is Buckminster Fuller's Dymaxion map. When the spherical polyhedron faces are transformed to the faces of an ordinary polyhedron instead of laid flat in a plane, the result is a polyhedral globe. Often the polyhedron used is a Platonic solid or Archimedean solid. However, other polyhedra can be used: the AuthaGraph projection makes use of a polyhedron with 96 faces, and the myriahedral projection allows for an arbitrary large number of faces. Although interruptions between faces are common, and more common with an increasing number of faces, some maps avoid them: the Lee conformal projection only has interruptions at its border, and the AuthaGraph projection scales its faces so that the map fills a rectangle without int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peirce Quincuncial Projection
The Peirce quincuncial projection is the conformal map projection from the sphere to an unfolded square dihedron, developed by Charles Sanders Peirce in 1879. Each octant (solid geometry), octant projects onto an Special right triangle#45-45-90 triangle, isosceles right triangle, and these are arranged into a square. The name ''quincuncial'' refers to this arrangement: the north pole at the center and quarters of the south pole in the corners form a quincunx pattern like the pips on the ''five'' face of a traditional dice, die. The projection has the distinctive property that it forms a seamless square tiling of the plane, conformal except at four Mathematical singularity, singular points along the equator. Typically the projection is square and oriented such that the north pole lies at the center, but Guyou hemisphere-in-a-square projection, an oblique aspect in a rectangle was proposed by Émile Guyou in 1887, and Adams hemisphere-in-a-square_projection, a transverse aspect wa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lee Conformal World In A Tetrahedron
The Lee conformal world in a tetrahedron is a polyhedral, conformal map projection that projects the globe onto a tetrahedron using Dixon elliptic functions. It is conformal everywhere except for the four singularities at the vertices of the polyhedron. Because of the nature of polyhedra, this map projection can be tessellated infinitely in the plane. It was developed by Laurence Patrick Lee in 1965. Supplement No. 1 t''The Canadian Cartographer'' 13 Coordinates from a spherical datum can be transformed into Lee conformal projection coordinates with the following formulas, where \lambda is the longitude and \varphi the latitude: : 2 \operatornamew\,\operatornamew = 2^\exp(i\lambda) \tan\bigl(\tfrac14\pi - \tfrac12\varphi\bigr) where : w = x + y i and sm and cm are Dixon elliptic functions. Since there is no elementary expression for these functions, Lee suggests using the 28th-degree MacLaurin series. See also * List of map projections * AuthaGraph projection, anot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nebraska Examiner
States Newsroom is a nonprofit news network in the United States. Its newsrooms focus mostly on state politics. States Newsroom grew out of NC Policy Watch, a progressive think tank founded in 2004 by Chris Fitzsimon, who said it "is sort of the model for the news sites we support". He is States Newsroom's current president. In 2017, the project expanded, using the liberal group the Hopewell Fund as an incubator until 2019 when States Newsroom became an independent 501(c)(3) nonprofit. Organization States Newsroom provides funding, human resources, and digital support to journalists in the state newsrooms. It typically has 4-6 journalists per newsroom'''' and allows its articles to be republished for free under a Creative Commons license.'''' States Newsroom accepts no corporate donations and has publicly shared the names of all donors contributing $1,000 or more since becoming a 501(c)(3) in 2019. The progressive Wyss Foundation gave $1 million to States Newsroom in 202 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Equal-area Projection
In cartography, the normal cylindrical equal-area projection is a family of Map projection#Normal cylindrical, normal cylindrical, equal-area projection, equal-area map projections. History The invention of the Lambert cylindrical equal-area projection is attributed to the Switzerland, Swiss mathematician Johann Heinrich Lambert in 1772. Variations of it appeared over the years by inventors who stretched the height of the Lambert and compressed the width commensurately in various ratios. Description The projection: * is Map_projection#Cylindrical, cylindrical, that means it has a cylindrical projection surface * is normal, that means it has a normal Map projection#Aspect, aspect * is an equal-area projection, that means any two areas in the map have the same relative size compared to their size on the sphere. The term "normal cylindrical projection" is used to refer to any projection in which Meridian (geography), meridians are mapped to equally spaced vertical lines and cir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gall–Peters Projection
The Gall–Peters projection is a rectangular, Equal-area projection, equal-area map projection. Like all equal-area projections, it distorts most shapes. It is a cylindrical equal-area projection with latitudes 45° north and south as the regions on the map that have no distortion. The projection is named after James Gall and Arno Peters. Gall described the projection in 1855 at a science convention and published a paper on it in 1885. Peters brought the projection to a wider audience beginning in the early 1970s through his "Peters World Map". The name "Gall–Peters projection" was first used by Arthur H. Robinson in a pamphlet put out by the American Cartographic Association in 1986.American Cartographic Association's Committee on Map Projections, 1986. ''Which Map is Best'' p. 12. Falls Church: American Congress on Surveying and Mapping. The Gall–Peters projection achieved notoriety in the late 20th century as the centerpiece of a controversy about the political implication ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jim Pillen
James Douglas Pillen (born December 31, 1955) is an American politician, veterinarian, and livestock producer serving as the 41st and current governor of Nebraska since 2023. A member of the Republican Party, Pillen served on the University of Nebraska Board of Regents from 2013 to 2023. Early life and education Pillen was born in Columbus, Nebraska, to Dale and Dorothy Pillen. His parents were farmers. Dale Pillen served in the United States Army during the Korean War. He died at a Columbus hospital in 1999 at age 72. His grandfather immigrated to the United States from Germany and later served in the U.S. military during World War I. After graduating from Lakeview Junior-Senior High School in 1974, Pillen earned a Bachelor of Science degree in animal science from the University of Nebraska–Lincoln and a Doctor of Veterinary Medicine from the Kansas State University College of Veterinary Medicine. From 1975 to 1978, Pillen was a defensive back for the Nebraska Cornhus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nebraska
Nebraska ( ) is a landlocked U.S. state, state in the Midwestern United States, Midwestern region of the United States. It borders South Dakota to the north; Iowa to the east and Missouri to the southeast, both across the Missouri River; Kansas to the south; Colorado to the southwest; and Wyoming to the west. Nebraska is the List of U.S. states and territories by area, 16th-largest state by land area, with just over . With a population of over 2 million as of 2024, it is the List of U.S. states and territories by population, 38th-most populous state and the List of states and territories of the United States by population density, eighth-least densely populated. Its List of capitals in the United States, capital is Lincoln, Nebraska, Lincoln, and its List of municipalities in Nebraska, most populous city is Omaha, Nebraska, Omaha, which is on the Missouri River. Nebraska was admitted into the United States in 1867, two years after the end of the American Civil War. The Nebras ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |