|
Astronomical Unit
The astronomical unit (symbol: au or AU) is a unit of length defined to be exactly equal to . Historically, the astronomical unit was conceived as the average Earth-Sun distance (the average of Earth's aphelion and perihelion), before its modern redefinition in 2012. The astronomical unit is used primarily for measuring distances within the Solar System or around other stars. It is also a fundamental component in the definition of another unit of astronomical length, the parsec. One au is approximately equivalent to 499 light-seconds. History of symbol usage A variety of unit symbols and abbreviations have been in use for the astronomical unit. In a 1976 resolution, the International Astronomical Union (IAU) had used the symbol ''A'' to denote a length equal to the astronomical unit. In the astronomical literature, the symbol AU is common. In 2006, the International Bureau of Weights and Measures (BIPM) had recommended ua as the symbol for the unit, from the French ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomical System Of Units
The astronomical system of units, formerly called the IAU (1976) System of Astronomical Constants, is a system of measurement developed for use in astronomy. It was adopted by the International Astronomical Union (IAU) in 1976 via Resolution No. 1, and has been significantly updated in 1994 and 2009 (see Astronomical constant). The system was developed because of the difficulties in measuring and expressing astronomical data in International System of Units (SI units). In particular, there is a huge quantity of very precise data relating to the positions of objects within the Solar System that cannot conveniently be expressed or processed in SI units. Through a number of modifications, the astronomical system of units now explicitly recognizes the consequences of general relativity, which is a necessary addition to the International System of Units in order to accurately treat astronomical data. The astronomical system of units is a tridimensional system, in that it defines uni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scientific Journal
In academic publishing, a scientific journal is a periodical publication designed to further the progress of science by disseminating new research findings to the scientific community. These journals serve as a platform for researchers, scholars, and scientists to share their latest discoveries, insights, and methodologies across a multitude of scientific disciplines. Unlike professional or trade magazines, the articles are mostly written by scientists rather than staff writers employed by the journal. Scientific journals are characterized by their rigorous peer review process, which aims to ensure the validity, reliability, and quality of the published content. In peer review, submitted articles are reviewed by active scientists (peers) to ensure scientific rigor. With origins dating back to the 17th century, the publication of scientific journals has evolved significantly, advancing scientific knowledge, fostering academic discourse, and facilitating collaboration within ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's ''Principia'' (1687). The name celestial mechanics is more recent than that. Newton wrote that the field should be called "rational mechanics". The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term ''celestial mechanics''. Prior to Kepler, there was little connection between exact, quantitative prediction of planetary positions, using geometrical or numerical techniques, and contemporary discussions of the physical causes of the planets' motion. Laws of planetary motion Johannes Kepler was the first to closely integrate the predictive geometrical a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Relativity
The theory of relativity usually encompasses two interrelated physics theories by Albert Einstein: special relativity and general relativity, proposed and published in 1905 and 1915, respectively. Special relativity applies to all physical phenomena in the absence of gravity. General relativity explains the law of gravitation and its relation to the forces of nature. It applies to the cosmological and astrophysical realm, including astronomy. The theory transformed theoretical physics and astronomy during the 20th century, superseding a 200-year-old theory of mechanics created primarily by Isaac Newton. It introduced concepts including 4-dimensional spacetime as a unified entity of space and time, relativity of simultaneity, kinematic and gravitational time dilation, and length contraction. In the field of physics, relativity improved the science of elementary particles and their fundamental interactions, along with ushering in the nuclear age. With relativity, cosmolog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence formula , which arises from special relativity, has been called "the world's most famous equation". He received the 1921 Nobel Prize in Physics for . Born in the German Empire, Einstein moved to Switzerland in 1895, forsaking his German citizenship (as a subject of the Kingdom of Württemberg) the following year. In 1897, at the age of seventeen, he enrolled in the mathematics and physics teaching diploma program at the Swiss ETH Zurich, federal polytechnic school in Zurich, graduating in 1900. He acquired Swiss citizenship a year later, which he kept for the rest of his life, and afterwards secured a permanent position at the Swiss Patent Office in Bern. In 1905, he submitted a successful PhD dissertation to the University of Zurich. In 19 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different sightline, lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to perspective (graphical), foreshortening, nearby objects show a larger parallax than farther objects, so parallax can be used to determine distances. To measure large distances, such as the distance of a planet or a star from Earth, astronomers use the principle of parallax. Here, the term ''Stellar parallax, parallax'' is the semi-angle of inclination between two sight-lines to the star, as observed when Earth is on opposite sides of the Sun in its orbit. These distances form the lowest rung of what is called "the cosmic distance ladder", the first in a succession of methods by which astronomers determine the distances to celestial objects, serving as a basis for other distance measurements in astronomy forming the higher rungs of the ladder. Because parallax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perihelion And Aphelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values. Apsides pertaining to orbits around different bodies have distinct names to differentiate themselves from other apsides. Apsides pertaining to geocentric orbits, orbits around the Earth, are at the farthest point called the ''apogee'', and at the nearest point the ''perigee'', like with orbits of satellites and the Moon around Earth. Apsides pertaining to orbits around the Sun are named ''aphelion'' for the farthest and ''perihelion'' for the nearest point in a heliocentric orbit. Earth's two apsides are the farthest point, ''aphelion'', and the nearest point, ''perihelion'', of its orbit around the host Sun. The terms ''aphelion'' and ''perihelion'' apply in the same way to the orbits of Jupiter and the other planets, the comets, and the asteroids of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line Segment
In geometry, a line segment is a part of a line (mathematics), straight line that is bounded by two distinct endpoints (its extreme points), and contains every Point (geometry), point on the line that is between its endpoints. It is a special case of an ''arc (geometry), arc'', with zero curvature. The length of a line segment is given by the Euclidean distance between its endpoints. A closed line segment includes both endpoints, while an open line segment excludes both endpoints; a half-open line segment includes exactly one of the endpoints. In geometry, a line segment is often denoted using an overline (vinculum (symbol), vinculum) above the symbols for the two endpoints, such as in . Examples of line segments include the sides of a triangle or square. More generally, when both of the segment's end points are vertices of a polygon or polyhedron, the line segment is either an edge (geometry), edge (of that polygon or polyhedron) if they are adjacent vertices, or a diagonal. Wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
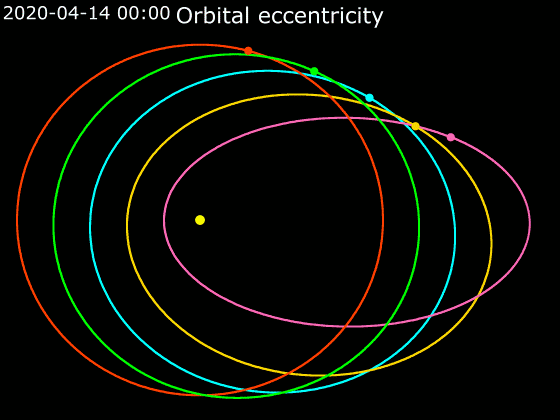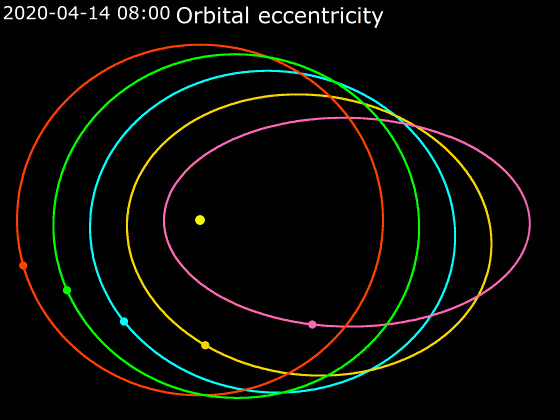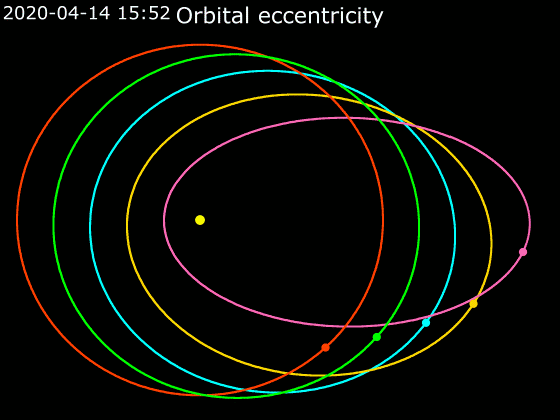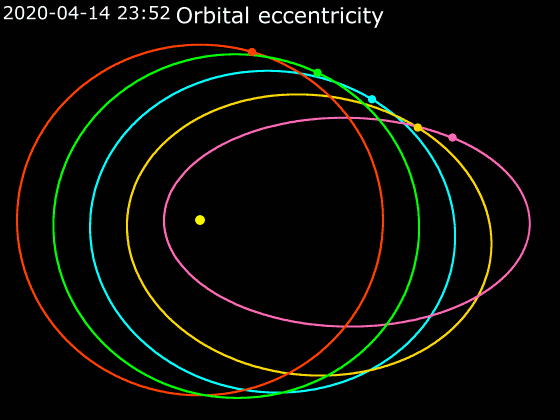
Elliptic Orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some orbits have been referred to as "elongated orbits" if the eccentricity is "high" but that is not an explanatory term. For the simple two body problem, all orbits are ellipses. In a gravitational two-body problem, both bodies follow similar elliptical orbits with the same orbital period around their common barycenter. The relative position of one body with respect to the other also follows an elliptic orbit. Examples of elliptic orbits include Hohmann transfer orbits, Molniya orbits, and tundra orbits. Velocity Under standard assumptions, no other forces acting except two spherically symmetrical bodies (m_1) and (m_2), the orbital speed (v\,) of one body traveling along an elliptical orbit can be computed from the vis-viva equation as: :v = \sqrt where: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-major Axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the longest semidiameter or one half of the major axis, and thus runs from the centre, through a focus, and to the perimeter. The semi-minor axis (minor semiaxis) of an ellipse or hyperbola is a line segment that is at right angles with the semi-major axis and has one end at the center of the conic section. For the special case of a circle, the lengths of the semi-axes are both equal to the radius of the circle. The length of the semi-major axis of an ellipse is related to the semi-minor axis's length through the eccentricity and the semi-latus rectum \ell, as follows: The semi-major axis of a hyperbola is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the ce ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in which the two focal points are the same. The elongation of an ellipse is measured by its eccentricity (mathematics), eccentricity e, a number ranging from e = 0 (the Limiting case (mathematics), limiting case of a circle) to e = 1 (the limiting case of infinite elongation, no longer an ellipse but a parabola). An ellipse has a simple algebraic solution for its area, but for Perimeter of an ellipse, its perimeter (also known as circumference), Integral, integration is required to obtain an exact solution. The largest and smallest diameters of an ellipse, also known as its width and height, are typically denoted and . An ellipse has four extreme points: two ''Vertex (geometry), vertices'' at the endpoints of the major axis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth's Orbit
Earth orbits the Sun at an astronomical unit, average distance of , or 8.317 light-second, light-minutes, in a retrograde and prograde motion, counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes days (1 sidereal year), during which time Earth has traveled .Jean Meeus, ''Astronomical Algorithms'' 2nd ed, (Richmond, VA: Willmann-Bell, 1998) 238. See Ellipse#Circumference. The formula by Ramanujan is accurate enough. Ignoring the influence of other Solar System bodies, Earth's orbit, also called Earth's revolution, is an ellipse with the Earth–Sun barycenter as one focus (geometry), focus with a current orbital eccentricity, eccentricity of 0.0167. Since this value is close to zero, the center of the orbit is relatively close to the center of the Sun (relative to the size of the orbit). As seen from Earth, the planet's orbital prograde motion makes the Sun diurnal motion, appear to move with respect to fixed stars, other star ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |