|
Arrow's Impossibility Theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Arrow showed no such rule can satisfy the independence of irrelevant alternatives axiom. This is the principle that a choice between two alternatives and should not depend on the quality of some third, unrelated option, . The result is often cited in discussions of voting rules, where it shows no ranked voting rule to eliminate the spoiler effect. This result was first shown by the Marquis de Condorcet, whose voting paradox showed the impossibility of logically-consistent majority rule; Arrow's theorem generalizes Condorcet's findings to include non-majoritarian rules like collective leadership or consensus decision-making. While the impossibility theorem shows all ranked voting rules must have spoilers, the frequency of spoilers differs dramatically by rule. Plurality-rule me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice Theory
Social choice theory is a branch of welfare economics that extends the Decision theory, theory of rational choice to collective decision-making. Social choice studies the behavior of different mathematical procedures (social welfare function, social welfare functions) used to combine individual preferences into a coherent whole.Amartya Sen (2008). "Social Choice". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> It contrasts with political science in that it is a Normative economics, normative field that studies how a society can make good decisions, whereas political science is a Positive economics, descriptive field that observes how societies actually do make decisions. While social choice began as a branch of economics and decision theory, it has since received substantial contributions from mathematics, philosophy, political science, and game theory. Real-world examples of social choice rules include constitution, constitutions and Parliamentary ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instant-runoff Voting
Instant-runoff voting (IRV; ranked-choice voting (RCV), preferential voting, alternative vote) is a single-winner ranked voting election system where Sequential loser method, one or more eliminations are used to simulate Runoff (election), runoff elections. When no candidate has a majority of the votes in the first round of counting, each following round eliminates the candidate with the fewest First-preference votes, first-preferences (among the remaining candidates) and transfers their votes if possible. This continues until one candidate accumulates a majority of the votes still in play. Instant-runoff voting falls under the plurality-based voting-rule family, in that under certain conditions the candidate with the least votes is eliminated, making use of secondary rankings as contingency votes. Thus it is related to the Runoff election, two-round runoff system and the exhaustive ballot. IRV could also be seen as a single-winner equivalent of Single transferable vote, sin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approval Voting
Approval voting is a single-winner rated voting system where voters can approve of all the candidates as they like instead of Plurality voting, choosing one. The method is designed to eliminate vote-splitting while keeping election administration simple and Summability criterion, easy-to-count (requiring only a single score for each candidate). Approval voting has been used in both organizational and political elections to improve representativeness and voter satisfaction. Critics of approval voting have argued the simple ballot format is a disadvantage, as it forces a Dichotomous preferences, binary choice for each candidate (instead of the expressive grades of other rated voting rules). Effect on elections Research by Social choice theory, social choice theorists Steven Brams and Dudley R. Herschbach found that approval voting would increase voter participation, prevent minor-party candidates from being spoiler effect, spoilers, and reduce negative campaigning. Brams' researc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Score Voting
Score voting, sometimes called range voting, is an electoral system for single-seat elections. Voters give each candidate a numerical score, and the candidate with the highest average score is elected. Score voting includes the well-known approval voting (used to calculate approval ratings), but also lets voters give partial (in-between) approval ratings to candidates. Usage Political use Historical A crude form of score voting was used in some elections in ancient Sparta, by measuring how loudly the crowd shouted for different candidates. This has a modern-day analog of using clapometers in some television shows and the judging processes of some athletic competitions. Beginning in the 13th century, the Republic of Venice elected the Doge of Venice using a multi-stage process with multiple rounds of score voting. This may have contributed to the Republic's longevity, being partly responsible for its status as the longest-lived democracy in world history. Score voting w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardinal Utility
In economics, a cardinal utility expresses not only which of two outcomes is preferred, but also the intensity of preferences, i.e. ''how much'' better or worse one outcome is compared to another. In consumer choice theory, economists originally attempted to replace cardinal utility with the apparently weaker concept of ordinal utility. Cardinal utility appears to impose the assumption that levels of absolute satisfaction exist, so magnitudes of increments to satisfaction can be compared across different situations. However, economists in the 1940s proved that under mild conditions, ordinal utilities imply cardinal utilities. This result is now known as the von Neumann–Morgenstern utility theorem; many similar utility representation theorems exist in other contexts. History In 1738, Daniel Bernoulli was the first to theorize about the marginal value of money. He assumed that the value of an additional amount is inversely proportional to the pecuniary possessions which a per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Identity Of Indiscernibles
The identity of indiscernibles is an ontological principle that states that there cannot be separate objects or entities that have all their properties in common. That is, entities ''x'' and ''y'' are identical if every predicate possessed by ''x'' is also possessed by ''y'' and vice versa. It states that no two distinct things (such as snowflakes) can be exactly alike, but this is intended as a metaphysical principle rather than one of natural science. A related principle is the indiscernibility of identicals, discussed below. A form of the principle is attributed to the German philosopher Gottfried Wilhelm Leibniz. While some think that Leibniz's version of the principle is meant to be only the indiscernibility of identicals, others have interpreted it as the conjunction of the identity of indiscernibles and the indiscernibility of identicals (the converse principle). Because of its association with Leibniz, the indiscernibility of identicals is sometimes known as Leibniz's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rated Voting
Rated, evaluative, graded, or cardinal voting rules are a class of voting methods that allow voters to state how strongly they support a candidate, by giving each one a grade on a separate scale. The distribution of ratings for each candidate—i.e. the percentage of voters who assign them a particular score—is called their merit profile. For example, if candidates are graded on a 4-point scale, one candidate's merit profile may be 25% on every possible rating (1, 2, 3, and 4), while a perfect candidate would have a merit profile where 100% of voters assign them a score of 4. Since rated methods allow the voters to express how strongly they support a candidate, these methods are not covered by Arrow's impossibility theorem, and their resistance to the spoiler effect becomes a more complex matter. Some rated methods are immune to the spoiler effect when every voter rates the candidates on an absolute scale, but they are not when the voters' rating scales change based on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
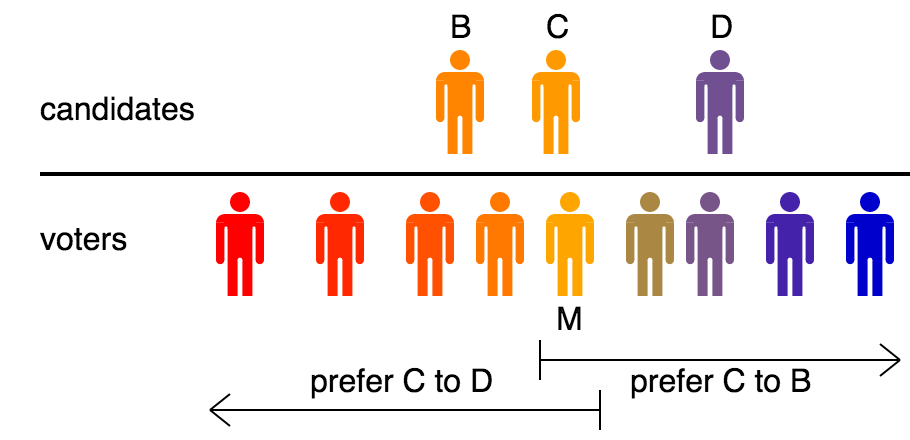
Black's Median Voter Theorem
In political science and social choice, Black's median voter theorem says that if voters and candidates are distributed along a political spectrum, any voting method compatible with majority-rule will elect the candidate preferred by the median voter. The median voter theorem thus shows that under a realistic model of voter behavior, Arrow's theorem does not apply, and rational choice is possible for societies. The theorem was first derived by Duncan Black in 1948, and independently by Kenneth Arrow. Voting rules without this median voter property, like ranked choice voting, plurality, and plurality-with-primaries have a center-squeeze effect that encourages candidates to take more extreme positions than the population would prefer. Similar median voter theorems exist for rules like score voting and approval voting when voters are either strategic and informed or if voters' ratings of candidates fall linearly with ideological distance. An immediate consequence of Black's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical modeling''. Mathematical models are used in applied mathematics and in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). It can also be taught as a subject in its own right. The use of mathematical models to solve problems in business or military operations is a large part of the field of operations research. Mathematical models are also used in music, linguistics, and philosophy (for example, intensively in analytic philosophy). A model may help to explain a system and to study the effects of different components, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Tie
In social choice theory, Condorcet's voting paradox is a fundamental discovery by the Marquis de Condorcet that majority rule is inherently self-contradictory. The result implies that it is logically impossible for any voting system to guarantee that a winner will have support from a majority of voters; for example, there can be rock-paper-scissors scenarios where a majority of voters will prefer A to B, B to C, and also C to A, even if every voter's individual preferences are rational and avoid self-contradiction. Examples of Condorcet's paradox are called Condorcet cycles or cyclic ties. In such a cycle, every possible choice is rejected by the electorate in favor of another alternative, who is preferred by more than half of all voters. Thus, any attempt to ground social decision-making in majoritarianism must accept such self-contradictions (commonly called spoiler effects). Systems that attempt to do so, while minimizing the rate of such self-contradictions, are called Condo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arrow's Impossibility Theorem
Arrow's impossibility theorem is a key result in social choice theory showing that no ranked-choice procedure for group decision-making can satisfy the requirements of rational choice. Specifically, Arrow showed no such rule can satisfy the independence of irrelevant alternatives axiom. This is the principle that a choice between two alternatives and should not depend on the quality of some third, unrelated option, . The result is often cited in discussions of voting rules, where it shows no ranked voting rule to eliminate the spoiler effect. This result was first shown by the Marquis de Condorcet, whose voting paradox showed the impossibility of logically-consistent majority rule; Arrow's theorem generalizes Condorcet's findings to include non-majoritarian rules like collective leadership or consensus decision-making. While the impossibility theorem shows all ranked voting rules must have spoilers, the frequency of spoilers differs dramatically by rule. Plurality-rule me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condorcet Method
A Condorcet method (; ) is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, whenever there is such a candidate. A candidate with this property, the ''pairwise champion'' or ''beats-all winner'', is formally called the ''Condorcet winner'' or ''Pairwise Majority Rule Winner'' (PMRW). The head-to-head elections need not be done separately; a voter's choice within any given pair can be determined from the ranking. Some elections may not yield a Condorcet winner because voter preferences may be cyclic—that is, it is possible that every candidate has an opponent that defeats them in a two-candidate contest. The possibility of such cyclic preferences is known as the Condorcet paradox. However, a smallest group of candidates that beat all candidates not in the group, known as the Smith set, always exists. The Smith set is guaranteed to have the Condorcet winner in it should one exist. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |