|
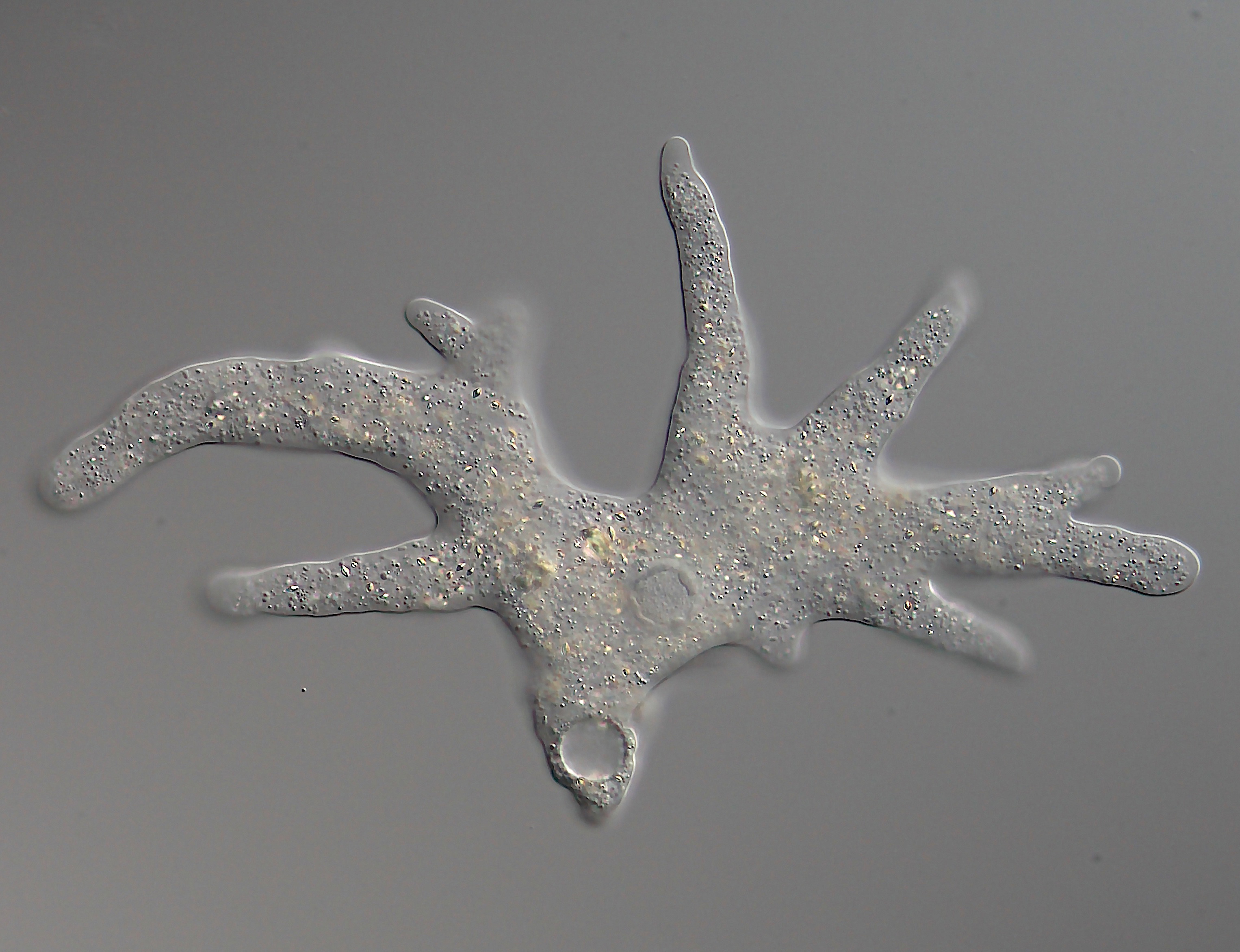
Amoeba Order
In mathematics, the amoeba order is the partial order of open subsets of 2''ω'' of measure less than 1/2, ordered by reverse inclusion. Amoeba forcing is forcing with the amoeba order; it adds a measure 1 set of random reals. There are several variations, where 2''ω'' is replaced by the real numbers or a real vector space or the unit interval, and the number 1/2 is replaced by some positive number ''ε''. The name "amoeba order" come from the fact that a subset in the amoeba order can "engulf" a measure zero set by extending a "pseudopod" to form a larger subset in the order containing this measure zero set, which is analogous to the way an amoeba eats food. The amoeba order satisfies the countable chain condition In order theory, a partially ordered set ''X'' is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in ''X'' is countable. Overview There are really two conditions: the ''upwards'' and ''downwards'' countable .... Refere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Order
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''inco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Forcing (mathematics)
In the mathematical discipline of set theory, forcing is a technique for proving consistency and independence results. It was first used by Paul Cohen in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory. Forcing has been considerably reworked and simplified in the following years, and has since served as a powerful technique, both in set theory and in areas of mathematical logic such as recursion theory. Descriptive set theory uses the notions of forcing from both recursion theory and set theory. Forcing has also been used in model theory, but it is common in model theory to define genericity directly without mention of forcing. Intuition Intuitively, forcing consists of expanding the set theoretical universe V to a larger universe V^ . In this bigger universe, for example, one might have many new real numbers, identified with subsets of the set \mathbb of natural numbers, that were not there in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudopod
A pseudopod or pseudopodium (plural: pseudopods or pseudopodia) is a temporary arm-like projection of a eukaryotic cell membrane that is emerged in the direction of movement. Filled with cytoplasm, pseudopodia primarily consist of actin filaments and may also contain microtubules and intermediate filaments. Pseudopods are used for motility and ingestion. They are often found in amoebas. Different types of pseudopodia can be classified by their distinct appearances. Lamellipodia are broad and thin. Filopodia are slender, thread-like, and are supported largely by microfilaments. Lobopodia are bulbous and amoebic. Reticulopodia are complex structures bearing individual pseudopodia which form irregular nets. Axopodia are the phagocytosis type with long, thin pseudopods supported by complex microtubule arrays enveloped with cytoplasm; they respond rapidly to physical contact. Some pseudopodial cells are able to use multiple types of pseudopodia depending on the situation: Most of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amoeba
An amoeba (; less commonly spelled ameba or amœba; plural ''am(o)ebas'' or ''am(o)ebae'' ), often called an amoeboid, is a type of cell or unicellular organism with the ability to alter its shape, primarily by extending and retracting pseudopods. Amoebae do not form a single taxonomic group; instead, they are found in every major lineage of eukaryotic organisms. Amoeboid cells occur not only among the protozoa, but also in fungi, algae, and animals. Microbiologists often use the terms "amoeboid" and "amoeba" interchangeably for any organism that exhibits amoeboid movement. In older classification systems, most amoebae were placed in the class or subphylum Sarcodina, a grouping of single-celled organisms that possess pseudopods or move by protoplasmic flow. However, molecular phylogenetic studies have shown that Sarcodina is not a monophyletic group whose members share common descent. Consequently, amoeboid organisms are no longer classified together in one group.Jan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Countable Chain Condition
In order theory, a partially ordered set ''X'' is said to satisfy the countable chain condition, or to be ccc, if every strong antichain in ''X'' is countable. Overview There are really two conditions: the ''upwards'' and ''downwards'' countable chain conditions. These are not equivalent. The countable chain condition means the downwards countable chain condition, in other words no two elements have a common lower bound. This is called the "countable chain condition" rather than the more logical term "countable antichain condition" for historical reasons related to certain chains of open sets in topological spaces and chains in complete Boolean algebras, where chain conditions sometimes happen to be equivalent to antichain conditions. For example, if κ is a cardinal, then in a complete Boolean algebra every antichain has size less than κ if and only if there is no descending κ-sequence of elements, so chain conditions are equivalent to antichain conditions. Partial orders and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual differe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |