|
Absolute Generality
In philosophical logic Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophic ..., metaphysics, and the philosophy of language, the problem of absolute generality is the problem of referring to absolutely everything. Historically, philosophers have assumed that some of their statements are absolutely general, referring to truly everything. In recent years, logicians working in the logic of Quantifier (logic), quantification and logical paradox, paradox have challenged this view, arguing that it is impossible for the logical quantifiers to range over an absolutely unrestricted domain. Philosophers who deny the possibility of absolutely unrestricted quantification (often called ''generality relativists'') argue that attempting to speak absolutely generally generates paradoxes such as Russell's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Philosophical Logic
Understood in a narrow sense, philosophical logic is the area of logic that studies the application of logical methods to philosophical problems, often in the form of extended logical systems like modal logic. Some theorists conceive philosophical logic in a wider sense as the study of the scope and nature of logic in general. In this sense, philosophical logic can be seen as identical to the philosophy of logic, which includes additional topics like how to define logic or a discussion of the fundamental concepts of logic. The current article treats philosophical logic in the narrow sense, in which it forms one field of inquiry within the philosophy of logic. An important issue for philosophical logic is the question of how to classify the great variety of non-classical logical systems, many of which are of rather recent origin. One form of classification often found in the literature is to distinguish between extended logics and deviant logics. Logic itself can be defined as t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Metaphysics
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of human understanding. Some philosophers, including Aristotle, designate metaphysics as first philosophy to suggest that it is more fundamental than other forms of philosophical inquiry. Metaphysics encompasses a wide range of general and abstract topics. It investigates the nature of existence, the features all entities have in common, and their division into categories of being. An influential division is between particulars and universals. Particulars are individual unique entities, like a specific apple. Universals are general features that different particulars have in common, like the color . Modal metaphysics examines what it means for something to be possible or necessary. Metaphysicians also explore the concepts of space, time, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Philosophy Of Language
Philosophy of language refers to the philosophical study of the nature of language. It investigates the relationship between language, language users, and the world. Investigations may include inquiry into the nature of Meaning (philosophy), meaning, intentionality, reference, the constitution of sentences, concepts, learning, and thought. Gottlob Frege and Bertrand Russell were pivotal figures in analytic philosophy's "linguistic turn". These writers were followed by Ludwig Wittgenstein (''Tractatus Logico-Philosophicus''), the Vienna Circle, Logical positivism, logical positivists, and Willard Van Orman Quine. History Ancient philosophy In the West, inquiry into language stretches back to the 5th century BC with philosophers such as Socrates, Plato, Aristotle, and the Stoics. Linguistic speculation predated systematic descriptions of grammar which emerged in India and in Greece. In the dialogue ''Cratylus (dialogue), Cratylus'', Plato considered the question of whether ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Quantifier (logic)
In logic, a quantifier is an operator that specifies how many individuals in the domain of discourse satisfy an open formula. For instance, the universal quantifier \forall in the first-order formula \forall x P(x) expresses that everything in the domain satisfies the property denoted by P. On the other hand, the existential quantifier \exists in the formula \exists x P(x) expresses that there exists something in the domain which satisfies that property. A formula where a quantifier takes widest scope is called a quantified formula. A quantified formula must contain a bound variable and a subformula specifying a property of the referent of that variable. The most commonly used quantifiers are \forall and \exists. These quantifiers are standardly defined as duals; in classical logic: each can be defined in terms of the other using negation. They can also be used to define more complex quantifiers, as in the formula \neg \exists x P(x) which expresses that nothing has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Logical Paradox
A paradox is a logically self-contradictory statement or a statement that runs contrary to one's expectation. It is a statement that, despite apparently valid reasoning from true or apparently true premises, leads to a seemingly self-contradictory or a logically unacceptable conclusion. A paradox usually involves contradictory-yet-interrelated elements that exist simultaneously and persist over time. They result in "persistent contradiction between interdependent elements" leading to a lasting "unity of opposites". In logic, many paradoxes exist that are known to be invalid arguments, yet are nevertheless valuable in promoting critical thinking, while other paradoxes have revealed errors in definitions that were assumed to be rigorous, and have caused axioms of mathematics and logic to be re-examined. One example is Russell's paradox, which questions whether a "list of all lists that do not contain themselves" would include itself and showed that attempts to found set theory on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Russell's Paradox
In mathematical logic, Russell's paradox (also known as Russell's antinomy) is a set-theoretic paradox published by the British philosopher and mathematician, Bertrand Russell, in 1901. Russell's paradox shows that every set theory that contains an unrestricted comprehension principle leads to contradictions. According to the unrestricted comprehension principle, for any sufficiently well-defined property, there is the set of all and only the objects that have that property. Let ''R'' be the set of all sets that are not members of themselves. (This set is sometimes called "the Russell set".) If ''R'' is not a member of itself, then its definition entails that it is a member of itself; yet, if it is a member of itself, then it is not a member of itself, since it is the set of all sets that are not members of themselves. The resulting contradiction is Russell's paradox. In symbols: : Let R = \. Then R \in R \iff R \not \in R. Russell also showed that a version of the paradox co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Löwenheim–Skolem Theorem
In mathematical logic, the Löwenheim–Skolem theorem is a theorem on the existence and cardinality of models, named after Leopold Löwenheim and Thoralf Skolem. The precise formulation is given below. It implies that if a countable first-order theory has an infinite model, then for every infinite cardinal number ''κ'' it has a model of size ''κ'', and that no first-order theory with an infinite model can have a unique model up to isomorphism. As a consequence, first-order theories are unable to control the cardinality of their infinite models. The (downward) Löwenheim–Skolem theorem is one of the two key properties, along with the compactness theorem, that are used in Lindström's theorem to characterize first-order logic. In general, the Löwenheim–Skolem theorem does not hold in stronger logics such as second-order logic. Theorem In its general form, the Löwenheim–Skolem Theorem states that for every signature ''σ'', every infinite ''σ''-structure ''M'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Timothy Williamson
Timothy Williamson (born 6 August 1955) is a British philosopher whose main research interests are in philosophical logic, philosophy of language, epistemology and metaphysics. He is the former Wykeham Professor of Logic at the University of Oxford, and a fellow of New College, Oxford. Education and career Born on 6 August 1955, Williamson's education began at Leighton Park School and continued at Henley Grammar School (now the Henley College). He then went to Balliol College, Oxford University. He graduated in 1976 with a Bachelor of Arts degree with first-class honours in mathematics and philosophy, and in 1980 with a doctorate in philosophy (DPhil) for a thesis entitled ''The Concept of Approximation to the Truth''. Williamson was Professor of Logic and Metaphysics at the University of Edinburgh (1995–2000), fellow and lecturer in philosophy at University College, Oxford (1988–1994), and lecturer in philosophy at Trinity College, Dublin (1980–1988). He took up the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Domain Of Discourse
In the formal sciences, the domain of discourse or universe of discourse (borrowing from the mathematical concept of ''universe'') is the set of entities over which certain variables of interest in some formal treatment may range. It is also defined as the collection of objects being discussed in a specific discourse. In model-theoretical semantics, a universe of discourse is the set of entities that a model is based on. The domain of discourse is usually identified in the preliminaries, so that there is no need in the further treatment to specify each time the range of the relevant variables. Many logicians distinguish, sometimes only tacitly, between the ''domain of a science'' and the ''universe of discourse of a formalization of the science''. Etymology The concept ''universe of discourse'' was used for the first time by George Boole (1854) on page 42 of his '' Laws of Thought'': The concept, probably discovered independently by Boole in 1847, played a crucial role i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
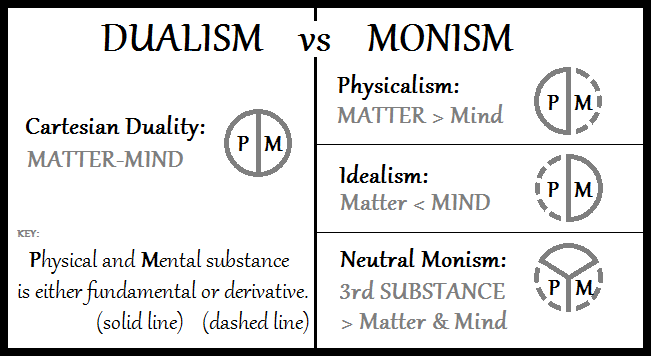 |
Metametaphysics
Metaphysics is the branch of philosophy that examines the basic structure of reality. It is traditionally seen as the study of mind-independent features of the world, but some theorists view it as an inquiry into the conceptual framework of human understanding. Some philosophers, including Aristotle, designate metaphysics as first philosophy to suggest that it is more fundamental than other forms of philosophical inquiry. Metaphysics encompasses a wide range of general and abstract topics. It investigates the nature of existence, the features all entities have in common, and their division into categories of being. An influential division is between particulars and universals. Particulars are individual unique entities, like a specific apple. Universals are general features that different particulars have in common, like the color . Modal metaphysics examines what it means for something to be possible or necessary. Metaphysicians also explore the concepts of space, time, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |