|
ANOVA On Ranks
In statistics, one purpose for the analysis of variance (ANOVA) is to analyze differences in means between groups. The test statistic, ''F'', assumes independence of observations, homogeneous variances, and population normality. ANOVA on ranks is a statistic designed for situations when the normality assumption has been violated. Logic of the ''F'' test on means The ''F'' statistic is a ratio of a numerator to a denominator. Consider randomly selected subjects that are subsequently randomly assigned to groups A, B, and C. Under the truth of the null hypothesis, the variability (or sum of squares) of scores on some dependent variable will be the same within each group. When divided by the degrees of freedom (i.e., based on the number of subjects per group), the denominator of the ''F'' ratio is obtained. Treat the mean for each group as a score, and compute the variability (again, the sum of squares) of those three scores. When divided by its degrees of freedom (i.e., based on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analysis Of Variance
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independence (probability Theory)
Independence is a fundamental notion in probability theory, as in statistics and the theory of stochastic processes. Two events are independent, statistically independent, or stochastically independent if, informally speaking, the occurrence of one does not affect the probability of occurrence of the other or, equivalently, does not affect the odds. Similarly, two random variables are independent if the realization of one does not affect the probability distribution of the other. When dealing with collections of more than two events, two notions of independence need to be distinguished. The events are called pairwise independent if any two events in the collection are independent of each other, while mutual independence (or collective independence) of events means, informally speaking, that each event is independent of any combination of other events in the collection. A similar notion exists for collections of random variables. Mutual independence implies pairwise independe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
In scientific research, the null hypothesis (often denoted ''H''0) is the claim that no difference or relationship exists between two sets of data or variables being analyzed. The null hypothesis is that any experimentally observed difference is due to chance alone, and an underlying causative relationship does not exist, hence the term "null". In addition to the null hypothesis, an alternative hypothesis is also developed, which claims that a relationship does exist between two variables. Basic definitions The ''null hypothesis'' and the ''alternative hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data. The hypotheses are conjectures about a statistical model of the population, which are based on a sample of the population. The tests are core elements of statistical inference, heavily used in the interpretation of scientific experimental data, to separate scientific claims ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wilcoxon Rank-sum
Wilcoxon is a surname, and may refer to: * Charles Wilcoxon, drum educator * Henry Wilcoxon, an actor * Frank Wilcoxon, chemist and statistician, inventor of two non-parametric tests for statistical significance: ** The Wilcoxon signed-rank test The Wilcoxon signed-rank test is a Non-parametric statistics, non-parametric statistical hypothesis testing, statistical hypothesis test used either to test the Location parameter, location of a population based on a sample of data, or to compare ... (also known as the Wilcoxon T test) ** The Wilcoxon rank-sum test (also known as the Mann–Whitney U test). See also * Wilcox (surname) {{surname ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
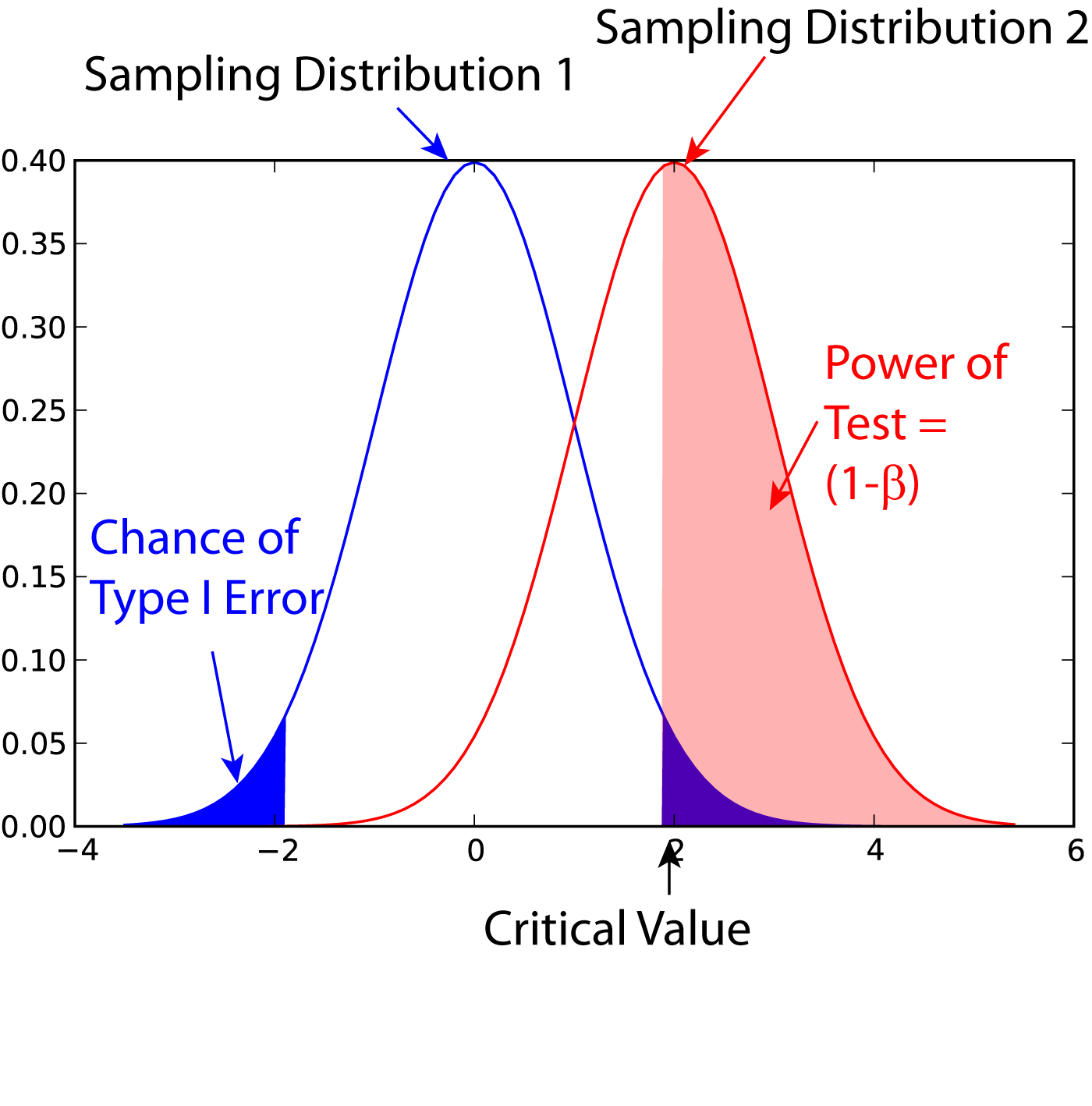
Statistical Power
In statistics, the power of a binary hypothesis test is the probability that the test correctly rejects the null hypothesis (H_0) when a specific alternative hypothesis (H_1) is true. It is commonly denoted by 1-\beta, and represents the chances of a true positive detection conditional on the actual existence of an effect to detect. Statistical power ranges from 0 to 1, and as the power of a test increases, the probability \beta of making a type II error by wrongly failing to reject the null hypothesis decreases. Notation This article uses the following notation: * ''β'' = probability of a Type II error, known as a "false negative" * 1 − ''β'' = probability of a "true positive", i.e., correctly rejecting the null hypothesis. "1 − ''β''" is also known as the power of the test. * ''α'' = probability of a Type I error, known as a "false positive" * 1 − ''α'' = probability of a "true negative", i.e., correctly not rejecting the null hypothesis Description For a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monte Carlo Method
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution. In physics-related problems, Monte Carlo methods are useful for simulating systems with many coupled degrees of freedom, such as fluids, disordered materials, strongly coupled solids, and cellular structures (see cellular Potts model, interacting particle systems, McKean–Vlasov processes, kinetic models of gases). Other examples include modeling phenomena with significant uncertainty in inputs such as the calculation of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
T-test
A ''t''-test is any statistical hypothesis test in which the test statistic follows a Student's ''t''-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known (typically, the scaling term is unknown and therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's ''t'' distribution. The ''t''-test's most common application is to test whether the means of two populations are different. History The term "''t''-statistic" is abbreviated from "hypothesis test statistic". In statistics, the t-distribution was first derived as a posterior distribution in 1876 by Helmert and Lüroth. The t-distribution also appeared in a more general form as Pearson Type IV distribution in Karl Pearson's 1895 paper. However, the T-Distribution, also known as Student's t-distr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hotelling's T-square Distribution
In statistics, particularly in hypothesis testing, the Hotelling's ''T''-squared distribution (''T''2), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the ''F''-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's ''t''-distribution. The Hotelling's ''t''-squared statistic (''t''2) is a generalization of Student's ''t''-statistic that is used in multivariate hypothesis testing. Motivation The distribution arises in multivariate statistics in undertaking tests of the differences between the (multivariate) means of different populations, where tests for univariate problems would make use of a ''t''-test. The distribution is named for Harold Hotelling, who developed it as a generalization of Student's ''t''-distribution. Definition If the vector d is Gaussian multivariate-distributed with zero mean and un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |