capillary action on:
[Wikipedia]
[Google]
[Amazon]
 Capillary action (sometimes called capillarity, capillary motion, capillary rise, capillary effect, or wicking) is the process of a
Capillary action (sometimes called capillarity, capillary motion, capillary rise, capillary effect, or wicking) is the process of a

 Capillary penetration in porous media shares its dynamic mechanism with flow in hollow tubes, as both processes are resisted by viscous forces. Consequently, a common apparatus used to demonstrate the phenomenon is the ''capillary tube''. When the lower end of a glass tube is placed in a liquid, such as water, a concave meniscus forms.
Capillary penetration in porous media shares its dynamic mechanism with flow in hollow tubes, as both processes are resisted by viscous forces. Consequently, a common apparatus used to demonstrate the phenomenon is the ''capillary tube''. When the lower end of a glass tube is placed in a liquid, such as water, a concave meniscus forms.
 In physiology, capillary action is essential for the drainage of continuously produced tear fluid from the eye. Two canaliculi of tiny diameter are present in the inner corner of the eyelid, also called the lacrimal ducts; their openings can be seen with the naked eye within the lacrymal sacs when the eyelids are everted.
Wicking is the absorption of a liquid by a material in the manner of a candle wick.
Paper towels absorb liquid through capillary action, allowing a
In physiology, capillary action is essential for the drainage of continuously produced tear fluid from the eye. Two canaliculi of tiny diameter are present in the inner corner of the eyelid, also called the lacrimal ducts; their openings can be seen with the naked eye within the lacrymal sacs when the eyelids are everted.
Wicking is the absorption of a liquid by a material in the manner of a candle wick.
Paper towels absorb liquid through capillary action, allowing a
 The height ''h'' of a liquid column is given by Jurin's law G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ,
:
where is the liquid-air
The height ''h'' of a liquid column is given by Jurin's law G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ,
:
where is the liquid-air
file:Kapilláris emelkedés 1.jpg
file:Kapilláris emelkedés 2.jpg
file:Kapilláris emelkedés 3.jpg
file:Kapilláris emelkedés 4.jpg
file:Kapilláris emelkedés 5.jpg
file:Kapilláris emelkedés 6.jpg
 When a dry porous medium is brought into contact with a liquid, it will absorb the liquid at a rate which decreases over time. When considering evaporation, liquid penetration will reach a limit dependent on parameters of temperature, humidity and permeability. This process is known as evaporation limited capillary penetration and is widely observed in common situations including fluid absorption into paper and rising damp in concrete or masonry walls. For a bar shaped section of material with cross-sectional area ''A'' that is wetted on one end, the cumulative volume ''V'' of absorbed liquid after a time ''t'' is
:
where ''S'' is the sorptivity of the medium, in units of m·s−1/2 or mm·min−1/2. This time dependence relation is similar to Washburn's equation for the wicking in capillaries and porous media. The quantity
:
is called the cumulative liquid intake, with the dimension of length. The wetted length of the bar, that is the distance between the wetted end of the bar and the so-called ''wet front'', is dependent on the fraction ''f'' of the volume occupied by voids. This number ''f'' is the
When a dry porous medium is brought into contact with a liquid, it will absorb the liquid at a rate which decreases over time. When considering evaporation, liquid penetration will reach a limit dependent on parameters of temperature, humidity and permeability. This process is known as evaporation limited capillary penetration and is widely observed in common situations including fluid absorption into paper and rising damp in concrete or masonry walls. For a bar shaped section of material with cross-sectional area ''A'' that is wetted on one end, the cumulative volume ''V'' of absorbed liquid after a time ''t'' is
:
where ''S'' is the sorptivity of the medium, in units of m·s−1/2 or mm·min−1/2. This time dependence relation is similar to Washburn's equation for the wicking in capillaries and porous media. The quantity
:
is called the cumulative liquid intake, with the dimension of length. The wetted length of the bar, that is the distance between the wetted end of the bar and the so-called ''wet front'', is dependent on the fraction ''f'' of the volume occupied by voids. This number ''f'' is the
page 131 on Google books
The above description is for the case where gravity and evaporation do not play a role. Sorptivity is a relevant property of building materials, because it affects the amount of rising dampness. Some values for the sorptivity of building materials are in the table below.
 Capillary action (sometimes called capillarity, capillary motion, capillary rise, capillary effect, or wicking) is the process of a
Capillary action (sometimes called capillarity, capillary motion, capillary rise, capillary effect, or wicking) is the process of a liquid
Liquid is a state of matter with a definite volume but no fixed shape. Liquids adapt to the shape of their container and are nearly incompressible, maintaining their volume even under pressure. The density of a liquid is usually close to th ...
flowing in a narrow space without the assistance of external forces like gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
.
The effect can be seen in the drawing up of liquids between the hairs of a paint-brush, in a thin tube such as a straw
Straw is an agricultural byproduct consisting of the dry wikt:stalk, stalks of cereal plants after the grain and chaff have been removed. It makes up about half of the crop yield, yield by weight of cereal crops such as barley, oats, rice, ry ...
, in porous materials such as paper and plaster, in some non-porous materials such as clay
Clay is a type of fine-grained natural soil material containing clay minerals (hydrous aluminium phyllosilicates, e.g. kaolinite, ). Most pure clay minerals are white or light-coloured, but natural clays show a variety of colours from impuriti ...
and liquefied carbon fiber
Carbon fiber-reinforced polymers (American English), carbon-fibre-reinforced polymers ( Commonwealth English), carbon-fiber-reinforced plastics, carbon-fiber reinforced-thermoplastic (CFRP, CRP, CFRTP), also known as carbon fiber, carbon comp ...
, or in a biological cell.
It occurs because of intermolecular force
An intermolecular force (IMF; also secondary force) is the force that mediates interaction between molecules, including the electromagnetic forces of attraction
or repulsion which act between atoms and other types of neighbouring particles (e.g. ...
s between the liquid and surrounding solid surfaces. If the diameter of the tube is sufficiently small, then the combination of surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
(which is caused by cohesion within the liquid) and adhesive forces between the liquid and container wall act to propel the liquid.
Etymology
Capillary comes from the Latin word capillaris, meaning "of or resembling hair". The meaning stems from the tiny, hairlike diameter of a capillary.History
The first recorded observation of capillary action was byLeonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested o ...
. A former student of Galileo
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642), commonly referred to as Galileo Galilei ( , , ) or mononymously as Galileo, was an Italian astronomer, physicist and engineer, sometimes described as a poly ...
, Niccolò Aggiunti, was said to have investigated capillary action. In 1660, capillary action was still a novelty to the Irish chemist Robert Boyle, when he reported that "some inquisitive French Men" had observed that when a capillary tube was dipped into water, the water would ascend to "some height in the Pipe". Boyle then reported an experiment in which he dipped a capillary tube into red wine and then subjected the tube to a partial vacuum. He found that the vacuum had no observable influence on the height of the liquid in the capillary, so the behavior of liquids in capillary tubes was due to some phenomenon different from that which governed mercury barometers.
Others soon followed Boyle's lead. Some (e.g., Honoré Fabri, Jacob Bernoulli
Jacob Bernoulli (also known as James in English or Jacques in French; – 16 August 1705) was a Swiss mathematician. He sided with Gottfried Wilhelm Leibniz during the Leibniz–Newton calculus controversy and was an early proponent of Leibniz ...
) thought that liquids rose in capillaries because air could not enter capillaries as easily as liquids, so the air pressure was lower inside capillaries. Others (e.g., Isaac Vossius, Giovanni Alfonso Borelli, Louis Carré, Francis Hauksbee, Josia Weitbrecht) thought that the particles of liquid were attracted to each other and to the walls of the capillary.
Although experimental studies continued during the 18th century, a successful quantitative treatment of capillary action was not attained until 1805 by two investigators: Thomas Young of the United Kingdom and Pierre-Simon Laplace
Pierre-Simon, Marquis de Laplace (; ; 23 March 1749 – 5 March 1827) was a French polymath, a scholar whose work has been instrumental in the fields of physics, astronomy, mathematics, engineering, statistics, and philosophy. He summariz ...
of France. They derived the Young–Laplace equation of capillary action. By 1830, the German mathematician Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; ; ; 30 April 177723 February 1855) was a German mathematician, astronomer, geodesist, and physicist, who contributed to many fields in mathematics and science. He was director of the Göttingen Observatory and ...
had determined the boundary conditions governing capillary action (i.e., the conditions at the liquid-solid interface). In 1871, the British physicist Sir William Thomson (later Lord Kelvin) determined the effect of the meniscus on a liquid's vapor pressure
Vapor pressure or equilibrium vapor pressure is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system. The equilibrium vapor pressure is an indicat ...
—a relation known as the Kelvin equation
The kelvin (symbol: K) is the SI base unit, base unit for temperature in the International System of Units (SI). The Kelvin scale is an absolute scale, absolute temperature scale that starts at the lowest possible temperature (absolute zero), ...
. German physicist Franz Ernst Neumann (1798–1895) subsequently determined the interaction between two immiscible liquids.
Albert Einstein
Albert Einstein (14 March 187918 April 1955) was a German-born theoretical physicist who is best known for developing the theory of relativity. Einstein also made important contributions to quantum mechanics. His mass–energy equivalence f ...
's first paper, which was submitted to '' Annalen der Physik'' in 1900, was on capillarity.
Phenomena and physics

 Capillary penetration in porous media shares its dynamic mechanism with flow in hollow tubes, as both processes are resisted by viscous forces. Consequently, a common apparatus used to demonstrate the phenomenon is the ''capillary tube''. When the lower end of a glass tube is placed in a liquid, such as water, a concave meniscus forms.
Capillary penetration in porous media shares its dynamic mechanism with flow in hollow tubes, as both processes are resisted by viscous forces. Consequently, a common apparatus used to demonstrate the phenomenon is the ''capillary tube''. When the lower end of a glass tube is placed in a liquid, such as water, a concave meniscus forms. Adhesion
Adhesion is the tendency of dissimilar particles or interface (matter), surfaces to cling to one another. (Cohesion (chemistry), Cohesion refers to the tendency of similar or identical particles and surfaces to cling to one another.)
The ...
occurs between the fluid and the solid inner wall pulling the liquid column along until there is a sufficient mass of liquid for gravitational forces to overcome these intermolecular forces. The contact length (around the edge) between the top of the liquid column and the tube is proportional to the radius of the tube, while the weight of the liquid column is proportional to the square of the tube's radius. So, a narrow tube will draw a liquid column along further than a wider tube will, given that the inner water molecules cohere sufficiently to the outer ones.
Examples
In the built environment, evaporation limited capillary penetration is responsible for the phenomenon of rising damp inconcrete
Concrete is a composite material composed of aggregate bound together with a fluid cement that cures to a solid over time. It is the second-most-used substance (after water), the most–widely used building material, and the most-manufactur ...
and masonry
Masonry is the craft of building a structure with brick, stone, or similar material, including mortar plastering which are often laid in, bound, and pasted together by mortar (masonry), mortar. The term ''masonry'' can also refer to the buildin ...
, while in industry and diagnostic medicine this phenomenon is increasingly being harnessed in the field of paper-based microfluidics.
fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
to be transferred from a surface to the towel. The small pores of a sponge
Sponges or sea sponges are primarily marine invertebrates of the animal phylum Porifera (; meaning 'pore bearer'), a basal clade and a sister taxon of the diploblasts. They are sessile filter feeders that are bound to the seabed, and a ...
act as small capillaries, causing it to absorb a large amount of fluid. Some textile fabrics are said to use capillary action to "wick" sweat away from the skin. These are often referred to as wicking fabrics, after the capillary properties of candle
A candle is an ignitable candle wick, wick embedded in wax, or another flammable solid substance such as tallow, that provides light, and in some cases, a Aroma compound, fragrance. A candle can also provide heat or a method of keeping time. ...
and lamp wicks.
Capillary action is observed in thin layer chromatography, in which a solvent moves vertically up a plate via capillary action. In this case the pores are gaps between very small particles.
Capillary action draws ink to the tips of fountain pen nibs from a reservoir or cartridge inside the pen.
With some pairs of materials, such as mercury and glass, the intermolecular force
An intermolecular force (IMF; also secondary force) is the force that mediates interaction between molecules, including the electromagnetic forces of attraction
or repulsion which act between atoms and other types of neighbouring particles (e.g. ...
s within the liquid exceed those between the solid and the liquid, so a convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
meniscus forms and capillary action works in reverse.
In hydrology
Hydrology () is the scientific study of the movement, distribution, and management of water on Earth and other planets, including the water cycle, water resources, and drainage basin sustainability. A practitioner of hydrology is called a hydro ...
, capillary action describes the attraction of water molecules to soil particles. Capillary action is responsible for moving groundwater
Groundwater is the water present beneath Earth's surface in rock and Pore space in soil, soil pore spaces and in the fractures of stratum, rock formations. About 30 percent of all readily available fresh water in the world is groundwater. A unit ...
from wet areas of the soil to dry areas. Differences in soil potential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple r ...
() drive capillary action in soil.
A practical application of capillary action is the capillary action siphon. Instead of utilizing a hollow tube (as in most siphons), this device consists of a length of cord made of a fibrous material (cotton cord or string works well). After saturating the cord with water, one (weighted) end is placed in a reservoir full of water, and the other end placed in a receiving vessel. The reservoir must be higher than the receiving vessel. A related but simplified capillary siphon only consists of two hook-shaped stainless-steel rods, whose surface is hydrophilic, allowing water to wet the narrow grooves between them. Due to capillary action and gravity, water will slowly transfer from the reservoir to the receiving vessel. This simple device can be used to water houseplants when nobody is home. This property is also made use of in the lubrication of steam locomotives: wicks of worsted wool are used to draw oil from reservoirs into delivery pipes leading to the bearings.
In plants and animals
Capillary action is seen in many plants, and plays a part intranspiration
Transpiration is the process of water movement through a plant and its evaporation from aerial parts, such as leaves, stems and flowers. It is a passive process that requires no energy expense by the plant. Transpiration also cools plants, c ...
. Water is brought high up in trees by branching; evaporation at the leaves creating depressurization; probably by osmotic pressure
Osmotic pressure is the minimum pressure which needs to be applied to a Solution (chemistry), solution to prevent the inward flow of its pure solvent across a semipermeable membrane.
It is also defined as the measure of the tendency of a soluti ...
added at the roots; and possibly at other locations inside the plant, especially when gathering humidity with air roots.
Capillary action for uptake of water has been described in some small animals, such as '' Ligia exotica'' and '' Moloch horridus''.
Height of a meniscus
Capillary rise of liquid in a capillary
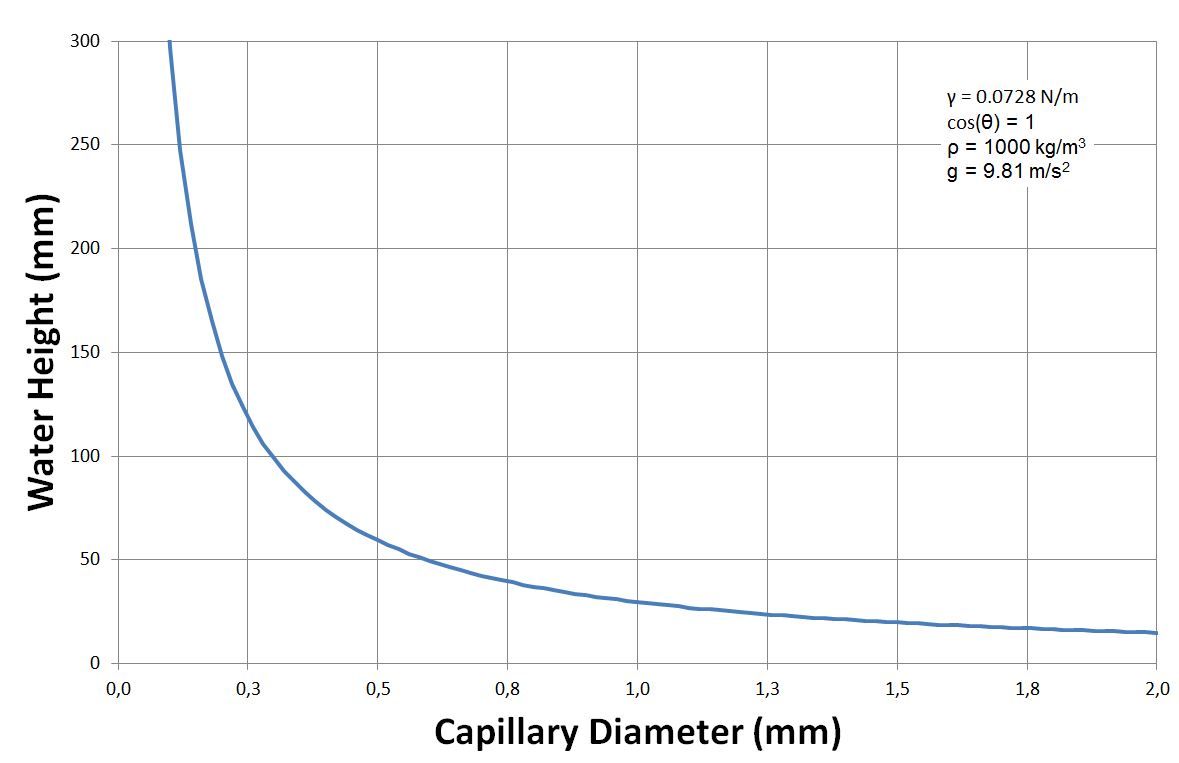
 The height ''h'' of a liquid column is given by Jurin's law G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ,
:
where is the liquid-air
The height ''h'' of a liquid column is given by Jurin's law G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ,
:
where is the liquid-air surface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
(force/unit length), ''θ'' is the contact angle, ''ρ'' is the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
of liquid (mass/volume), ''g'' is the local acceleration due to gravity (length/square of time), and ''r'' is the radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
of tube.
As ''r'' is in the denominator, the thinner the space in which the liquid can travel, the further up it goes. Likewise, lighter liquid and lower gravity increase the height of the column.
For a water-filled glass tube in air at standard laboratory conditions, at 20°C, , and . Because water spreads on clean glass, the effective equilibrium contact angle is approximately zero. For these values, the height of the water column is
:
Thus for a radius glass tube in lab conditions given above, the water would rise an unnoticeable . However, for a radius tube, the water would rise , and for a radius tube, the water would rise .
Capillary rise of liquid between two glass plates
The product of layer thickness (''d'') and elevation height (''h'') is constant (''d''·''h'' = constant), the two quantities are inversely proportional. The surface of the liquid between the planes is hyperbola.Liquid transport in porous media
 When a dry porous medium is brought into contact with a liquid, it will absorb the liquid at a rate which decreases over time. When considering evaporation, liquid penetration will reach a limit dependent on parameters of temperature, humidity and permeability. This process is known as evaporation limited capillary penetration and is widely observed in common situations including fluid absorption into paper and rising damp in concrete or masonry walls. For a bar shaped section of material with cross-sectional area ''A'' that is wetted on one end, the cumulative volume ''V'' of absorbed liquid after a time ''t'' is
:
where ''S'' is the sorptivity of the medium, in units of m·s−1/2 or mm·min−1/2. This time dependence relation is similar to Washburn's equation for the wicking in capillaries and porous media. The quantity
:
is called the cumulative liquid intake, with the dimension of length. The wetted length of the bar, that is the distance between the wetted end of the bar and the so-called ''wet front'', is dependent on the fraction ''f'' of the volume occupied by voids. This number ''f'' is the
When a dry porous medium is brought into contact with a liquid, it will absorb the liquid at a rate which decreases over time. When considering evaporation, liquid penetration will reach a limit dependent on parameters of temperature, humidity and permeability. This process is known as evaporation limited capillary penetration and is widely observed in common situations including fluid absorption into paper and rising damp in concrete or masonry walls. For a bar shaped section of material with cross-sectional area ''A'' that is wetted on one end, the cumulative volume ''V'' of absorbed liquid after a time ''t'' is
:
where ''S'' is the sorptivity of the medium, in units of m·s−1/2 or mm·min−1/2. This time dependence relation is similar to Washburn's equation for the wicking in capillaries and porous media. The quantity
:
is called the cumulative liquid intake, with the dimension of length. The wetted length of the bar, that is the distance between the wetted end of the bar and the so-called ''wet front'', is dependent on the fraction ''f'' of the volume occupied by voids. This number ''f'' is the porosity
Porosity or void fraction is a measure of the void (i.e. "empty") spaces in a material, and is a fraction of the volume of voids over the total volume, between 0 and 1, or as a percentage between 0% and 100%. Strictly speaking, some tests measure ...
of the medium; the wetted length is then
:
Some authors use the quantity ''S/f'' as the sorptivity.C. Hall, W.D. Hoff, Water transport in brick, stone, and concrete. (2002page 131 on Google books
The above description is for the case where gravity and evaporation do not play a role. Sorptivity is a relevant property of building materials, because it affects the amount of rising dampness. Some values for the sorptivity of building materials are in the table below.
See also
* * * * * * * * * * * * * * * * * *References
Further reading
* {{Authority control Fluid dynamics Hydrology Surface science Porous media