Wigner quasi-probability distribution on:
[Wikipedia]
[Google]
[Amazon]
The Wigner quasiprobability distribution (also called the Wigner function or the Wigner–Ville distribution, after
 1. ''W''(''x'', ''p'') is a real-valued function.
2. The ''x'' and ''p'' probability distributions are given by the marginals:
:: If the system can be described by a
1. ''W''(''x'', ''p'') is a real-valued function.
2. The ''x'' and ''p'' probability distributions are given by the marginals:
:: If the system can be described by a
pages 86–89
Als
online
). This non-local feature of Moyal time evolution is illustrated in the gallery below, for Hamiltonians more complex than the harmonic oscillator. In the classical limit, the trajectory nature of the time evolution of Wigner functions becomes more and more distinct. At ''ħ'' = 0, the characteristics' trajectories reduce to the classical trajectories of particles in phase space.
 * In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracing and the full wave analysis of the system. Here is replaced with in the small-angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position and angle while still including the effects of interference. If it becomes negative at any point, then simple ray tracing will not suffice to model the system. That is to say, negative values of this function are a symptom of the
* In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracing and the full wave analysis of the system. Here is replaced with in the small-angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position and angle while still including the effects of interference. If it becomes negative at any point, then simple ray tracing will not suffice to model the system. That is to say, negative values of this function are a symptom of the
"Maverick Mathematician: The Life and Science of J. E. Moyal"
ANU E-press, 2006, .
wigner
Wigner function implementation in QuTiP.
Quantum Optics Gallery
Sonogram Visible Speech
GPL-licensed freeware for the Wigner quasiprobability distribution of signal files. {{DEFAULTSORT:Wigner Quasi-Probability Distribution Continuous distributions Concepts in physics Mathematical physics Exotic probabilities Articles containing video clips Quantum optics
Eugene Wigner
Eugene Paul "E. P." Wigner ( hu, Wigner Jenő Pál, ; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his co ...
and Jean-André Ville) is a quasiprobability distribution
A quasiprobability distribution is a mathematical object similar to a probability distribution but which relaxes some of Kolmogorov's axioms of probability theory. Quasiprobabilities share several of general features with ordinary probabilities ...
. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements ...
that appears in Schrödinger's equation to a probability distribution in phase space.
It is a generating function for all spatial autocorrelation functions of a given quantum-mechanical wavefunction .
Thus, it maps on the quantum density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
in the map between real phase-space functions and Hermitian {{Short description, none
Numerous things are named after the French mathematician Charles Hermite (1822–1901):
Hermite
* Cubic Hermite spline, a type of third-degree spline
* Gauss–Hermite quadrature, an extension of Gaussian quadrature m ...
operators introduced by Hermann Weyl in 1927, in a context related to representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by ''representing'' their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essen ...
in mathematics (see Weyl quantization). In effect, it is the Wigner–Weyl transform
In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform (after Hermann Weyl and Eugene Wigner) is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödin ...
of the density matrix, so the realization of that operator in phase space. It was later rederived by Jean Ville in 1948 as a quadratic (in signal) representation of the local time-frequency energy of a signal, effectively a spectrogram
A spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
When applied to an audio signal, spectrograms are sometimes called sonographs, voiceprints, or voicegrams. When the data are represen ...
.
In 1949, José Enrique Moyal
José Enrique Moyal ( he, יוסף הנרי מויאל; 1 October 1910 – 22 May 1998) was an Australian mathematician and mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among ot ...
, who had derived it independently, recognized it as the quantum moment-generating functional, and thus as the basis of an elegant encoding of all quantum expectation values, and hence quantum mechanics, in phase space (see Phase-space formulation
The phase-space formulation of quantum mechanics places the position ''and'' momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position ''or'' momentum representations (see also position and mo ...
). It has applications in statistical mechanics, quantum chemistry, quantum optics
Quantum optics is a branch of atomic, molecular, and optical physics dealing with how individual quanta of light, known as photons, interact with atoms and molecules. It includes the study of the particle-like properties of photons. Photons have ...
, classical optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultrav ...
and signal analysis in diverse fields, such as electrical engineering, seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other ...
, time–frequency analysis for music signals, spectrogram
A spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
When applied to an audio signal, spectrograms are sometimes called sonographs, voiceprints, or voicegrams. When the data are represen ...
s in biology
Biology is the scientific study of life. It is a natural science with a broad scope but has several unifying themes that tie it together as a single, coherent field. For instance, all organisms are made up of cells that process hereditary i ...
and speech processing, and engine design.
Relation to classical mechanics
A classical particle has a definite position and momentum, and hence it is represented by a point in phase space. Given a collection (ensemble
Ensemble may refer to:
Art
* Architectural ensemble
* Ensemble (album), ''Ensemble'' (album), Kendji Girac 2015 album
* Ensemble (band), a project of Olivier Alary
* Ensemble cast (drama, comedy)
* Ensemble (musical theatre), also known as the ...
) of particles, the probability of finding a particle at a certain position in phase space is specified by a probability distribution, the Liouville density. This strict interpretation fails
for a quantum particle, due to the uncertainty principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
. Instead, the above quasiprobability Wigner distribution plays an analogous role, but does not satisfy all the properties of a conventional probability distribution; and, conversely, satisfies boundedness properties unavailable to classical distributions.
For instance, the Wigner distribution can and normally does take on negative values for states which have no classical model—and is a convenient indicator of quantum-mechanical interference. (See below for a characterization of pure states whose Wigner functions are non-negative.)
Smoothing the Wigner distribution through a filter of size larger than (e.g., convolving with a
phase-space Gaussian, a Weierstrass transform
In mathematics, the Weierstrass transform of a function , named after Karl Weierstrass, is a "smoothed" version of obtained by averaging the values of , weighted with a Gaussian centered at ''x''.
Specifically, it is the function define ...
, to yield the Husimi representation, below), results in a positive-semidefinite function, i.e., it may be thought to have been coarsened to a semi-classical one.
Regions of such negative value are provable (by convolving them with a small Gaussian) to be "small": they cannot extend to compact regions larger than a few , and hence disappear in the classical limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict n ...
. They are shielded by the uncertainty principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
, which does not allow precise location within phase-space regions smaller than , and thus renders such " negative probabilities" less paradoxical.
Definition and meaning
The Wigner distribution of a pure state is defined as where is the wavefunction, and and are position and momentum, but could be any conjugate variable pair (e.g. real and imaginary parts of the electric field or frequency and time of a signal). Note that it may have support in even in regions where has no support in ("beats"). It is symmetric in and : : where is the normalized momentum-space wave function, proportional to the Fourier transform of . In 3D, : In the general case, which includes mixed states, it is the Wigner transform of thedensity matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
:
:
where ⟨''x'', ''ψ''⟩ = . This Wigner transformation (or map) is the inverse of the Weyl transform, which maps phase-space functions to Hilbert-space operators, in Weyl quantization.
Thus, the Wigner function is the cornerstone of quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistr ...
in phase space.
In 1949, José Enrique Moyal
José Enrique Moyal ( he, יוסף הנרי מויאל; 1 October 1910 – 22 May 1998) was an Australian mathematician and mathematical physicist who contributed to aeronautical engineering, electrical engineering and statistics, among ot ...
elucidated how the Wigner function provides the integration measure (analogous to a probability density function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) ca ...
) in phase space, to yield expectation values from phase-space c-number
The term Number C (or C number) is an old nomenclature used by Paul Dirac which refers to real and complex numbers. It is used to distinguish from operators (q-numbers or quantum numbers) in quantum mechanics.
Although c-numbers are commuting, th ...
functions uniquely associated to suitably ordered operators through Weyl's transform (see Wigner–Weyl transform
In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform (after Hermann Weyl and Eugene Wigner) is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödin ...
and property 7 below), in a manner evocative of classical probability theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set ...
.
Specifically, an operator's expectation value is a "phase-space average" of the Wigner transform of that operator:
:
Mathematical properties
 1. ''W''(''x'', ''p'') is a real-valued function.
2. The ''x'' and ''p'' probability distributions are given by the marginals:
:: If the system can be described by a
1. ''W''(''x'', ''p'') is a real-valued function.
2. The ''x'' and ''p'' probability distributions are given by the marginals:
:: If the system can be described by a pure state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in t ...
, one gets
:: If the system can be described by a pure state
In quantum physics, a quantum state is a mathematical entity that provides a probability distribution for the outcomes of each possible measurement on a system. Knowledge of the quantum state together with the rules for the system's evolution in t ...
, one has
::
: Typically the trace of the density matrix '''' is equal to 1.
3. ''W''(''x'', ''p'') has the following reflection symmetries:
:* Time symmetry:
:* Space symmetry:
4. ''W''(''x'', ''p'') is Galilei-covariant:
::
: It is not Lorentz-covariant
In relativistic physics, Lorentz symmetry or Lorentz invariance, named after the Dutch physicist Hendrik Lorentz, is an equivalence of observation or observational symmetry due to special relativity implying that the laws of physics stay the same ...
.
5. The equation of motion for each point in the phase space is classical in the absence of forces:
::
: In fact, it is classical even in the presence of harmonic forces.
6. State overlap is calculated as
::
7. Operator expectation values (averages) are calculated as phase-space averages of the respective Wigner transforms:
::
::
8. For ''W''(''x'', ''p'') to represent physical (positive) density matrices, it must satisfy
::
: for all pure states , θ⟩.
9. By virtue of the Cauchy–Schwarz inequality, for a pure state, it is constrained to be bounded:
::
: This bound disappears in the classical limit, ''ħ'' → 0. In this limit, ''W''(''x'', ''p'') reduces to the probability density in coordinate space ''x'', usually highly localized, multiplied by δ-functions in momentum: the classical limit is "spiky". Thus, this quantum-mechanical bound precludes a Wigner function which is a perfectly localized δ-function in phase space, as a reflection of the uncertainty principle.
10. The Wigner transformation is simply the Fourier transform of the antidiagonal
In linear algebra, the main diagonal (sometimes principal diagonal, primary diagonal, leading diagonal, major diagonal, or good diagonal) of a matrix A is the list of entries a_ where i = j. All off-diagonal elements are zero in a diagonal matrix. ...
s of the density matrix, when that matrix is expressed in a position basis.
Examples
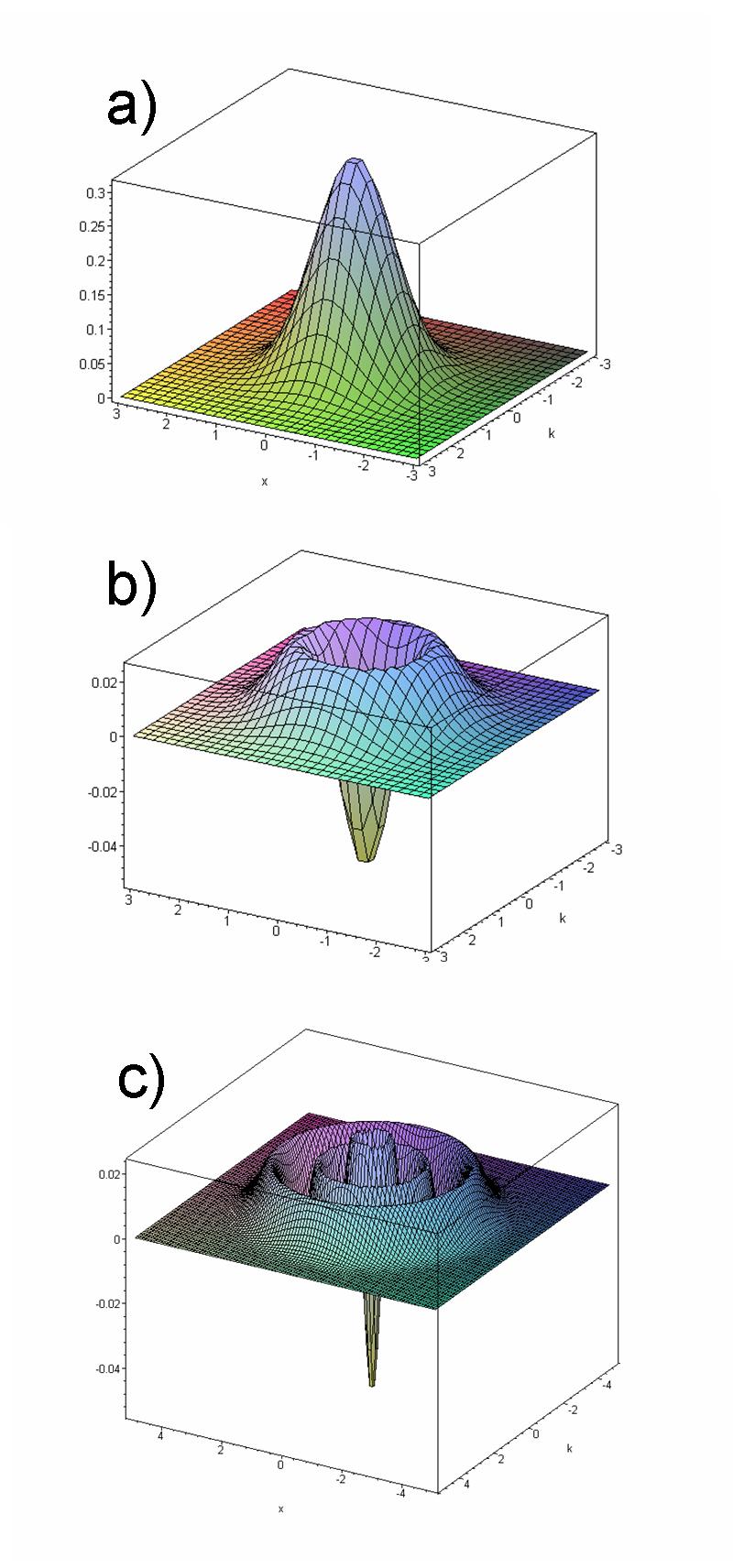
Let be the -thFock state
In quantum mechanics, a Fock state or number state is a quantum state that is an element of a Fock space with a well-defined number of particles (or quanta). These states are named after the Soviet physicist Vladimir Fock. Fock states play an im ...
of a quantum harmonic oscillator. Groenewold (1946) discovered its associated Wigner function, in dimensionless variables:
:
where denotes the -th Laguerre polynomial In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834–1886), are solutions of Laguerre's equation:
xy'' + (1 - x)y' + ny = 0
which is a second-order linear differential equation. This equation has nonsingular solutions only ...
.
This may follow from the expression for the static eigenstate wavefunctions,
:
where is the -th Hermite polynomial
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
* signal processing as Hermitian wavelets for wavelet transform analysis
* probability, such as the Edgeworth series, as well as ...
. From the above definition of the Wigner function, upon a change of integration variables,
:
The expression then follows from the integral relation between Hermite and Laguerre polynomials.
Evolution equation for Wigner function
The Wigner transformation is a general invertible transformation of an operator on a Hilbert space to a function ''g''(''x'', ''p'') on phase space and is given by : Hermitian operators map to real functions. The inverse of this transformation, from phase space to Hilbert space, is called the Weyl transformation: : (not to be confused with the distinct Weyl transformation in differential geometry). The Wigner function discussed here is thus seen to be the Wigner transform of thedensity matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
operator ''ρ̂''. Thus the trace of an operator with the density matrix Wigner-transforms to the equivalent phase-space integral overlap of with the Wigner function.
The Wigner transform of the von Neumann evolution equation of the density matrix in the Schrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators (observables and others) are mostly constant with respect to time (an exception is the Hamiltonian which may ...
is Moyal's evolution equation for the Wigner function:
where is the Hamiltonian, and Liouville equation
:''For Liouville's equation in dynamical systems, see Liouville's theorem (Hamiltonian).''
: ''For Liouville's equation in quantum mechanics, see Von Neumann equation.''
: ''For Liouville's equation in Euclidean space, see Liouville–Bratu–Gel ...
of classical statistical mechanics.
Formally, the classical Liouville equation can be solved in terms of the phase-space particle trajectories which are solutions of the classical Hamilton equations. This technique of solving partial differential equations is known as the method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial ...
. This method transfers to quantum systems, where the characteristics' "trajectories" now determine the evolution of Wigner functions. The solution of the Moyal evolution equation for the Wigner function is represented formally as
:
where and are the characteristic trajectories subject to the quantum Hamilton equations with initial conditions and , and where -product composition is understood for all argument functions.
Since -composition of functions is ''thoroughly nonlocal'' (the "quantum probability fluid" diffuses, as observed by Moyal), vestiges of local trajectories in quantum systems are barely discernible in the evolution of the Wigner distribution function. In the integral representation of -products, successive operations by them have been adapted to a phase-space path integral, to solve the evolution equation for the Wigner function (see also B. Segev: ''Evolution kernels for phase space distributions''. In: See especially section 5. "Path integral for the propagator" opages 86–89
Als
online
). This non-local feature of Moyal time evolution is illustrated in the gallery below, for Hamiltonians more complex than the harmonic oscillator. In the classical limit, the trajectory nature of the time evolution of Wigner functions becomes more and more distinct. At ''ħ'' = 0, the characteristics' trajectories reduce to the classical trajectories of particles in phase space.
Harmonic-oscillator time evolution
In the special case of the quantum harmonic oscillator, however, the evolution is simple and appears identical to the classical motion: a rigid rotation in phase space with a frequency given by the oscillator frequency. This is illustrated in the gallery below. This same time evolution occurs with quantum states of light modes, which are harmonic oscillators.Classical limit
The Wigner function allows one to study theclassical limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict n ...
, offering a comparison of the classical and quantum dynamics in phase space.
It has been suggested that the Wigner function approach can be viewed as a quantum analogy to the operatorial formulation of classical mechanics introduced in 1932 by Bernard Koopman
Bernard Osgood Koopman (January 19, 1900 – August 18, 1981) was a French-born American mathematician, known for his work in ergodic theory, the foundations of probability, statistical theory and operations research.
Education and work
Af ...
and John von Neumann
John von Neumann (; hu, Neumann János Lajos, ; December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. He was regarded as having perhaps the widest cove ...
: the time evolution of the Wigner function approaches, in the limit ''ħ'' → 0, the time evolution of the Koopman–von Neumann wavefunction of a classical particle.
Positivity of the Wigner function
As already noted, the Wigner function of quantum state typically takes some negative values. Indeed, for a pure state in one variable, if for all and , then the wave function must have the form : for some complex numbers with (Hudson's theorem). Note that is allowed to be complex, so that is not necessarily a Gaussian wave packet in the usual sense. Thus, pure states with non-negative Wigner functions are not necessarily minimum-uncertainty states in the sense of the Heisenberg uncertainty formula; rather, they give equality in the Schrödinger uncertainty formula, which includes an anticommutator term in addition to the commutator term. (With careful definition of the respective variances, all pure-state Wigner functions lead to Heisenberg's inequality all the same.) In higher dimensions, the characterization of pure states with non-negative Wigner functions is similar; the wave function must have the form : where is a symmetric complex matrix whose real part is positive-definite, is a complex vector, and is a complex number.F. Soto and P. Claverie, "When is the Wigner function of multidimensional systems nonnegative?", ''Journal of Mathematical Physics'' 24 (1983) 97–100. The Wigner function of any such state is a Gaussian distribution on phase space. Soto and Claverie give an elegant proof of this characterization, using the Segal–Bargmann transform. The reasoning is as follows. The Husimi Q function of may be computed as the squared magnitude of the Segal–Bargmann transform of , multiplied by a Gaussian. Meanwhile, the Husimi Q function is the convolution of the Wigner function with a Gaussian. If the Wigner function of is non-negative everywhere on phase space, then the Husimi Q function will be strictly positive everywhere on phase space. Thus, the Segal–Bargmann transform of will be nowhere zero. Thus, by a standard result from complex analysis, we have : for some holomorphic function . But in order for to belong to theSegal–Bargmann space
In mathematics, the Segal–Bargmann space (for Irving Segal and Valentine Bargmann), also known as the Bargmann space or Bargmann–Fock space, is the space of holomorphic functions ''F'' in ''n'' complex variables satisfying the square-integr ...
—that is, for to be square-integrable with respect to a Gaussian measure— must have at most quadratic growth at infinity. From this, elementary complex analysis can be used to show that must actually be a quadratic polynomial. Thus, we obtain an explicit form of the Segal–Bargmann transform of any pure state whose Wigner function is non-negative. We can then invert the Segal–Bargmann transform to obtain the claimed form of the position wave function.
There does not appear to be any simple characterization of mixed states with non-negative Wigner functions.
The Wigner function in relation to other interpretations of quantum mechanics
It has been shown that the Wigner quasiprobability distribution function can be regarded as an -deformation
Deformation can refer to:
* Deformation (engineering), changes in an object's shape or form due to the application of a force or forces.
** Deformation (physics), such changes considered and analyzed as displacements of continuum bodies.
* Defor ...
of another phase-space distribution function that describes an ensemble of de Broglie–Bohm causal trajectories. Basil Hiley
Basil J. Hiley (born 1935), is a British quantum physicist and professor emeritus of the University of London.
Long-time colleague of David Bohm, Hiley is known for his work with Bohm on implicate orders and for his work on algebraic descriptio ...
has shown that the quasi-probability distribution may be understood as the density matrix
In quantum mechanics, a density matrix (or density operator) is a matrix that describes the quantum state of a physical system. It allows for the calculation of the probabilities of the outcomes of any measurement performed upon this system, using ...
re-expressed in terms of a mean position and momentum of a "cell" in phase space, and the de Broglie–Bohm interpretation allows one to describe the dynamics of the centers of such "cells".
There is a close connection between the description of quantum states in terms of the Wigner function and a method of quantum states reconstruction in terms of mutually unbiased bases
In quantum information theory, mutually unbiased bases in Hilbert space C''d'' are two orthonormal bases \ and \ such that the square of the magnitude of the inner product between any basis states , e_j\rangle and , f_k\rangle equals the inverse o ...
.
Uses of the Wigner function outside quantum mechanics
 * In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracing and the full wave analysis of the system. Here is replaced with in the small-angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position and angle while still including the effects of interference. If it becomes negative at any point, then simple ray tracing will not suffice to model the system. That is to say, negative values of this function are a symptom of the
* In the modelling of optical systems such as telescopes or fibre telecommunications devices, the Wigner function is used to bridge the gap between simple ray tracing and the full wave analysis of the system. Here is replaced with in the small-angle (paraxial) approximation. In this context, the Wigner function is the closest one can get to describing the system in terms of rays at position and angle while still including the effects of interference. If it becomes negative at any point, then simple ray tracing will not suffice to model the system. That is to say, negative values of this function are a symptom of the Gabor limit
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
of the classical light signal and ''not'' of quantum features of light associated with .
* In signal analysis
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as sound, images, and scientific measurements. Signal processing techniques are used to optimize transmissions, di ...
, a time-varying electrical signal, mechanical vibration, or sound wave are represented by a Wigner function. Here, is replaced with the time, and is replaced with the angular frequency , where is the regular frequency.
* In ultrafast optics
In optics, an ultrashort pulse, also known as an ultrafast event, is an electromagnetic pulse whose time duration is of the order of a picosecond (10−12 second) or less. Such pulses have a broadband optical spectrum, and can be created by m ...
, short laser pulses are characterized with the Wigner function using the same and substitutions as above. Pulse defects such as chirp (the change in frequency with time) can be visualized with the Wigner function. See adjacent figure.
* In quantum optics, and are replaced with the and quadratures, the real and imaginary components of the electric field (see coherent state
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state which has dynamics most closely resembling the oscillatory behavior of a classical harm ...
).
Measurements of the Wigner function
* Quantum tomography *Frequency-resolved optical gating Frequency-resolved optical gating (FROG) is a general method for measuring the spectral phase of ultrashort laser pulses, which range from subfemtosecond to about a nanosecond in length. Invented in 1991 by Rick Trebino and Daniel J. Kane, FROG was ...
Other related quasiprobability distributions
The Wigner distribution was the first quasiprobability distribution to be formulated, but many more followed, formally equivalent and transformable to and from it (see Transformation between distributions in time–frequency analysis). As in the case of coordinate systems, on account of varying properties, several such have with various advantages for specific applications: * Glauber P representation *Husimi Q representation
The Husimi Q representation, introduced by Kôdi Husimi in 1940, is a quasiprobability distribution commonly used in quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical prop ...
Nevertheless, in some sense, the Wigner distribution holds a privileged position among all these distributions, since it is the ''only one'' whose requisite star-product drops out (integrates out by parts to effective unity) in the evaluation of expectation values, as illustrated above, and so ''can'' be visualized as a quasiprobability measure analogous to the classical ones.
Historical note
As indicated, the formula for the Wigner function was independently derived several times in different contexts. In fact, apparently,Wigner
Eugene Paul "E. P." Wigner ( hu, Wigner Jenő Pál, ; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his con ...
was unaware that even within the context of quantum theory, it had been introduced previously by Heisenberg
Werner Karl Heisenberg () (5 December 1901 – 1 February 1976) was a German theoretical physicist and one of the main pioneers of the theory of quantum mechanics. He published his work in 1925 in a breakthrough paper. In the subsequent series ...
and Dirac
Distributed Research using Advanced Computing (DiRAC) is an integrated supercomputing facility used for research in particle physics, astronomy and cosmology in the United Kingdom. DiRAC makes use of multi-core processors and provides a variety o ...
, albeit purely formally: these two missed its significance, and that of its negative values, as they merely considered it as an approximation to the full quantum description of a system such as the atom. (Incidentally, Dirac would later become Wigner's brother-in-law, marrying his sister Manci.) Symmetrically, in most of his legendary 18-month correspondence with Moyal in the mid-1940s, Dirac was unaware that Moyal's quantum-moment generating function was effectively the Wigner function, and it was Moyal who finally brought it to his attention.Ann Moyal, (2006)"Maverick Mathematician: The Life and Science of J. E. Moyal"
ANU E-press, 2006, .
See also
*Heisenberg group
In mathematics, the Heisenberg group H, named after Werner Heisenberg, is the group of 3×3 upper triangular matrices of the form
::\begin
1 & a & c\\
0 & 1 & b\\
0 & 0 & 1\\
\end
under the operation of matrix multiplication. Elements ...
* Wigner–Weyl transform
In quantum mechanics, the Wigner–Weyl transform or Weyl–Wigner transform (after Hermann Weyl and Eugene Wigner) is the invertible mapping between functions in the quantum phase space formulation and Hilbert space operators in the Schrödin ...
* Phase space formulation
The phase-space formulation of quantum mechanics places the position ''and'' momentum variables on equal footing in phase space. In contrast, the Schrödinger picture uses the position ''or'' momentum representations (see also position and mome ...
* Moyal bracket
* Negative probability
* Optical equivalence theorem
* Modified Wigner distribution function :''Note: the Wigner distribution function is abbreviated here as WD rather than WDF as used at Wigner distribution function''
A Modified Wigner distribution function is a variation of the Wigner distribution function (WD) with reduced or removed c ...
* Cohen's class distribution function
* Wigner distribution function
The Wigner distribution function (WDF) is used in signal processing as a transform in time-frequency analysis.
The WDF was first proposed in physics to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, ...
* Transformation between distributions in time–frequency analysis
* Squeezed coherent state
In physics, a squeezed coherent state is a quantum state that is usually described by two non-commuting observables having continuous spectra of eigenvalues. Examples are position x and momentum p of a particle, and the (dimension-less) elect ...
* Bilinear time–frequency distribution
Bilinear time–frequency distributions, or quadratic time–frequency distributions, arise in a sub-field of signal analysis and signal processing called time–frequency signal processing, and, in the statistical analysis of time series data. ...
* Continuous-variable quantum information
Footnotes
References
Further reading
* M. Levanda and V. Fleurov, "Wigner quasi-distribution function for charged particles in classical electromagnetic fields", ''Annals of Physics'', 292, 199–231 (2001). .External links
wigner
Wigner function implementation in QuTiP.
Quantum Optics Gallery
Sonogram Visible Speech
GPL-licensed freeware for the Wigner quasiprobability distribution of signal files. {{DEFAULTSORT:Wigner Quasi-Probability Distribution Continuous distributions Concepts in physics Mathematical physics Exotic probabilities Articles containing video clips Quantum optics