Treemap on:
[Wikipedia]
[Google]
[Amazon]
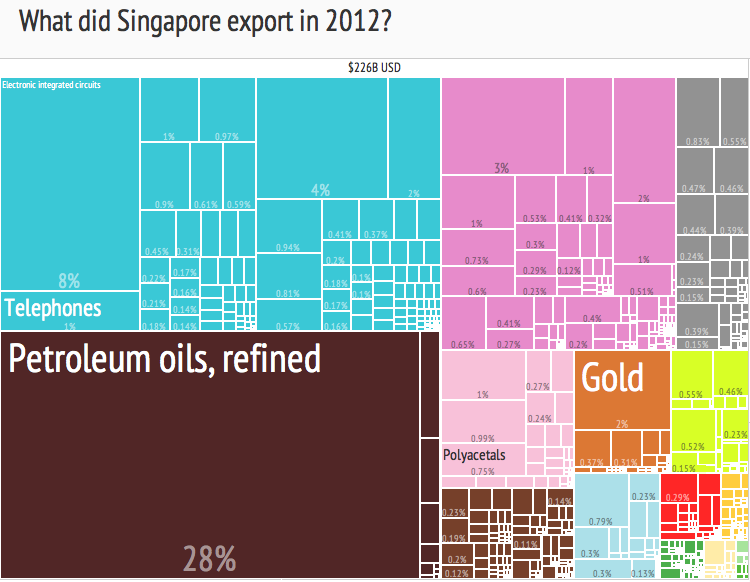 In
In
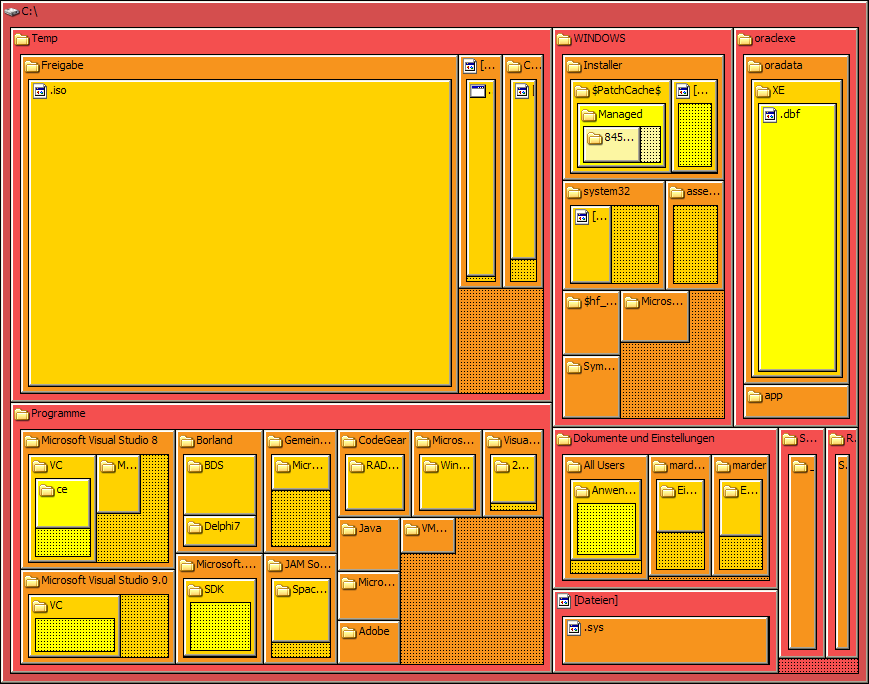 Area-based visualizations have existed for decades. For example,
Area-based visualizations have existed for decades. For example,
Treemap Art Project
produced 12 framed images for the
Every AlgoRiThm has ART in It exhibit
in Washington, DC and another set for the collection of
Treemap Art Project
produced exhibit for the National Academies in Washington, DC
An_article_by_Ben_Shneiderman
_on_the_use_of_treemaps.html" ;"title="Ben Shneiderman">An article by Ben Shneiderman
on the use of treemaps">Ben Shneiderman">An article by Ben Shneiderman
on the use of treemaps
Comprehensive survey and bibliography
of Tree Visualization techniques *
History of Treemaps
by Ben Shneiderman.
Hypermedia exploration with interactive dynamic maps
Paper by Zizi and Beaudouin-Lafon introducing the squarified treemap layout algorithm (named "improved treemap layout" at the time).
description
Live interactive treemap based on crowd-sourced discounted deals
from ''Flytail Group''
Treemap sample in English
from ''The Hive Group''
Several treemap examples
made with Macrofocus TreeMap
Visualizations using dynamic treemaps
an
by drasticdata {{Visualization User interface techniques Infographics Statistical charts and diagrams Trees (data structures) Visualization (graphics)
 In
In information visualization
Information is an abstract concept that refers to that which has the power to inform. At the most fundamental level information pertains to the interpretation of that which may be sensed. Any natural process that is not completely random, a ...
and computing
Computing is any goal-oriented activity requiring, benefiting from, or creating computing machinery. It includes the study and experimentation of algorithmic processes, and development of both hardware and software. Computing has scientific, ...
, treemapping is a method for displaying hierarchical data using nested
''Nested'' is the seventh studio album by Bronx-born singer, songwriter and pianist Laura Nyro, released in 1978 on Columbia Records.
Following on from her extensive tour to promote 1976's ''Smile'', which resulted in the 1977 live album '' Seas ...
figures, usually rectangles.
Treemaps display hierarchical ( tree-structured) data as a set of nested rectangles. Each branch of the tree is given a rectangle, which is then tiled with smaller rectangles representing sub-branches. A leaf node's rectangle has an area proportional to a specified dimension of the data. Often the leaf nodes are colored to show a separate dimension of the data.
When the color and size dimensions are correlated in some way with the tree structure, one can often easily see patterns that would be difficult to spot in other ways, such as whether a certain color is particularly relevant. A second advantage of treemaps is that, by construction, they make efficient use of space. As a result, they can legibly display thousands of items on the screen simultaneously.
Tiling algorithms
To create a treemap, one must define atiling
Tiling may refer to:
*The physical act of laying tiles
* Tessellations
Computing
*The compiler optimization of loop tiling
*Tiled rendering, the process of subdividing an image by regular grid
*Tiling window manager
People
*Heinrich Sylvester T ...
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing ...
, that is, a way to divide a region into sub-regions of specified areas. Ideally, a treemap algorithm would create regions that satisfy the following criteria:
# A small aspect ratio—ideally close to one. Regions with a small aspect ratio (i.e, fat objects) are easier to perceive.
# Preserve some sense of the ordering in the input data (ordered).
# Change to reflect changes in the underlying data (high stability).
Unfortunately, these properties have an inverse relationship. As the aspect ratio is optimized, the order of placement becomes less predictable. As the order becomes more stable, the aspect ratio is degraded.
Rectangular treemaps
To date, fifteen primary rectangular treemap algorithms have been developed:Convex treemaps
Rectangular treemaps have the disadvantage that their aspect ratio might be arbitrarily high in the worst case. As a simple example, if the tree root has only two children, one with weight and one with weight , then the aspect ratio of the smaller child will be , which can be arbitrarily high. To cope with this problem, several algorithms have been proposed that use regions that are generalconvex polygon
In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is a ...
s, not necessarily rectangular.
Convex treemaps were developed in several steps, each step improved the upper bound on the aspect ratio. The bounds are given as a function of - the total number of nodes in the tree, and - the total depth of the tree.
#Onak and Sidiropoulos proved an upper bound of .
#De-Berg and Onak and Sidiropoulos improve the upper bound to , and prove a lower bound of .
#De-Berg and Speckmann and van-der-Weele. Conference version: improve the upper bound to , matching the theoretical lower bound. (For the special case where the depth is 1, they present an algorithm that uses only four classes of 45-degree-polygons (rectangles, right-angled triangles, right-angled trapezoids and 45-degree pentagons), and guarantees an aspect ratio of at most 34/7.)
The latter two algorithms operate in two steps (greatly simplified for clarity):
# The original tree is converted to a binary tree: each node with more than two children is replaced by a sub-tree in which each node has exactly two children.
# Each region representing a node (starting from the root) is divided to two, using a line that keeps the angles between edges as large as possible. It is possible to prove that, if all edges of a convex polygon are separated by an angle of at least , then its aspect ratio is . It is possible to ensure that, in a tree of depth , the angle is divided by a factor of at most , hence the aspect ratio guarantee.
Orthoconvex treemaps
In convex treemaps, the aspect ratio cannot be constant - it grows with the depth of the tree. To attain a constant aspect-ratio, Orthoconvex treemaps can be used. There, all regions areorthoconvex
In geometry, a set is defined to be orthogonally convex if, for every line that is parallel to one of standard basis vectors, the intersection of with is empty, a point, or a single segment. The term "orthogonal" refers to corresponding C ...
rectilinear polygon
A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.
In many cases another definition is ...
s with aspect ratio at most 64; and the leaves are either rectangles with aspect ratio at most 8, or L-shapes or S-shapes with aspect ratio at most 32.
For the special case where the depth is 1, they present an algorithm that uses only rectangles and L-shapes, and the aspect ratio is at most ; the internal nodes use only rectangles with aspect ratio at most .
Other treemaps
;Voronoi Treemaps:. based onVoronoi diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed ...
calculations. The algorithm is iterative and does not give any upper bound on the aspect ratio.
;Jigsaw Treemaps.: based on the geometry of space-filling curves. They assume that the weights are integers and that their sum is a square number. The regions of the map are rectilinear polygon
A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.
In many cases another definition is ...
s and highly non-ortho-convex. Their aspect ratio is guaranteed to be at most 4.
;GosperMaps:. based on the geometry of Gosper curve
The Gosper curve, named after Bill Gosper, also known as the Peano-Gosper Curve and the flowsnake (a spoonerism of snowflake), is a space-filling curve whose limit set is rep-7. It is a fractal curve similar in its construction to the dragon c ...
s. It is ordered and stable, but has a very high aspect ratio.
History
 Area-based visualizations have existed for decades. For example,
Area-based visualizations have existed for decades. For example, mosaic plot
A mosaic is a pattern or image made of small regular or irregular pieces of colored stone, glass or ceramic, held in place by plaster/mortar, and covering a surface. Mosaics are often used as floor and wall decoration, and were particularly pop ...
s (also known as Marimekko diagrams) use rectangular tilings to show joint distributions (i.e., most commonly they are essentially stacked column plots where the columns are of different widths). The main distinguishing feature of a treemap, however, is the recursive construction that allows it to be extended to hierarchical data with any number of levels. This idea was invented by professor Ben Shneiderman
Ben Shneiderman (born August 21, 1947) is an American computer scientist, a Distinguished University Professor in the University of Maryland Department of Computer Science, which is part of the University of Maryland College of Computer, Mathem ...
at the University of Maryland Human – Computer Interaction Lab in the early 1990s.
Shneiderman and his collaborators then deepened the idea by introducing a variety of interactive techniques for filtering and adjusting treemaps.
These early treemaps all used the simple "slice-and-dice" tiling algorithm. Despite many desirable properties (it is stable, preserves ordering, and is easy to implement), the slice-and-dice method often produces tilings with many long, skinny rectangles. In 1994 Mountaz Hascoet and Michel Beaudouin-Lafon
Michel Beaudouin-Lafon (20 July 1961) is a French computer scientist working in the field of human–computer interaction. He received his PhD from the Paris-Sud 11 University (which is now Paris-Saclay University) in 1985. He is currently profess ...
invented a "squarifying" algorithm, later popularized by Jarke van Wijk
Jarke J. (Jack) van Wijk (born 1959) is a Dutch computer scientist, a professor in the Department of Mathematics and Computer Science at the Eindhoven University of Technology, and an expert in information visualization.
Biography
Van Wijk recei ...
, that created tilings whose rectangles were closer to square. In 1999 Martin Wattenberg used a variation of the "squarifying" algorithm that he called "pivot and slice" to create the first Web-based treemap, the SmartMoney Map of the Market, which displayed data on hundreds of companies in the U.S. stock market. Following its launch, treemaps enjoyed a surge of interest, especially in financial contexts.
A third wave of treemap innovation came around 2004, after Marcos Weskamp Marcos may refer to:
People with the given name ''Marcos''
*Marcos (given name)
Sports
;Surnamed
* Dayton Marcos, Negro league baseball team from Dayton, Ohio (early twentieth-century)
* Dimitris Markos, Greek footballer
* Nélson Marcos, Portugu ...
created the Newsmap, a treemap that displayed news headlines. This example of a non-analytical treemap inspired many imitators, and introduced treemaps to a new, broad audience. In recent years, treemaps have made their way into the mainstream media, including usage by the New York Times.
ThTreemap Art Project
produced 12 framed images for the
National Academies (United States)
The National Academies of Sciences, Engineering, and Medicine (also known as NASEM or the National Academies) are the collective scientific national academy of the United States. The name is used interchangeably in two senses: (1) as an umbrell ...
, shown thEvery AlgoRiThm has ART in It exhibit
in Washington, DC and another set for the collection of
Museum of Modern Art
The Museum of Modern Art (MoMA) is an art museum located in Midtown Manhattan, New York City, on 53rd Street between Fifth and Sixth Avenues.
It plays a major role in developing and collecting modern art, and is often identified as one of ...
in New York.
See also
*Disk space analyzer
A disk utility is a utility program that allows a user to perform various functions on a computer disk, such as disk partitioning and logical volume management, as well as multiple smaller tasks such as changing drive letters and other mount po ...
* Information visualization
Information is an abstract concept that refers to that which has the power to inform. At the most fundamental level information pertains to the interpretation of that which may be sensed. Any natural process that is not completely random, a ...
*List of countries by economic complexity
This list orders countries by their economic complexity index (ECI), as it was defined and calculated by Cesar A. Hidalgo and Ricardo Hausmann.
Country rankings
Factors affecting differences between countries
As an illustration, we can ob ...
, which includes a list of Products Exports Treemaps.
* Marimekko Chart, a similar concept with one level of explicit hierarchy.
References
External links
Treemap Art Project
produced exhibit for the National Academies in Washington, DC
An_article_by_Ben_Shneiderman
_on_the_use_of_treemaps.html" ;"title="Ben Shneiderman">An article by Ben Shneiderman
on the use of treemaps">Ben Shneiderman">An article by Ben Shneiderman
on the use of treemaps
Comprehensive survey and bibliography
of Tree Visualization techniques *
History of Treemaps
by Ben Shneiderman.
Hypermedia exploration with interactive dynamic maps
Paper by Zizi and Beaudouin-Lafon introducing the squarified treemap layout algorithm (named "improved treemap layout" at the time).
description
Live interactive treemap based on crowd-sourced discounted deals
from ''Flytail Group''
Treemap sample in English
from ''The Hive Group''
Several treemap examples
made with Macrofocus TreeMap
Visualizations using dynamic treemaps
an
by drasticdata {{Visualization User interface techniques Infographics Statistical charts and diagrams Trees (data structures) Visualization (graphics)