Symmetrical on:
[Wikipedia]
[Google]
[Amazon]


 Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In
 A geometric shape or object is symmetric if it can be divided into two or more identical pieces that are arranged in an organized fashion. This means that an object is symmetric if there is a transformation that moves individual pieces of the object, but doesn't change the overall shape. The type of symmetry is determined by the way the pieces are organized, or by the type of transformation:
* An object has
A geometric shape or object is symmetric if it can be divided into two or more identical pieces that are arranged in an organized fashion. This means that an object is symmetric if there is a transformation that moves individual pieces of the object, but doesn't change the overall shape. The type of symmetry is determined by the way the pieces are organized, or by the type of transformation:
* An object has

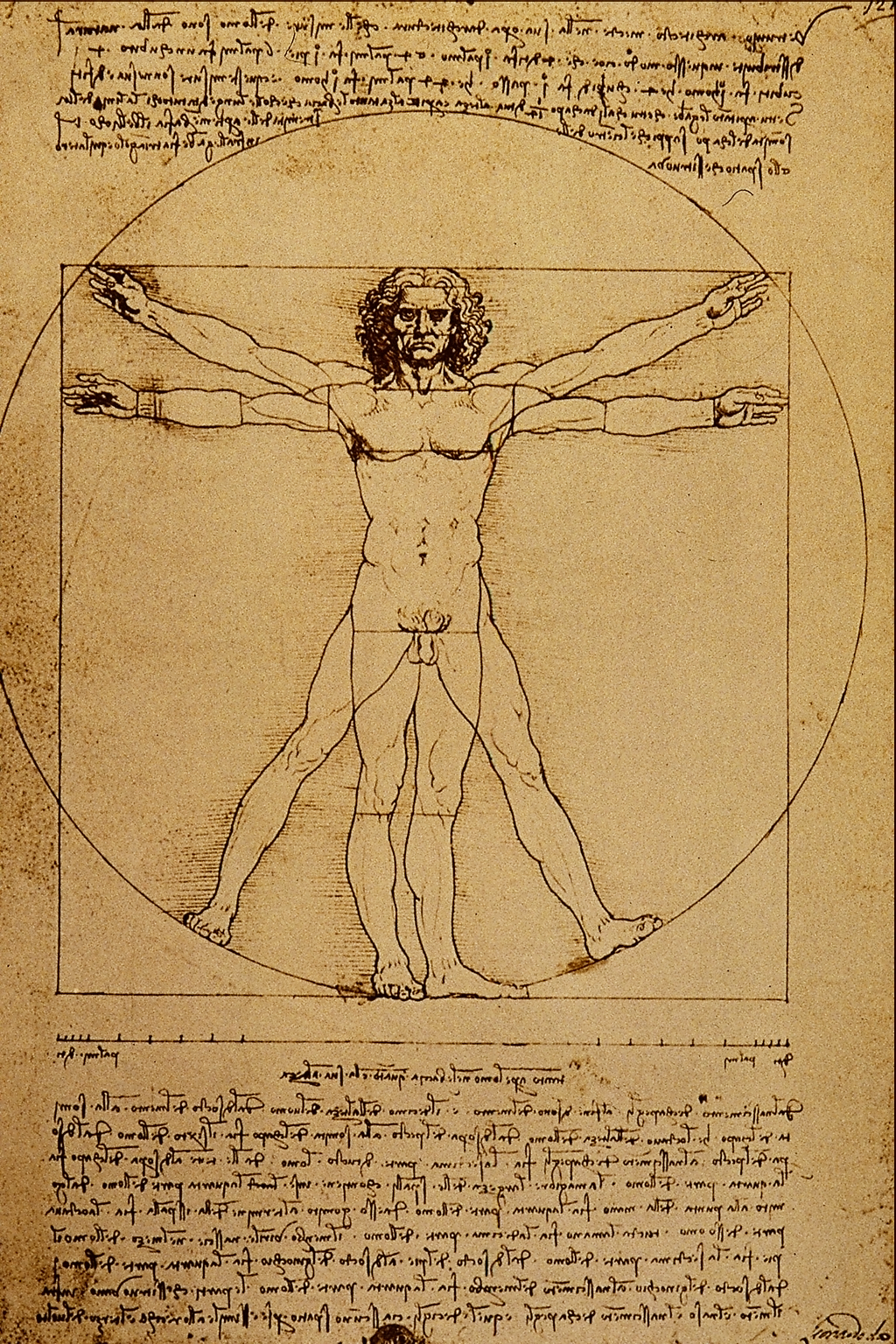 In biology, the notion of symmetry is mostly used explicitly to describe body shapes.
In biology, the notion of symmetry is mostly used explicitly to describe body shapes.
 There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.

 Symmetry finds its ways into architecture at every scale, from the overall external views of buildings such as Gothic
Symmetry finds its ways into architecture at every scale, from the overall external views of buildings such as Gothic
 Since the earliest uses of pottery wheels to help shape clay vessels, pottery has had a strong relationship to symmetry. Pottery created using a wheel acquires full rotational symmetry in its cross-section, while allowing substantial freedom of shape in the vertical direction. Upon this inherently symmetrical starting point, potters from ancient times onwards have added patterns that modify the rotational symmetry to achieve visual objectives.
Cast metal vessels lacked the inherent rotational symmetry of wheel-made pottery, but otherwise provided a similar opportunity to decorate their surfaces with patterns pleasing to those who used them. The ancient Chinese, for example, used symmetrical patterns in their bronze castings as early as the 17th century BC. Bronze vessels exhibited both a bilateral main motif and a repetitive translated border design.
Since the earliest uses of pottery wheels to help shape clay vessels, pottery has had a strong relationship to symmetry. Pottery created using a wheel acquires full rotational symmetry in its cross-section, while allowing substantial freedom of shape in the vertical direction. Upon this inherently symmetrical starting point, potters from ancient times onwards have added patterns that modify the rotational symmetry to achieve visual objectives.
Cast metal vessels lacked the inherent rotational symmetry of wheel-made pottery, but otherwise provided a similar opportunity to decorate their surfaces with patterns pleasing to those who used them. The ancient Chinese, for example, used symmetrical patterns in their bronze castings as early as the 17th century BC. Bronze vessels exhibited both a bilateral main motif and a repetitive translated border design.
 A long tradition of the use of symmetry in
A long tradition of the use of symmetry in
 As
As
 Symmetries appear in the design of objects of all kinds. Examples include
Symmetries appear in the design of objects of all kinds. Examples include
File:Major and minor triads, triangles.png, Major and minor triads on the white piano keys are symmetrical to the D. (compare article) (file)
poly 35 442 35 544 179 493 root of A minor triad
poly 479 462 446 493 479 526 513 492 third of A minor triad
poly 841 472 782 493 840 514 821 494 fifth of A minor triad
poly 926 442 875 460 906 493 873 525 926 545 fifth of A minor triad
poly 417 442 417 544 468 525 437 493 469 459 root of C major triad
poly 502 472 522 493 502 514 560 493 root of C major triad
poly 863 462 830 493 863 525 895 493 third of C major triad
poly 1303 442 1160 493 1304 544 fifth of C major triad
poly 280 406 264 413 282 419 275 413 fifth of E minor triad
poly 308 397 293 403 301 412 294 423 309 428 fifth of E minor triad
poly 844 397 844 428 886 413 root of E minor triad
poly 1240 404 1230 412 1239 422 1250 412 third of E minor triad
poly 289 404 279 413 288 422 300 413 third of G major triad
poly 689 398 646 413 689 429 fifth of G major triad
poly 1221 397 1222 429 1237 423 1228 414 1237 403 root of G major triad
poly 1249 406 1254 413 1249 418 1265 413 root of G major triad
poly 89 567 73 573 90 579 86 573 fifth of D minor triad
poly 117 558 102 563 111 572 102 583 118 589 fifth of D minor triad
poly 650 558 650 589 693 573 root of D minor triad
poly 1050 563 1040 574 1050 582 1061 574 third of D minor triad
poly 98 565 88 573 98 583 110 574 third of F major triad
poly 498 558 455 573 498 589 fifth of F major triad
poly 1031 557 1031 589 1047 583 1038 574 1046 563 root of F major triad
poly 1075 573 1059 580 1064 573 1058 567 root of F major triad
desc none
Symmetry is not restricted to the visual arts. Its role in the history of
International Symmetry Association (ISA)Dutch: Symmetry Around a Point in the Plane
Symmetry
BBC Radio 4 discussion with Fay Dowker, Marcus du Sautoy & Ian Stewart (''In Our Time'', Apr. 19, 2007) {{Patterns in nature Geometry Theoretical physics Artistic techniques Aesthetics
 Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, "symmetry" has a more precise definition, and is usually used to refer to an object that is invariant under some transformations; including translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transla ...
, reflection Reflection or reflexion may refer to:
Science and technology
* Reflection (physics), a common wave phenomenon
** Specular reflection, reflection from a smooth surface
*** Mirror image, a reflection in a mirror or in water
** Signal reflection, in ...
, rotation
Rotation, or spin, is the circular movement of an object around a '' central axis''. A two-dimensional rotating object has only one possible central axis and can rotate in either a clockwise or counterclockwise direction. A three-dimensional ...
or scaling. Although these two meanings of "symmetry" can sometimes be told apart, they are intricately related, and hence are discussed together in this article.
Mathematical symmetry may be observed with respect to the passage of time
Time is the continued sequence of existence and event (philosophy), events that occurs in an apparently irreversible process, irreversible succession from the past, through the present, into the future. It is a component quantity of various me ...
; as a spatial relationship; through geometric transformation
In mathematics, a geometric transformation is any bijection of a set to itself (or to another such set) with some salient geometrical underpinning. More specifically, it is a function whose domain and range are sets of points — most often b ...
s; through other kinds of functional transformations; and as an aspect of abstract object
In metaphysics, the distinction between abstract and concrete refers to a divide between two types of entities. Many philosophers hold that this difference has fundamental metaphysical significance. Examples of concrete objects include plants, h ...
s, including theoretic models, language
Language is a structured system of communication. The structure of a language is its grammar and the free components are its vocabulary. Languages are the primary means by which humans communicate, and may be conveyed through a variety of ...
, and music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
.
This article describes symmetry from three perspectives: in mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, including geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, the most familiar type of symmetry for many people; in science
Science is a systematic endeavor that builds and organizes knowledge in the form of testable explanations and predictions about the universe.
Science may be as old as the human species, and some of the earliest archeological evidence ...
and nature
Nature, in the broadest sense, is the physical world or universe. "Nature" can refer to the phenomena of the physical world, and also to life in general. The study of nature is a large, if not the only, part of science. Although humans are ...
; and in the arts, covering architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and constructing buildings ...
, art and music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
.
The opposite of symmetry is asymmetry
Asymmetry is the absence of, or a violation of, symmetry (the property of an object being invariant to a transformation, such as reflection). Symmetry is an important property of both physical and abstract systems and it may be displayed in pre ...
, which refers to the absence or a violation of symmetry.
In mathematics
In geometry
reflectional symmetry
In mathematics, reflection symmetry, line symmetry, mirror symmetry, or mirror-image symmetry is symmetry with respect to a reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.
In 2D th ...
(line or mirror symmetry) if there is a line (or in 3D a plane) going through it which divides it into two pieces that are mirror images of each other.
*An object has rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which ...
if the object can be rotated about a fixed point (or in 3D about a line) without changing the overall shape.
*An object has translational symmetry
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equati ...
if it can be translated
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. The English language draws a terminological distinction (which does not exist in every language) between ''transla ...
(moving every point of the object by the same distance) without changing its overall shape.
*An object has helical symmetry
In geometry, an object has symmetry if there is an operation or transformation (such as translation, scaling, rotation or reflection) that maps the figure/object onto itself (i.e., the object has an invariance under the transform). Thus, a symme ...
if it can be simultaneously translated and rotated in three-dimensional space along a line known as a screw axis
A screw axis (helical axis or twist axis) is a line that is simultaneously the axis of rotation and the line along which translation of a body occurs. Chasles' theorem shows that each Euclidean displacement in three-dimensional space has a scr ...
.
*An object has scale symmetry if it does not change shape when it is expanded or contracted. Fractals
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illus ...
also exhibit a form of scale symmetry, where smaller portions of the fractal are similar in shape to larger portions.
*Other symmetries include glide reflection
In 2-dimensional geometry, a glide reflection (or transflection) is a symmetry operation that consists of a reflection over a line and then translation along that line, combined into a single operation. The intermediate step between reflecti ...
symmetry (a reflection followed by a translation) and rotoreflection
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicul ...
symmetry (a combination of a rotation and a reflection).
In logic
Adyadic relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over sets and is a new set of ordered pairs consisting of elements in and ...
''R'' = ''S'' × ''S'' is symmetric if for all elements ''a'', ''b'' in ''S'', whenever it is true that ''Rab'', it is also true that ''Rba''. Thus, the relation "is the same age as" is symmetric, for if Paul is the same age as Mary, then Mary is the same age as Paul.
In propositional logic, symmetric binary logical connective
In logic, a logical connective (also called a logical operator, sentential connective, or sentential operator) is a logical constant. They can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary ...
s include ''and
or AND may refer to:
Logic, grammar, and computing
* Conjunction (grammar), connecting two words, phrases, or clauses
* Logical conjunction in mathematical logic, notated as "∧", "⋅", "&", or simple juxtaposition
* Bitwise AND, a boolea ...
'' (∧, or &), '' or'' (∨, or , ) and ''if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bic ...
'' (↔), while the connective ''if'' (→) is not symmetric. Other symmetric logical connectives include '' nand'' (not-and, or ⊼), ''xor
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , ...
'' (not-biconditional, or ⊻), and '' nor'' (not-or, or ⊽).
Other areas of mathematics
Generalizing from geometrical symmetry in the previous section, one can say that amathematical object
A mathematical object is an abstract concept arising in mathematics.
In the usual language of mathematics, an ''object'' is anything that has been (or could be) formally defined, and with which one may do deductive reasoning and mathematical p ...
is ''symmetric'' with respect to a given mathematical operation
In mathematics, an operation is a Function (mathematics), function which takes zero or more input values (also called "''operands''" or "arguments") to a well-defined output value. The number of operands is the arity of the operation.
The most c ...
, if, when applied to the object, this operation preserves some property of the object. The set of operations that preserve a given property of the object form a group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic ide ...
.
In general, every kind of structure in mathematics will have its own kind of symmetry. Examples include even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power ser ...
in calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
, symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group ...
s in abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures. Algebraic structures include groups, rings, fields, modules, vector spaces, lattices, and algebras over a field. The ter ...
, symmetric matrices in linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matrice ...
, and Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the po ...
s in Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to ...
. In statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, indust ...
, symmetry also manifests as symmetric probability distributions, and as skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal ...
—the asymmetry of distributions.
In science and nature
In physics
Symmetry in physics has been generalized to mean invariance—that is, lack of change—under any kind of transformation, for example arbitrary coordinate transformations. This concept has become one of the most powerful tools oftheoretical physics
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experim ...
, as it has become evident that practically all laws of nature originate in symmetries. In fact, this role inspired the Nobel laureate PW Anderson to write in his widely read 1972 article ''More is Different'' that "it is only slightly overstating the case to say that physics is the study of symmetry." See Noether's theorem
Noether's theorem or Noether's first theorem states that every differentiable symmetry of the action of a physical system with conservative forces has a corresponding conservation law. The theorem was proven by mathematician Emmy Noether ...
(which, in greatly simplified form, states that for every continuous mathematical symmetry, there is a corresponding conserved quantity such as energy or momentum; a conserved current, in Noether's original language); and also, Wigner's classification
In mathematics and theoretical physics, Wigner's classification
is a classification of the nonnegative ~ (~E \ge 0~)~ energy irreducible unitary representations of the Poincaré group which have either finite or zero mass eigenvalues. (Since thi ...
, which says that the symmetries of the laws of physics determine the properties of the particles found in nature.
Important symmetries in physics include continuous symmetries and discrete symmetries
In mathematics and geometry, a discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square ...
of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differ ...
; internal symmetries
In physics, a symmetry of a physical system is a physical or mathematical feature of the system (observed or intrinsic) that is preserved or remains unchanged under some transformation.
A family of particular transformations may be ''continu ...
of particles; and supersymmetry
In a supersymmetric theory the equations for force and the equations for matter are identical. In theoretical and mathematical physics, any theory with this property has the principle of supersymmetry (SUSY). Dozens of supersymmetric theories ...
of physical theories.
In biology

 In biology, the notion of symmetry is mostly used explicitly to describe body shapes.
In biology, the notion of symmetry is mostly used explicitly to describe body shapes. Bilateral animals
The Bilateria or bilaterians are animals with bilateral symmetry as an embryo, i.e. having a left and a right side that are mirror images of each other. This also means they have a head and a tail (anterior-posterior axis) as well as a belly and ...
, including humans, are more or less symmetric with respect to the sagittal plane
The sagittal plane (; also known as the longitudinal plane) is an anatomical plane that divides the body into right and left sections. It is perpendicular to the transverse and coronal planes. The plane may be in the center of the body and divid ...
which divides the body into left and right halves. Animals that move in one direction necessarily have upper and lower sides, head and tail ends, and therefore a left and a right. The head becomes specialized with a mouth and sense organs, and the body becomes bilaterally symmetric for the purpose of movement, with symmetrical pairs of muscles and skeletal elements, though internal organs often remain asymmetric.
Plants and sessile (attached) animals such as sea anemone
Sea anemones are a group of predatory marine invertebrates of the order Actiniaria. Because of their colourful appearance, they are named after the '' Anemone'', a terrestrial flowering plant. Sea anemones are classified in the phylum Cnidaria, ...
s often have radial or rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which ...
, which suits them because food or threats may arrive from any direction. Fivefold symmetry is found in the echinoderms
An echinoderm () is any member of the phylum Echinodermata (). The adults are recognisable by their (usually five-point) radial symmetry, and include starfish, brittle stars, sea urchins, sand dollars, and sea cucumbers, as well as the ...
, the group that includes starfish
Starfish or sea stars are star-shaped echinoderms belonging to the class Asteroidea (). Common usage frequently finds these names being also applied to ophiuroids, which are correctly referred to as brittle stars or basket stars. Starfish a ...
, sea urchin
Sea urchins () are spiny, globular echinoderms in the class Echinoidea. About 950 species of sea urchin live on the seabed of every ocean and inhabit every depth zone from the intertidal seashore down to . The spherical, hard shells (tests) o ...
s, and sea lilies
Crinoids are marine animals that make up the class Crinoidea. Crinoids that are attached to the sea bottom by a stalk in their adult form are commonly called sea lilies, while the unstalked forms are called feather stars or comatulids, which ar ...
.
In biology, the notion of symmetry is also used as in physics, that is to say to describe the properties of the objects studied, including their interactions. A remarkable property of biological evolution is the changes of symmetry corresponding to the appearance of new parts and dynamics.
In chemistry
Symmetry is important tochemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a natural science that covers the elements that make up matter to the compounds made of atoms, molecules and ions: their composition, structure, proper ...
because it undergirds essentially all ''specific'' interactions between molecules in nature (i.e., via the interaction of natural and human-made chiral
Chirality is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is distinguishable from i ...
molecules with inherently chiral biological systems). The control of the symmetry
Symmetry (from grc, συμμετρία "agreement in dimensions, due proportion, arrangement") in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definiti ...
of molecules produced in modern chemical synthesis
As a topic of chemistry, chemical synthesis (or combination) is the artificial execution of chemical reactions to obtain one or several products. This occurs by physical and chemical manipulations usually involving one or more reactions. In mod ...
contributes to the ability of scientists to offer therapeutic interventions with minimal side effects
In medicine, a side effect is an effect, whether therapeutic or adverse, that is secondary to the one intended; although the term is predominantly employed to describe adverse effects, it can also apply to beneficial, but unintended, consequenc ...
. A rigorous understanding of symmetry explains fundamental observations in quantum chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions ...
, and in the applied areas of spectroscopy
Spectroscopy is the field of study that measures and interprets the electromagnetic spectra that result from the interaction between electromagnetic radiation and matter as a function of the wavelength or frequency of the radiation. Matter ...
and crystallography
Crystallography is the experimental science of determining the arrangement of atoms in crystalline solids. Crystallography is a fundamental subject in the fields of materials science and solid-state physics ( condensed matter physics). The wor ...
. The theory and application of symmetry to these areas of physical science
Physical science is a branch of natural science that studies non-living systems, in contrast to life science. It in turn has many branches, each referred to as a "physical science", together called the "physical sciences".
Definition
Phys ...
draws heavily on the mathematical area of group theory
In abstract algebra, group theory studies the algebraic structures known as groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen ...
.
In psychology and neuroscience
For a human observer, some symmetry types are more salient than others, in particular the most salient is a reflection with a vertical axis, like that present in the human face.Ernst Mach
Ernst Waldfried Josef Wenzel Mach ( , ; 18 February 1838 – 19 February 1916) was a Moravian-born Austrian physicist and philosopher, who contributed to the physics of shock waves. The ratio of one's speed to that of sound is named the Mach n ...
made this observation in his book "The analysis of sensations" (1897), and this implies that perception of symmetry is not a general response to all types of regularities. Both behavioural and neurophysiological studies have confirmed the special sensitivity to reflection symmetry in humans and also in other animals. Early studies within the Gestalt tradition suggested that bilateral symmetry was one of the key factors in perceptual grouping
Grouping may refer to:
* Muenchian grouping
* Principles of grouping
* Railways Act 1921, also known as Grouping Act, a reorganisation of the British railway system
* Grouping (firearms), the pattern of multiple shots from a sidearm
See also ...
. This is known as the Law of Symmetry. The role of symmetry in grouping and figure/ground organization has been confirmed in many studies. For instance, detection of reflectional symmetry is faster when this is a property of a single object. Studies of human perception and psychophysics have shown that detection of symmetry is fast, efficient and robust to perturbations. For example, symmetry can be detected with presentations between 100 and 150 milliseconds.
More recent neuroimaging studies have documented which brain regions are active during perception of symmetry. Sasaki et al. used functional magnetic resonance imaging (fMRI) to compare responses for patterns with symmetrical or random dots. A strong activity was present in extrastriate regions of the occipital cortex but not in the primary visual cortex. The extrastriate regions included V3A, V4, V7, and the lateral occipital complex (LOC). Electrophysiological studies have found a late posterior negativity that originates from the same areas. In general, a large part of the visual system seems to be involved in processing visual symmetry, and these areas involve similar networks to those responsible for detecting and recognising objects.
In social interactions
People observe the symmetrical nature, often including asymmetrical balance, of social interactions in a variety of contexts. These include assessments of reciprocity,empathy
Empathy is the capacity to understand or feel what another person is experiencing from within their frame of reference, that is, the capacity to place oneself in another's position. Definitions of empathy encompass a broad range of social, co ...
, sympathy
Sympathy is the perception of, understanding of, and reaction to the distress or need of another life form. According to David Hume, this sympathetic concern is driven by a switch in viewpoint from a personal perspective to the perspective of an ...
, apology, dialogue
Dialogue (sometimes spelled dialog in American and British English spelling differences, American English) is a written or spoken conversational exchange between two or more people, and a literature, literary and theatrical form that depicts suc ...
, respect, justice
Justice, in its broadest sense, is the principle that people receive that which they deserve, with the interpretation of what then constitutes "deserving" being impacted upon by numerous fields, with many differing viewpoints and perspective ...
, and revenge
Revenge is committing a harmful action against a person or group in response to a grievance, be it real or perceived. Francis Bacon described revenge as a kind of "wild justice" that "does... offend the law ndputteth the law out of office." P ...
.
Reflective equilibrium is the balance that may be attained through deliberative mutual adjustment among general principles and specific judgment
Judgement (or US spelling judgment) is also known as ''adjudication'', which means the evaluation of evidence to make a decision. Judgement is also the ability to make considered decisions. The term has at least five distinct uses. Aristotle s ...
s.
Symmetrical interactions send the moral
A moral (from Latin ''morālis'') is a message that is conveyed or a lesson to be learned from a story or event. The moral may be left to the hearer, reader, or viewer to determine for themselves, or may be explicitly encapsulated in a maxim. ...
message "we are all the same" while asymmetrical interactions may send the message "I am special; better than you." Peer relationships, such as can be governed by the golden rule, are based on symmetry, whereas power relationships are based on asymmetry. Symmetrical relationships can to some degree be maintained by simple (game theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has appli ...
) strategies seen in symmetric games such as tit for tat
Tit for tat is an English saying meaning "equivalent retaliation". It developed from "tip for tap", first recorded in 1558.
It is also a highly effective strategy in game theory. An intelligent agent, agent using this strategy will first coope ...
.
In the arts
 There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
There exists a list of journals and newsletters known to deal, at least in part, with symmetry and the arts.
In architecture

cathedral
A cathedral is a church that contains the ''cathedra'' () of a bishop, thus serving as the central church of a diocese, conference, or episcopate. Churches with the function of "cathedral" are usually specific to those Christian denominations ...
s and The White House
The White House is the official residence and workplace of the president of the United States. It is located at 1600 Pennsylvania Avenue NW in Washington, D.C., and has been the residence of every U.S. president since John Adams in 180 ...
, through the layout of the individual floor plan
In architecture and building engineering, a floor plan is a technical drawing to scale, showing a view from above, of the relationships between rooms, spaces, traffic patterns, and other physical features at one level of a structure.
Dimensio ...
s, and down to the design of individual building elements such as tile mosaics. Islam
Islam (; ar, ۘالِإسلَام, , ) is an Abrahamic monotheistic religion centred primarily around the Quran, a religious text considered by Muslims to be the direct word of God (or '' Allah'') as it was revealed to Muhammad, the ...
ic buildings such as the Taj Mahal
The Taj Mahal (; ) is an Islamic ivory-white marble mausoleum on the right bank of the river Yamuna in the Indian city of Agra. It was commissioned in 1631 by the Mughal emperor Shah Jahan () to house the tomb of his favourite wife, ...
and the Lotfollah mosque
Sheikh Lotfollah Mosque ( fa, مسجد شیخ لطف الله) is one of the masterpieces of Iranian architecture that was built during the Safavid Empire, standing on the eastern side of Naqsh-i Jahan Square, Esfahan, Iran. Construction of th ...
make elaborate use of symmetry both in their structure and in their ornamentation. Moorish buildings like the Alhambra
The Alhambra (, ; ar, الْحَمْرَاء, Al-Ḥamrāʾ, , ) is a palace and fortress complex located in Granada, Andalusia, Spain. It is one of the most famous monuments of Islamic architecture and one of the best-preserved palaces of ...
are ornamented with complex patterns made using translational and reflection symmetries as well as rotations.
It has been said that only bad architects rely on a "symmetrical layout of blocks, masses and structures"; Modernist architecture
Modern architecture, or modernist architecture, was an architectural movement or architectural style based upon new and innovative technologies of construction, particularly the use of glass, steel, and reinforced concrete; the idea that form ...
, starting with International style, relies instead on "wings and balance of masses".
In pottery and metal vessels
 Since the earliest uses of pottery wheels to help shape clay vessels, pottery has had a strong relationship to symmetry. Pottery created using a wheel acquires full rotational symmetry in its cross-section, while allowing substantial freedom of shape in the vertical direction. Upon this inherently symmetrical starting point, potters from ancient times onwards have added patterns that modify the rotational symmetry to achieve visual objectives.
Cast metal vessels lacked the inherent rotational symmetry of wheel-made pottery, but otherwise provided a similar opportunity to decorate their surfaces with patterns pleasing to those who used them. The ancient Chinese, for example, used symmetrical patterns in their bronze castings as early as the 17th century BC. Bronze vessels exhibited both a bilateral main motif and a repetitive translated border design.
Since the earliest uses of pottery wheels to help shape clay vessels, pottery has had a strong relationship to symmetry. Pottery created using a wheel acquires full rotational symmetry in its cross-section, while allowing substantial freedom of shape in the vertical direction. Upon this inherently symmetrical starting point, potters from ancient times onwards have added patterns that modify the rotational symmetry to achieve visual objectives.
Cast metal vessels lacked the inherent rotational symmetry of wheel-made pottery, but otherwise provided a similar opportunity to decorate their surfaces with patterns pleasing to those who used them. The ancient Chinese, for example, used symmetrical patterns in their bronze castings as early as the 17th century BC. Bronze vessels exhibited both a bilateral main motif and a repetitive translated border design.
In carpets and rugs
 A long tradition of the use of symmetry in
A long tradition of the use of symmetry in carpet
A carpet is a textile floor covering typically consisting of an upper layer of pile attached to a backing. The pile was traditionally made from wool, but since the 20th century synthetic fibers such as polypropylene, nylon, or polyester ...
and rug patterns spans a variety of cultures. American Navajo
The Navajo (; British English: Navaho; nv, Diné or ') are a Native Americans in the United States, Native American people of the Southwestern United States.
With more than 399,494 enrolled tribal members , the Navajo Nation is the largest fe ...
Indians used bold diagonals and rectangular motifs. Many Oriental rugs
An oriental rug is a heavy textile made for a wide variety of utilitarian and symbolic purposes and produced in " Oriental countries" for home use, local sale, and export.
Oriental carpets can be pile woven or flat woven without pile, using v ...
have intricate reflected centers and borders that translate a pattern. Not surprisingly, rectangular rugs have typically the symmetries of a rectangle
In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal (360°/4 = 90°); or a parallelogram contain ...
—that is, motifs that are reflected across both the horizontal and vertical axes (see ).
In quilts
quilt
A quilt is a multi-layered textile, traditionally composed of two or more layers of fabric or fiber. Commonly three layers are used with a filler material. These layers traditionally include a woven cloth top, a layer of batting or wadding, ...
s are made from square blocks (usually 9, 16, or 25 pieces to a block) with each smaller piece usually consisting of fabric triangles, the craft lends itself readily to the application of symmetry.
In other arts and crafts
beadwork
Beadwork is the art or craft of attaching beads to one another by stringing them onto a thread or thin wire with a sewing or beading needle or sewing them to cloth. Beads are produced in a diverse range of materials, shapes, and sizes, and vary ...
, furniture
Furniture refers to movable objects intended to support various human activities such as seating (e.g., stools, chairs, and sofas), eating ( tables), storing items, eating and/or working with an item, and sleeping (e.g., beds and hammocks) ...
, sand painting
Sandpainting is the art of pouring coloured sands, and powdered pigments from minerals or crystals, or pigments from other natural or synthetic sources onto a surface to make a fixed or unfixed sand painting. Unfixed sand paintings have a long es ...
s, knot
A knot is an intentional complication in cordage which may be practical or decorative, or both. Practical knots are classified by function, including hitches, bends, loop knots, and splices: a ''hitch'' fastens a rope to another object; a ...
work, masks
A mask is an object normally worn on the face, typically for protection, disguise, performance, or entertainment and often they have been employed for rituals and rights. Masks have been used since antiquity for both ceremonial and pract ...
, and musical instruments
A musical instrument is a device created or adapted to make musical sounds. In principle, any object that produces sound can be considered a musical instrument—it is through purpose that the object becomes a musical instrument. A person who pl ...
. Symmetries are central to the art of M.C. Escher
Maurits Cornelis Escher (; 17 June 1898 – 27 March 1972) was a Dutch graphic artist who made Mathematics and art, mathematically inspired woodcuts, lithography, lithographs, and mezzotints.
Despite wide popular interest, Escher was for ...
and the many applications of tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of ...
in art and craft forms such as wallpaper
Wallpaper is a material used in interior decoration to decorate the interior walls of domestic and public buildings. It is usually sold in rolls and is applied onto a wall using wallpaper paste. Wallpapers can come plain as "lining paper" (so ...
, ceramic tilework such as in Islamic geometric decoration, batik
Batik is an Indonesian technique of wax-resist dyeing applied to the whole cloth. This technique originated from the island of Java, Indonesia. Batik is made either by drawing dots and lines of the resist with a spouted tool called a ''ca ...
, ikat
''Ikat'' (in Indonesian languages means "bind") is a dyeing technique originating from Indonesia used to pattern textiles that employs resist dyeing on the yarns prior to dyeing and weaving the fabric.
In ''ikat'', the resist is formed by b ...
, carpet-making, and many kinds of textile
Textile is an Hyponymy and hypernymy, umbrella term that includes various Fiber, fiber-based materials, including fibers, yarns, Staple (textiles)#Filament fiber, filaments, Thread (yarn), threads, different #Fabric, fabric types, etc. At f ...
and embroidery
Embroidery is the craft of decorating fabric or other materials using a needle to apply thread or yarn. Embroidery may also incorporate other materials such as pearls, beads, quills, and sequins. In modern days, embroidery is usually seen ...
patterns.
Symmetry is also used in designing logos. By creating a logo on a grid and using the theory of symmetry, designers can organize their work, create a symmetric or asymmetrical design, determine the space between letters, determine how much negative space is required in the design, and how to accentuate parts of the logo to make it stand out.
In music
music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspe ...
touches many aspects of the creation and perception of music.
Musical form
Symmetry has been used as a formal constraint by many composers, such as the arch (swell) form (ABCBA) used bySteve Reich
Stephen Michael Reich ( ; born October 3, 1936) is an American composer known for his contribution to the development of minimal music in the mid to late 1960s. Reich's work is marked by its use of repetitive figures, slow harmonic rhythm, ...
, Béla Bartók
Béla Viktor János Bartók (; ; 25 March 1881 – 26 September 1945) was a Hungarian composer, pianist, and ethnomusicologist. He is considered one of the most important composers of the 20th century; he and Franz Liszt are regarded as Hu ...
, and James Tenney
James Tenney (August 10, 1934 – August 24, 2006) was an American composer and music theorist. He made significant early musical contributions to plunderphonics, sound synthesis, algorithmic composition, process music, spectral music, microto ...
. In classical music, Bach used the symmetry concepts of permutation and invariance.
Pitch structures
Symmetry is also an important consideration in the formation of scales andchords
Chord may refer to:
* Chord (music), an aggregate of musical pitches sounded simultaneously
** Guitar chord a chord played on a guitar, which has a particular tuning
* Chord (geometry), a line segment joining two points on a curve
* Chord ( ...
, traditional or tonal music being made up of non-symmetrical groups of pitches, such as the diatonic scale
In music theory, a diatonic scale is any heptatonic scale that includes five whole steps (whole tones) and two half steps (semitones) in each octave, in which the two half steps are separated from each other by either two or three whole st ...
or the major chord
In music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the " rudiments", that are needed to understan ...
. Symmetrical scales or chords, such as the whole tone scale
In music, a whole-tone scale is a scale in which each note is separated from its neighbors by the interval of a whole tone. In twelve-tone equal temperament, there are only two complementary whole-tone scales, both six-note or '' hexatonic' ...
, augmented chord
Augment or augmentation may refer to:
Language
* Augment (Indo-European), a syllable added to the beginning of the word in certain Indo-European languages
*Augment (Bantu languages), a morpheme that is prefixed to the noun class prefix of nouns ...
, or diminished seventh chord
A seventh chord is a chord consisting of a triad plus a note forming an interval of a seventh above the chord's root. When not otherwise specified, a "seventh chord" usually means a dominant seventh chord: a major triad together with a mi ...
(diminished-diminished seventh), are said to lack direction or a sense of forward motion, are ambiguous
Ambiguity is the type of meaning in which a phrase, statement or resolution is not explicitly defined, making several interpretations plausible. A common aspect of ambiguity is uncertainty. It is thus an attribute of any idea or statement ...
as to the key or tonal center, and have a less specific diatonic functionality
In music, function (also referred to as harmonic function) is a term used to denote the relationship of a chord"Function", unsigned article, ''Grove Music Online'', . or a scale degree to a tonal centre. Two main theories of tonal functions exis ...
. However, composers such as Alban Berg
Alban Maria Johannes Berg ( , ; 9 February 1885 – 24 December 1935) was an Austrian composer of the Second Viennese School. His compositional style combined Romantic lyricism with the twelve-tone technique. Although he left a relatively sm ...
, Béla Bartók
Béla Viktor János Bartók (; ; 25 March 1881 – 26 September 1945) was a Hungarian composer, pianist, and ethnomusicologist. He is considered one of the most important composers of the 20th century; he and Franz Liszt are regarded as Hu ...
, and George Perle
George Perle (6 May 1915 – 23 January 2009) was an American composer and music theorist. As a composer, his music was largely atonal, using methods similar to the twelve-tone technique of the Second Viennese School. This serialist style, and ...
have used axes of symmetry and/or interval cycle In music, an interval cycle is a collection of pitch classes created from a sequence of the same interval class.Whittall, Arnold. 2008. ''The Cambridge Introduction to Serialism'', p. 273-74. New York: Cambridge University Press. (pbk). In other ...
s in an analogous way to keys
Key or The Key may refer to:
Common meanings
* Key (cryptography), a piece of information that controls the operation of a cryptography algorithm
* Key (lock), device used to control access to places or facilities restricted by a lock
* Key (m ...
or non- tonal tonal center
Center or centre may refer to:
Mathematics
*Center (geometry), the middle of an object
* Center (algebra), used in various contexts
** Center (group theory)
** Center (ring theory)
* Graph center, the set of all vertices of minimum eccentrici ...
s. George Perle explains "C–E, D–F♯, ndEb–G, are different instances of the same interval … the other kind of identity. … has to do with axes of symmetry. C–E belongs to a family of symmetrically related dyads as follows:"
Thus in addition to being part of the interval-4 family, C–E is also a part of the sum-4 family (with C equal to 0).
Interval cycles are symmetrical and thus non-diatonic. However, a seven pitch segment of C5 (the cycle of fifths, which are enharmonic
In modern musical notation and tuning, an enharmonic equivalent is a note, interval, or key signature that is equivalent to some other note, interval, or key signature but "spelled", or named differently. The enharmonic spelling of a writte ...
with the cycle of fourths) will produce the diatonic major scale. Cyclic tonal progressions in the works of Romantic composers such as Gustav Mahler
Gustav Mahler (; 7 July 1860 – 18 May 1911) was an Austro-Bohemian Romantic composer, and one of the leading conductors of his generation. As a composer he acted as a bridge between the 19th-century Austro-German tradition and the modernism ...
and Richard Wagner
Wilhelm Richard Wagner ( ; ; 22 May 181313 February 1883) was a German composer, theatre director, polemicist, and conductor who is chiefly known for his operas (or, as some of his mature works were later known, "music dramas"). Unlike most op ...
form a link with the cyclic pitch successions in the atonal music of Modernists such as Bartók, Alexander Scriabin
Alexander Nikolayevich Scriabin (; russian: Александр Николаевич Скрябин ; – ) was a Russian composer and virtuoso pianist. Before 1903, Scriabin was greatly influenced by the music of Frédéric Chopin and composed ...
, Edgard Varèse
Edgard Victor Achille Charles Varèse (; also spelled Edgar; December 22, 1883 – November 6, 1965) was a French-born composer who spent the greater part of his career in the United States. Varèse's music emphasizes timbre and rhythm; he coine ...
, and the Vienna school. At the same time, these progressions signal the end of tonality.
The first extended composition consistently based on symmetrical pitch relations was probably Alban Berg's ''Quartet'', Op. 3 (1910).
Equivalency
Tone row
In music, a tone row or note row (german: Reihe or '), also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets ...
s or pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
sets which are invariant under retrograde are horizontally symmetrical, under inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
vertically. See also Asymmetric rhythm
In music, the terms ''additive'' and ''divisive'' are used to distinguish two types of both rhythm and meter:
* A divisive (or, alternately, multiplicative) rhythm is a rhythm in which a larger period of time is divided into smaller rhythmic unit ...
.
In aesthetics
The relationship of symmetry toaesthetics
Aesthetics, or esthetics, is a branch of philosophy that deals with the nature of beauty and taste, as well as the philosophy of art (its own area of philosophy that comes out of aesthetics). It examines aesthetic values, often expressed t ...
is complex. Humans find bilateral symmetry
Symmetry in biology refers to the symmetry observed in organisms, including plants, animals, fungi, and bacteria. External symmetry can be easily seen by just looking at an organism. For example, take the face of a human being which has a ...
in faces physically attractive; it indicates health and genetic fitness.Jones, B. C., Little, A. C., Tiddeman, B. P., Burt, D. M., & Perrett, D. I. (2001). Facial symmetry and judgements of apparent health Support for a “‘ good genes ’” explanation of the attractiveness – symmetry relationship, 22, 417–429. Opposed to this is the tendency for excessive symmetry to be perceived as boring or uninteresting. Rudolf Arnheim suggested that people prefer shapes that have some symmetry, and enough complexity to make them interesting.
In literature
Symmetry can be found in various forms inliterature
Literature is any collection of Writing, written work, but it is also used more narrowly for writings specifically considered to be an art form, especially prose fiction, drama, and poetry. In recent centuries, the definition has expanded to ...
, a simple example being the palindrome
A palindrome is a word, number, phrase, or other sequence of symbols that reads the same backwards as forwards, such as the words ''madam'' or ''racecar'', the date and time ''11/11/11 11:11,'' and the sentence: "A man, a plan, a canal – Pana ...
where a brief text reads the same forwards or backwards. Stories may have a symmetrical structure, such as the rise and fall pattern of ''Beowulf
''Beowulf'' (; ang, Bēowulf ) is an Old English epic poem in the tradition of Germanic heroic legend consisting of 3,182 alliterative lines. It is one of the most important and most often translated works of Old English literature. ...
''.
See also
*Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphis ...
*Burnside's lemma
Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy–Frobenius lemma, the orbit-counting theorem, or the Lemma that is not Burnside's, is a result in group theory that is often useful in taking account of symmetry when ...
*Chirality
Chirality is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is distinguishable from ...
*Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power ser ...
*Fixed points of isometry groups in Euclidean space A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space.
For an object, any unique centre and, more ...
– center of symmetry
*Isotropy
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describ ...
*Palindrome
A palindrome is a word, number, phrase, or other sequence of symbols that reads the same backwards as forwards, such as the words ''madam'' or ''racecar'', the date and time ''11/11/11 11:11,'' and the sentence: "A man, a plan, a canal – Pana ...
*Spacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems. Spacetime symmetries are used in the study of exact ...
*Spontaneous symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or ...
*Symmetry-breaking constraints In the field of mathematics called combinatorial optimization, the method of symmetry-breaking constraints can be used to take advantage of symmetries in many constraint satisfaction and optimization problems, by adding constraints that eliminate sy ...
*Symmetric relation
A symmetric relation is a type of binary relation. An example is the relation "is equal to", because if ''a'' = ''b'' is true then ''b'' = ''a'' is also true. Formally, a binary relation ''R'' over a set ''X'' is symmetric if:
:\forall a, b \in X ...
* Symmetries of polyiamonds
* Symmetries of polyominoes
*Symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
*Wallpaper group
A wallpaper is a mathematical object covering a whole Euclidean plane by repeating a motif indefinitely, in manner that certain isometries keep the drawing unchanged. To a given wallpaper there corresponds a group of such congruent transformati ...
Notes
References
Further reading
* ''The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry'',Mario Livio
Mario Livio (born June 19, 1945) is an Israeli-American astrophysicist and an author of works that popularize science and mathematics. For 24 years (1991-2015) he was an astrophysicist at the Space Telescope Science Institute, which operates ...
, Souvenir Press
Ernest Hecht (21 September 1929 – 13 February 2018)Katherine Cowdrey"'Wise and witty' Ernest Hecht dies, aged 88" ''The Bookseller'', 13 February 2018. was a British publisher, producer, and philanthropist. In 1951, he founded Souvenir Press L ...
2006,
External links
International Symmetry Association (ISA)
Symmetry
BBC Radio 4 discussion with Fay Dowker, Marcus du Sautoy & Ian Stewart (''In Our Time'', Apr. 19, 2007) {{Patterns in nature Geometry Theoretical physics Artistic techniques Aesthetics