



A sundial is a
horological device that tells the time of
day (referred to as
civil time in modern usage) when direct
sunlight
Sunlight is a portion of the electromagnetic radiation given off by the Sun, in particular infrared, visible, and ultraviolet light. On Earth, sunlight is scattered and filtered through Earth's atmosphere, and is obvious as daylight when ...
shines by the
apparent position of the
Sun in the
sky. In the narrowest sense of the word, it consists of a flat plate (the ''dial'') and a
gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields.
History
A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the ...
, which casts a
shadow
A shadow is a dark area where light from a light source is blocked by an opaque object. It occupies all of the three-dimensional volume behind an object with light in front of it. The cross section of a shadow is a two- dimensional silhouett ...
onto the dial. As the Sun
appears to move through the sky, the shadow aligns with different hour-lines, which are marked on the dial to indicate the time of day. The ''style'' is the time-telling edge of the gnomon, though a single point or ''nodus'' may be used. The gnomon casts a broad shadow; the shadow of the style shows the time. The gnomon may be a rod, wire, or elaborately decorated metal casting. The style must be
parallel to the axis of the
Earth's rotation for the sundial to be accurate throughout the year. The style's angle from horizontal is equal to the sundial's geographical
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
.
The term ''sundial'' can refer to any device that uses the Sun's
altitude
Altitude or height (also sometimes known as depth) is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The exact definition and reference datum varies according to the context ...
or
azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north.
Mathematical ...
(or both) to show the time. Sundials are valued as decorative objects,
metaphor
A metaphor is a figure of speech that, for rhetorical effect, directly refers to one thing by mentioning another. It may provide (or obscure) clarity or identify hidden similarities between two different ideas. Metaphors are often compared wi ...
s, and objects of intrigue and mathematical study.
The passing of time can be observed by placing a stick in the sand or a nail in a board and placing markers at the edge of a shadow or outlining a shadow at intervals. It is common for inexpensive, mass-produced decorative sundials to have incorrectly aligned gnomons, shadow lengths, and hour-lines, which cannot be adjusted to tell correct time.
Introduction
There are several different types of sundials. Some sundials use a shadow or the edge of a shadow while others use a line or spot of light to indicate the time.
The shadow-casting object, known as a ''gnomon'', may be a long thin rod or other object with a sharp tip or a straight edge. Sundials employ many types of gnomon. The gnomon may be fixed or moved according to the season. It may be oriented vertically, horizontally, aligned with the Earth's axis, or oriented in an altogether different direction determined by mathematics.
Given that sundials use light to indicate time, a line of light may be formed by allowing the Sun's rays through a thin slit or focusing them through a
cylindrical lens. A spot of light may be formed by allowing the Sun's rays to pass through a small hole, window,
oculus Oculus (a term from Latin ''oculus'', meaning 'eye'), may refer to the following
Architecture
* Oculus (architecture), a circular opening in the centre of a dome or in a wall
Arts, entertainment, and media
* ''Oculus'' (film), a 2013 American s ...
, or by reflecting them from a small circular mirror. A spot of light can be as small as a
pinhole in a solargraph or as large as the oculus in the Pantheon.
Sundials also may use many types of surfaces to receive the light or shadow.
Planes
Plane(s) most often refers to:
* Aero- or airplane, a powered, fixed-wing aircraft
* Plane (geometry), a flat, 2-dimensional surface
Plane or planes may also refer to:
Biology
* Plane (tree) or ''Platanus'', wetland native plant
* ''Planes' ...
are the most common surface, but partial
sphere
A sphere () is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the c ...
s,
cylinders,
cones and other shapes have been used for greater accuracy or beauty.
Sundials differ in their portability and their need for orientation. The installation of many dials requires knowing the local
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
, the precise vertical direction (e.g., by a level or plumb-bob), and the direction to
true North. Portable dials are self-aligning: for example, it may have two dials that operate on different principles, such as a horizontal and
analemmatic dial, mounted together on one plate. In these designs, their times agree only when the plate is aligned properly.
Sundials may indicate the
local solar time only. To obtain the national clock time, three corrections are required:
# The orbit of the Earth is not perfectly circular and its rotational axis is not perpendicular to its orbit. The sundial's indicated solar time thus varies from clock time by small amounts that change throughout the year. This correction—which may be as great as 16 minutes, 33 seconds—is described by the
equation of time. A sophisticated sundial, with a curved style or hour lines, may incorporate this correction. The more usual simpler sundials sometimes have a small plaque that gives the offsets at various times of the year.
# The solar time must be corrected for the
longitude
Longitude (, ) is a geographic coordinate that specifies the east– west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek let ...
of the sundial relative to the longitude of the official time zone. For example, an uncorrected sundial located ''west'' of
Greenwich, England but within the same time-zone, shows an ''earlier'' time than the official time. It may show "11:45" at official noon, and will show "noon" after the official noon. This correction can easily be made by rotating the hour-lines by a constant angle equal to the difference in longitudes, which makes this a commonly possible design option.
# To adjust for
daylight saving time
Daylight saving time (DST), also referred to as daylight savings time or simply daylight time (United States, Canada, and Australia), and summer time (United Kingdom, European Union, and others), is the practice of advancing clocks (typicall ...
, if applicable, the solar time must additionally be shifted for the official difference (usually one hour). This is also a correction that can be done on the dial, i.e. by numbering the hour-lines with two sets of numbers, or even by swapping the numbering in some designs. More often this is simply ignored, or mentioned on the plaque with the other corrections, if there is one.
Apparent motion of the Sun

The principles of sundials are understood most easily from the
Sun's apparent motion. The Earth rotates on its axis, and revolves in an elliptical orbit around the Sun. An excellent approximation assumes that the Sun revolves around a stationary Earth on the
celestial sphere, which rotates every 24 hours about its celestial axis. The celestial axis is the line connecting the
celestial poles. Since the celestial axis is aligned with the axis about which the Earth rotates, the angle of the axis with the local horizontal is the local geographical
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
.
Unlike the
fixed stars, the Sun changes its position on the celestial sphere, being (in the northern hemisphere) at a positive
declination in spring and summer, and at a negative declination in autumn and winter, and having exactly zero declination (i.e., being on the
celestial equator) at the
equinoxes. The Sun's
celestial longitude also varies, changing by one complete revolution per year. The path of the Sun on the celestial sphere is called the
ecliptic. The ecliptic passes through the twelve constellations of the
zodiac
The zodiac is a belt-shaped region of the sky that extends approximately 8° north or south (as measured in celestial latitude) of the ecliptic, the apparent path of the Sun across the celestial sphere over the course of the year. The pa ...
in the course of a year.

This model of the Sun's motion helps to understand sundials. If the shadow-casting gnomon is aligned with the
celestial poles, its shadow will revolve at a constant rate, and this rotation will not change with the seasons. This is the most common design. In such cases, the same hour lines may be used throughout the year. The hour-lines will be spaced uniformly if the surface receiving the shadow is either perpendicular (as in the equatorial sundial) or circular about the gnomon (as in the
armillary sphere).
In other cases, the hour-lines are not spaced evenly, even though the shadow rotates uniformly. If the gnomon is ''not'' aligned with the celestial poles, even its shadow will not rotate uniformly, and the hour lines must be corrected accordingly. The rays of light that graze the tip of a gnomon, or which pass through a small hole, or reflect from a small mirror, trace out a
cone aligned with the celestial poles. The corresponding light-spot or shadow-tip, if it falls onto a flat surface, will trace out a
conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a ...
, such as a
hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
,
ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
or (at the North or South Poles) a
circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
.
This conic section is the intersection of the cone of light rays with the flat surface. This cone and its conic section change with the seasons, as the Sun's declination changes; hence, sundials that follow the motion of such light-spots or shadow-tips often have different hour-lines for different times of the year. This is seen in shepherd's dials, sundial rings, and vertical gnomons such as obelisks. Alternatively, sundials may change the angle or position (or both) of the gnomon relative to the hour lines, as in the analemmatic dial or the Lambert dial.
History


The earliest sundials known from the archaeological record are shadow clocks (1500
BC or
BCE) from ancient
Egyptian astronomy
Egyptian astronomy began in prehistoric times, in the Predynastic Period. In the 5th millennium BCE, the stone circles at Nabta Playa may have made use of astronomical alignments. By the time the historical Dynastic Period began in the 3rd m ...
and
Babylonian astronomy
Babylonian astronomy was the study or recording of celestial objects during the early history of Mesopotamia.
Babylonian astronomy seemed to have focused on a select group of stars and constellations known as Ziqpu stars. These constellation ...
. Presumably, humans were telling time from shadow-lengths at an even earlier date, but this is hard to verify. In roughly 700 BC, the
Old Testament
The Old Testament (often abbreviated OT) is the first division of the Christian biblical canon, which is based primarily upon the 24 books of the Hebrew Bible or Tanakh, a collection of ancient religious Hebrew writings by the Israelites. The ...
describes a sundial—the "dial of Ahaz" mentioned in and . By 240 BC Eratosthenes had estimated the
circumference
In geometry, the circumference (from Latin ''circumferens'', meaning "carrying around") is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out ...
of the world using an obelisk and a water well and a few centuries later Ptolemy had charted the latitude of cities using the angle of the sun. The people of
Kush
Kush or Cush may refer to:
Bible
* Cush (Bible), two people and one or more places in the Hebrew Bible
Places
* Kush (mountain), a mountain near Kalat, Pakistan Balochistan
* Kush (satrapy), a satrapy of the Achaemenid Empire
* Hindu Kush, a ...
created sun dials through geometry. The Roman writer
Vitruvius
Vitruvius (; c. 80–70 BC – after c. 15 BC) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work entitled '' De architectura''. He originated the idea that all buildings should have three attribut ...
lists dials and shadow clocks known at that time in his ''
De architectura
(''On architecture'', published as ''Ten Books on Architecture'') is a treatise on architecture written by the Roman architect and military engineer Marcus Vitruvius Pollio and dedicated to his patron, the emperor Caesar Augustus, as a guide ...
''. The Tower of Winds constructed in Athens included sundial and a water clock for telling time. A
canonical sundial is one that indicates the canonical hours of liturgical acts. Such sundials were used from the 7th to the 14th centuries by the members of religious communities. The Italian astronomer
Giovanni Padovani
Giovanni Padovani (or Paduani) (b. c. 1512) was an Italian mathematician and astronomer. He lived in Verona and was a student of Pietro Pitati. He published a number of esteemed treatises on various astronomical and mathematical subjects, the m ...
published a treatise on the sundial in 1570, in which he included instructions for the manufacture and laying out of mural (vertical) and horizontal sundials.
Giuseppe Biancani
Giuseppe Biancani, SJ (Latin: Josephus Blancanus) (1566–1624) was an Italian Jesuit astronomer, mathematician, and selenographer, after whom the crater Blancanus on the Moon is named. He was a native of Bologna.
Works
His ''Aristotelis ...
's ''Constructio instrumenti ad horologia solaria'' (c. 1620) discusses how to make a perfect sundial. They have been commonly used since the 16th century.
Functioning

In general, sundials indicate the time by casting a shadow or throwing light onto a surface known as a ''dial face'' or ''dial plate''. Although usually a flat plane, the dial face may also be the inner or outer surface of a sphere, cylinder, cone, helix, and various other shapes.
The time is indicated where a shadow or light falls on the dial face, which is usually inscribed with hour lines. Although usually straight, these hour lines may also be curved, depending on the design of the sundial (see below). In some designs, it is possible to determine the date of the year, or it may be required to know the date to find the correct time. In such cases, there may be multiple sets of hour lines for different months, or there may be mechanisms for setting/calculating the month. In addition to the hour lines, the dial face may offer other data—such as the horizon, the equator and the tropics—which are referred to collectively as the dial furniture.
The entire object that casts a shadow or light onto the dial face is known as the sundial's ''gnomon''.
However, it is usually only an edge of the gnomon (or another linear feature) that casts the shadow used to determine the time; this linear feature is known as the sundial's ''style''. The style is usually aligned parallel to the axis of the celestial sphere, and therefore is aligned with the local geographical meridian. In some sundial designs, only a point-like feature, such as the tip of the style, is used to determine the time and date; this point-like feature is known as the sundial's ''nodus''.
Some sundials use both a style and a nodus to determine the time and date.
The gnomon is usually fixed relative to the dial face, but not always; in some designs such as the analemmatic sundial, the style is moved according to the month. If the style is fixed, the line on the dial plate perpendicularly beneath the style is called the ''substyle'',
meaning "below the style". The angle the style makes with the plane of the dial plate is called the substyle height, an unusual use of the word ''height'' to mean an ''angle''. On many wall dials, the substyle is not the same as the noon line (see below). The angle on the dial plate between the noon line and the substyle is called the ''substyle distance'', an unusual use of the word ''distance'' to mean an ''angle''.
By tradition, many sundials have a
motto
A motto (derived from the Latin , 'mutter', by way of Italian , 'word' or 'sentence') is a sentence or phrase expressing a belief or purpose, or the general motivation or intention of an individual, family, social group, or organisation. M ...
. The motto is usually in the form of an
epigram: sometimes sombre reflections on the passing of time and the brevity of life, but equally often humorous witticisms of the dial maker. One such quip is, ''I am a sundial, and I make a botch, Of what is done much better by a watch.''
A dial is said to be ''equiangular'' if its hour-lines are straight and spaced equally. Most equiangular sundials have a fixed gnomon style aligned with the Earth's rotational axis, as well as a shadow-receiving surface that is symmetrical about that axis; examples include the equatorial dial, the equatorial bow, the armillary sphere, the cylindrical dial and the conical dial. However, other designs are equiangular, such as the Lambert dial, a version of the
analemmatic sundial with a moveable style.
In the Southern Hemisphere

A sundial at a particular
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
in one
hemisphere
Hemisphere refers to:
* A half of a sphere
As half of the Earth
* A hemisphere of Earth
** Northern Hemisphere
** Southern Hemisphere
** Eastern Hemisphere
** Western Hemisphere
** Land and water hemispheres
* A half of the (geocentric) celes ...
must be reversed for use at the opposite latitude in the other hemisphere.
A vertical direct south sundial in the
Northern Hemisphere
The Northern Hemisphere is the half of Earth that is north of the Equator. For other planets in the Solar System, north is defined as being in the same celestial hemisphere relative to the invariable plane of the solar system as Earth's Nort ...
becomes a vertical direct north sundial in the
Southern Hemisphere. To position a horizontal sundial correctly, one has to find true
North
North is one of the four compass points or cardinal directions. It is the opposite of south and is perpendicular to east and west. ''North'' is a noun, adjective, or adverb indicating direction or geography.
Etymology
The word ''north ...
or
South. The same process can be used to do both.
The gnomon, set to the correct latitude, has to point to the true South in the Southern hemisphere as in the Northern Hemisphere it has to point to the true North.
The hour numbers also run in opposite directions, so on a horizontal dial they run anticlockwise (US: counterclockwise) rather than clockwise.
Sundials which are designed to be used with their plates horizontal in one hemisphere can be used with their plates vertical at the complementary latitude in the other hemisphere. For example, the illustrated sundial in
Perth
Perth is the capital and largest city of the Australian state of Western Australia. It is the fourth most populous city in Australia and Oceania, with a population of 2.1 million (80% of the state) living in Greater Perth in 2020. Perth is ...
,
Australia
Australia, officially the Commonwealth of Australia, is a sovereign country comprising the mainland of the Australian continent, the island of Tasmania, and numerous smaller islands. With an area of , Australia is the largest country by ...
, which is at latitude 32 degrees South, would function properly if it were mounted on a south-facing vertical wall at latitude 58 (i.e. 90–32) degrees North, which is slightly further North than
Perth, Scotland
Perth (Scottish English, locally: ; gd, Peairt ) is a city in central Scotland, on the banks of the River Tay. It is the administrative centre of Perth and Kinross council area and the historic county town of Perthshire. It had a population o ...
. The surface of the wall in Scotland would be parallel with the horizontal ground in Australia (ignoring the difference of longitude), so the sundial would work identically on both surfaces. Correspondingly, the hour marks, which run counterclockwise on a horizontal sundial in the southern hemisphere, also do so on a vertical sundial in the northern hemisphere. (See the first two illustrations at the top of this article.) On horizontal northern-hemisphere sundials, and on vertical southern-hemisphere ones, the hour marks run clockwise.
Adjustments to calculate clock time from a sundial reading
The most common reason for a sundial to differ greatly from clock time is that the sundial has not been oriented correctly or its hour lines have not been drawn correctly. For example, most commercial sundials are designed as ''horizontal sundials'' as described above. To be accurate, such a sundial must have been designed for the local geographical latitude and its style must be parallel to the Earth's rotational axis; the style must be aligned with
true North and its ''height'' (its angle with the horizontal) must equal the local latitude. To adjust the style height, the sundial can often be tilted slightly "up" or "down" while maintaining the style's north-south alignment.
Summer (daylight saving) time correction
Some areas of the world practice
daylight saving time
Daylight saving time (DST), also referred to as daylight savings time or simply daylight time (United States, Canada, and Australia), and summer time (United Kingdom, European Union, and others), is the practice of advancing clocks (typicall ...
, which changes the official time, usually by one hour. This shift must be added to the sundial's time to make it agree with the official time.
Time-zone (longitude) correction
A standard
time zone covers roughly 15° of longitude, so any point within that zone which is not on the reference longitude (generally a multiple of 15°) will experience a difference from standard time that is equal to 4 minutes of time per degree. For illustration, sunsets and sunrises are at a much later "official" time at the western edge of a time-zone, compared to sunrise and sunset times at the eastern edge. If a sundial is located at, say, a longitude 5° west of the reference longitude, then its time will read 20 minutes slow, since the Sun appears to revolve around the Earth at 15° per hour. This is a constant correction throughout the year. For equiangular dials such as equatorial, spherical or Lambert dials, this correction can be made by rotating the dial surface by an angle equaling the difference in longitude, without changing the gnomon position or orientation. However, this method does not work for other dials, such as a horizontal dial; the correction must be applied by the viewer.
However, for political and practical reasons, time-zone boundaries have been skewed. At their most extreme, time zones can cause official noon, including daylight savings, to occur up to three hours early (in which case the Sun is actually on the
meridian at official clock time of 3 pm). This occurs in the far west of
Alaska
Alaska ( ; russian: Аляска, Alyaska; ale, Alax̂sxax̂; ; ems, Alas'kaaq; Yup'ik: ''Alaskaq''; tli, Anáaski) is a state located in the Western United States on the northwest extremity of North America. A semi-exclave of the U ...
,
China
China, officially the People's Republic of China (PRC), is a country in East Asia. It is the world's List of countries and dependencies by population, most populous country, with a Population of China, population exceeding 1.4 billion, slig ...
, and
Spain
, image_flag = Bandera de España.svg
, image_coat = Escudo de España (mazonado).svg
, national_motto = '' Plus ultra'' (Latin)(English: "Further Beyond")
, national_anthem = (English: "Royal March")
, ...
. For more details and examples, see
time zones
Time is the continued sequence of existence and events that occurs in an apparently irreversible succession from the past, through the present, into the future. It is a component quantity of various measurements used to sequence events, t ...
.
Equation of time correction

Although the Sun appears to rotate uniformly about the Earth, in reality this motion is not perfectly uniform. This is due to the
eccentricity of the Earth's orbit (the fact that the Earth's orbit about the Sun is not perfectly circular, but slightly
elliptical) and the tilt (obliquity) of the Earth's rotational axis relative to the plane of its orbit. Therefore, sundial time varies from
standard clock time. On four days of the year, the correction is effectively zero. However, on others, it can be as much as a quarter-hour early or late. The amount of correction is described by the
equation of time. This correction is equal worldwide: it does not depend on the local
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
or
longitude
Longitude (, ) is a geographic coordinate that specifies the east– west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek let ...
of the observer's position. It does, however, change over long periods of time, (centuries or more,)
because of slow variations in the Earth's orbital and rotational motions. Therefore, tables and graphs of the equation of time that were made centuries ago are now significantly incorrect. The reading of an old sundial should be corrected by applying the present-day equation of time, not one from the period when the dial was made.
In some sundials, the equation of time correction is provided as an informational plaque affixed to the sundial, for the observer to calculate. In more sophisticated sundials the equation can be incorporated automatically. For example, some equatorial bow sundials are supplied with a small wheel that sets the time of year; this wheel in turn rotates the equatorial bow, offsetting its time measurement. In other cases, the hour lines may be curved, or the equatorial bow may be shaped like a vase, which exploits the changing altitude of the sun over the year to effect the proper offset in time.
A ''heliochronometer'' is a precision sundial first devised in about 1763 by
Philipp Hahn and improved by Abbé Guyoux in about 1827.
[
]
It corrects
apparent solar time to
mean solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Two types of solar time are apparent solar time ( sundia ...
or another
standard time. Heliochronometers usually indicate the minutes to within 1 minute of
Universal Time
Universal Time (UT or UT1) is a time standard based on Earth's rotation. While originally it was mean solar time at 0° longitude, precise measurements of the Sun are difficult. Therefore, UT1 is computed from a measure of the Earth's angle wit ...
.

The
Sunquest sundial
The Sunquest Sundial is a sundial designed by Richard L. Schmoyer in the 1950s. Adjustable for latitude and longitude, the Sunquest's gnomon automatically corrects for the equation of time allowing it to tell clock time.
The Sunquest sundial util ...
, designed by Richard L. Schmoyer in the 1950s, uses an analemmic inspired gnomon to cast a shaft of light onto an equatorial time-scale crescent. Sunquest is adjustable for latitude and longitude, automatically correcting for the equation of time, rendering it "as accurate as most pocket watches". Similarly, in place of the shadow of a gnomon th
sundial at Miguel Hernández Universityuses the solar projection of a graph of the equation of time intersecting a time scale to display clock time directly.

An analemma may be added to many types of sundials to correct apparent solar time to
mean solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Two types of solar time are apparent solar time ( sundia ...
or another
standard time. These usually have hour lines shaped like "figure eights" (
analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same mean solar time, as that position varies over the course of a year. The diagram will resemble a figur ...
s) according to the
equation of time. This compensates for the slight eccentricity in the Earth's orbit and the tilt of the Earth's axis that causes up to a 15-minute variation from mean solar time. This is a type of dial furniture seen on more complicated horizontal and vertical dials.
Prior to the invention of accurate clocks, in the mid-17th Century, sundials were the only timepieces in common use, and were considered to tell the "right" time. The Equation of Time was not used. After the invention of good clocks, sundials were still considered to be correct, and clocks usually incorrect. The Equation of Time was used in the opposite direction from today, to apply a correction to the time shown by a clock to make it agree with sundial time. Some elaborate "
equation clock
An equation clock is a mechanical clock which includes a mechanism that simulates the equation of time, so that the user can read or calculate solar time, as would be shown by a sundial. The first accurate clocks, controlled by pendulums, were ...
s", such as one made by Joseph Williamson in 1720, incorporated mechanisms to do this correction automatically. (Williamson's clock may have been the first-ever device to use a
differential gear.) Only after about 1800 was uncorrected clock time considered to be "right", and sundial time usually "wrong", so the Equation of Time became used as it is today.
With fixed axial gnomon

The most commonly observed sundials are those in which the shadow-casting style is fixed in position and aligned with the Earth's rotational axis, being oriented with
true North and South, and making an angle with the horizontal equal to the geographical latitude. This axis is aligned with the
celestial poles, which is closely, but not perfectly, aligned with the
pole star Polaris
Polaris is a star in the northern circumpolar constellation of Ursa Minor. It is designated α Ursae Minoris ( Latinized to ''Alpha Ursae Minoris'') and is commonly called the North Star or Pole Star. With an apparent magnitude th ...
. For illustration, the celestial axis points vertically at the true
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's axis of rotation meets its surface. It is called the True North Pole to distinguish from the Ma ...
, where it points horizontally on the
equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also ...
. The world's largest axial gnomon sundial is the mast of the
Sundial Bridge at Turtle Bay
The Sundial Bridge (also known as the Sundial Bridge at Turtle Bay) is a cantilever spar cable-stayed bridge for bicycles and pedestrians that spans the Sacramento River in Redding, California, United States and forms a large sundial. It was d ...
in
Redding, California
Redding is the economic and cultural capital of the Shasta Cascade region of Northern California and the county seat of Shasta County. Redding lies along the Sacramento River, north of Sacramento, and south of California's northern border wi ...
. A formerly world's largest gnomon is at
Jaipur
Jaipur (; Hindi: ''Jayapura''), formerly Jeypore, is the capital and largest city of the Indian state of Rajasthan. , the city had a population of 3.1 million, making it the tenth most populous city in the country. Jaipur is also known a ...
, raised 26°55" above horizontal, reflecting the local latitude.
On any given day, the Sun appears to rotate uniformly about this axis, at about 15° per hour, making a full circuit (360°) in 24 hours. A linear gnomon aligned with this axis will cast a sheet of shadow (a half-plane) that, falling opposite to the Sun, likewise rotates about the celestial axis at 15° per hour. The shadow is seen by falling on a receiving surface that is usually flat, but which may be spherical, cylindrical, conical or of other shapes. If the shadow falls on a surface that is symmetrical about the celestial axis (as in an armillary sphere, or an equatorial dial), the surface-shadow likewise moves uniformly; the hour-lines on the sundial are equally spaced. However, if the receiving surface is not symmetrical (as in most horizontal sundials), the surface shadow generally moves non-uniformly and the hour-lines are not equally spaced; one exception is the Lambert dial described below.
Some types of sundials are designed with a fixed gnomon that is not aligned with the celestial poles like a vertical obelisk. Such sundials are covered below under the section, "Nodus-based sundials".
Empirical hour-line marking
The formulas shown in the paragraphs below allow the positions of the hour-lines to be calculated for various types of sundial. In some cases, the calculations are simple; in others they are extremely complicated. There is an alternative, simple method of finding the positions of the hour-lines which can be used for many types of sundial, and saves a lot of work in cases where the calculations are complex. This is an empirical procedure in which the position of the shadow of the gnomon of a real sundial is marked at hourly intervals. The
equation of time must be taken into account to ensure that the positions of the hour-lines are independent of the time of year when they are marked. An easy way to do this is to set a clock or watch so it shows "sundial time" which is
standard time, plus the equation of time on the day in question. The hour-lines on the sundial are marked to show the positions of the shadow of the style when this clock shows whole numbers of hours, and are labelled with these numbers of hours. For example, when the clock reads 5:00, the shadow of the style is marked, and labelled "5" (or "V" in
Roman numerals
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, ...
). If the hour-lines are not all marked in a single day, the clock must be adjusted every day or two to take account of the variation of the equation of time.
Equatorial sundials


The distinguishing characteristic of the ''equatorial dial'' (also called the ''equinoctial dial'') is the planar surface that receives the shadow, which is exactly perpendicular to the gnomon's style. This plane is called equatorial, because it is parallel to the equator of the Earth and of the celestial sphere. If the gnomon is fixed and aligned with the Earth's rotational axis, the sun's apparent rotation about the Earth casts a uniformly rotating sheet of shadow from the gnomon; this produces a uniformly rotating line of shadow on the equatorial plane. Since the Earth rotates 360° in 24 hours, the hour-lines on an equatorial dial are all spaced 15° apart (360/24).
:
The uniformity of their spacing makes this type of sundial easy to construct. If the dial plate material is opaque, both sides of the equatorial dial must be marked, since the shadow will be cast from below in winter and from above in summer. With translucent dial plates (e.g. glass) the hour angles need only be marked on the sun-facing side, although the hour numberings (if used) need be made on both sides of the dial, owing to the differing hour schema on the sun-facing and sun-backing sides.
Another major advantage of this dial is that equation of time (EoT) and daylight saving time (DST) corrections can be made by simply rotating the dial plate by the appropriate angle each day. This is because the hour angles are equally spaced around the dial. For this reason, an equatorial dial is often a useful choice when the dial is for public display and it is desirable to have it show the true local time to reasonable accuracy. The EoT correction is made via the relation
:
Near the
equinoxes in spring and autumn, the sun moves on a circle that is nearly the same as the equatorial plane; hence, no clear shadow is produced on the equatorial dial at those times of year, a drawback of the design.
A ''nodus'' is sometimes added to equatorial sundials, which allows the sundial to tell the time of year. On any given day, the shadow of the nodus moves on a circle on the equatorial plane, and the radius of the circle measures the
declination of the sun. The ends of the gnomon bar may be used as the nodus, or some feature along its length. An ancient variant of the equatorial sundial has only a nodus (no style) and the concentric circular hour-lines are arranged to resemble a spider-web.
Horizontal sundials

In the ''horizontal sundial'' (also called a ''garden sundial''), the plane that receives the shadow is aligned horizontally, rather than being perpendicular to the style as in the equatorial dial. Hence, the line of shadow does not rotate uniformly on the dial face; rather, the hour lines are spaced according to the rule.
:
Or in other terms:
:
where L is the sundial's geographical
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
(and the angle the gnomon makes with the dial plate),
is the angle between a given hour-line and the noon hour-line (which always points towards
true North) on the plane, and ''t'' is the number of hours before or after noon. For example, the angle
of the 3pm hour-line would equal the
arctangent
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Spe ...
of
sin L, since tan 45° = 1. When L equals 90° (at the
North Pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's axis of rotation meets its surface. It is called the True North Pole to distinguish from the Ma ...
), the horizontal sundial becomes an equatorial sundial; the style points straight up (vertically), and the horizontal plane is aligned with the equatorial plane; the hour-line formula becomes
= 15° × t, as for an equatorial dial. A horizontal sundial at the Earth's
equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can also ...
, where L equals 0°, would require a (raised) horizontal style and would be an example of a polar sundial (see below).


The chief advantages of the horizontal sundial are that it is easy to read, and the sunlight lights the face throughout the year. All the hour-lines intersect at the point where the gnomon's style crosses the horizontal plane. Since the style is aligned with the Earth's rotational axis, the style points
true North and its angle with the horizontal equals the sundial's geographical latitude L. A sundial designed for one
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
can be adjusted for use at another latitude by tilting its base upwards or downwards by an angle equal to the difference in latitude. For example, a sundial designed for a latitude of 40° can be used at a latitude of 45°, if the sundial plane is tilted upwards by 5°, thus aligning the style with the Earth's rotational axis.
Many ornamental sundials are designed to be used at 45 degrees north. Some mass-produced garden sundials fail to correctly calculate the ''hourlines'' and so can never be corrected. A local standard
time zone is nominally 15 degrees wide, but may be modified to follow geographic or political boundaries. A sundial can be rotated around its style (which must remain pointed at the celestial pole) to adjust to the local time zone. In most cases, a rotation in the range of 7.5 degrees east to 23 degrees west suffices. This will introduce error in sundials that do not have equal hour angles. To correct for
daylight saving time
Daylight saving time (DST), also referred to as daylight savings time or simply daylight time (United States, Canada, and Australia), and summer time (United Kingdom, European Union, and others), is the practice of advancing clocks (typicall ...
, a face needs two sets of numerals or a correction table. An informal standard is to have numerals in hot colors for summer, and in cool colors for winter. Since the hour angles are not evenly spaced, the equation of time corrections cannot be made via rotating the dial plate about the gnomon axis. These types of dials usually have an equation of time correction tabulation engraved on their pedestals or close by. Horizontal dials are commonly seen in gardens, churchyards and in public areas.
Vertical sundials

In the common ''vertical dial'', the shadow-receiving plane is aligned vertically; as usual, the gnomon's style is aligned with the Earth's axis of rotation. As in the horizontal dial, the line of shadow does not move uniformly on the face; the sundial is not ''equiangular''. If the face of the vertical dial points directly south, the angle of the hour-lines is instead described by the formula
:
where L is the sundial's geographical
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
,
is the angle between a given hour-line and the noon hour-line (which always points due north) on the plane, and ''t'' is the number of hours before or after noon. For example, the angle
of the 3pm hour-line would equal the
arctangent
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Spe ...
of
cos
Cos, COS, CoS, coS or Cos. may refer to:
Mathematics, science and technology
* Carbonyl sulfide
* Class of service (CoS or COS), a network header field defined by the IEEE 802.1p task group
* Class of service (COS), a parameter in telephone syst ...
L, since tan 45° = 1. The shadow moves ''counter-clockwise'' on a south-facing vertical dial, whereas it runs clockwise on horizontal and equatorial north-facing dials.
Dials with faces perpendicular to the ground and which face directly South, North, East, or West are called ''vertical direct dials''. It is widely believed, and stated in respectable publications, that a vertical dial cannot receive more than twelve hours of sunlight a day, no matter how many hours of daylight there are. However, there is an exception. Vertical sundials in the tropics which face the nearer pole (e.g. north facing in the zone between the Equator and the Tropic of Cancer) can actually receive sunlight for more than 12 hours from sunrise to sunset for a short period around the time of the summer solstice. For example, at latitude 20 degrees North, on June 21, the sun shines on a north-facing vertical wall for 13 hours, 21 minutes.
Vertical sundials which do ''not'' face directly South (in the northern hemisphere) may receive significantly less than twelve hours of sunlight per day, depending on the direction they do face, and on the time of year. For example, a vertical dial that faces due East can tell time only in the morning hours; in the afternoon, the sun does not shine on its face. Vertical dials that face due East or West are ''polar dials'', which will be described below. Vertical dials that face North are uncommon, because they tell time only during the spring and summer, and do not show the midday hours except in tropical latitudes (and even there, only around midsummer). For non-direct vertical dials—those that face in non-cardinal directions—the mathematics of arranging the style and the hour-lines becomes more complicated; it may be easier to mark the hour lines by observation, but the placement of the style, at least, must be calculated first; such dials are said to be ''declining dials''.

Vertical dials are commonly mounted on the walls of buildings, such as town-halls,
cupola
In architecture, a cupola () is a relatively small, most often dome-like, tall structure on top of a building. Often used to provide a lookout or to admit light and air, it usually crowns a larger roof or dome.
The word derives, via Italian, f ...
s and church-towers, where they are easy to see from far away. In some cases, vertical dials are placed on all four sides of a rectangular tower, providing the time throughout the day. The face may be painted on the wall, or displayed in inlaid stone; the gnomon is often a single metal bar, or a tripod of metal bars for rigidity. If the wall of the building faces ''toward'' the South, but does not face due South, the gnomon will not lie along the noon line, and the hour lines must be corrected. Since the gnomon's style must be parallel to the Earth's axis, it always "points"
true North and its angle with the horizontal will equal the sundial's geographical latitude; on a direct south dial, its angle with the vertical face of the dial will equal the
colatitude
In a spherical coordinate system, a colatitude is the complementary angle of a given latitude, i.e. the difference between a right angle and the latitude. Here Southern latitudes are defined to be negative, and as a result the colatitude is a no ...
, or 90° minus the latitude.
Polar dials

In ''polar dials'', the shadow-receiving plane is aligned ''parallel'' to the gnomon-style.
Thus, the shadow slides sideways over the surface, moving perpendicularly to itself as the Sun rotates about the style. As with the gnomon, the hour-lines are all aligned with the Earth's rotational axis. When the Sun's rays are nearly parallel to the plane, the shadow moves very quickly and the hour lines are spaced far apart. The direct East- and West-facing dials are examples of a polar dial. However, the face of a polar dial need not be vertical; it need only be parallel to the gnomon. Thus, a plane inclined at the angle of latitude (relative to horizontal) under the similarly inclined gnomon will be a polar dial. The perpendicular spacing ''X'' of the hour-lines in the plane is described by the formula
:
where ''H'' is the height of the style above the plane, and ''t'' is the time (in hours) before or after the center-time for the polar dial. The center time is the time when the style's shadow falls directly down on the plane; for an East-facing dial, the center time will be 6am, for a West-facing dial, this will be 6pm, and for the inclined dial described above, it will be noon. When ''t'' approaches ±6 hours away from the center time, the spacing ''X'' diverges to
+∞; this occurs when the Sun's rays become parallel to the plane.
Vertical declining dials

A ''declining dial'' is any non-horizontal, planar dial that does not face in a cardinal direction, such as (true)
North
North is one of the four compass points or cardinal directions. It is the opposite of south and is perpendicular to east and west. ''North'' is a noun, adjective, or adverb indicating direction or geography.
Etymology
The word ''north ...
,
South,
East or
West. As usual, the gnomon's style is aligned with the Earth's rotational axis, but the hour-lines are not symmetrical about the noon hour-line. For a vertical dial, the angle
between the noon hour-line and another hour-line is given by the formula below. Note that
is defined positive in the clockwise sense w.r.t. the upper vertical hour angle; and that its conversion to the equivalent solar hour requires careful consideration of which quadrant of the sundial that it belongs in.
:
where
is the sundial's geographical
latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
; ''t'' is the time before or after noon;
is the angle of declination from true
south, defined as positive when east of south; and
is a switch integer for the dial orientation. A partly south-facing dial has an
value of + 1; those partly north-facing, a value of -1. When such a dial faces South (
), this formula reduces to the formula given above for vertical south-facing dials, i.e.
:
When a sundial is not aligned with a cardinal direction, the substyle of its gnomon is not aligned with the noon hour-line. The angle
between the substyle and the noon hour-line is given by the formula
:
If a vertical sundial faces true South or North (
or
, respectively), the angle
and the substyle is aligned with the noon hour-line.
The height of the gnomon, that is the angle the style makes to the plate,
, is given by :
:
Reclining dials
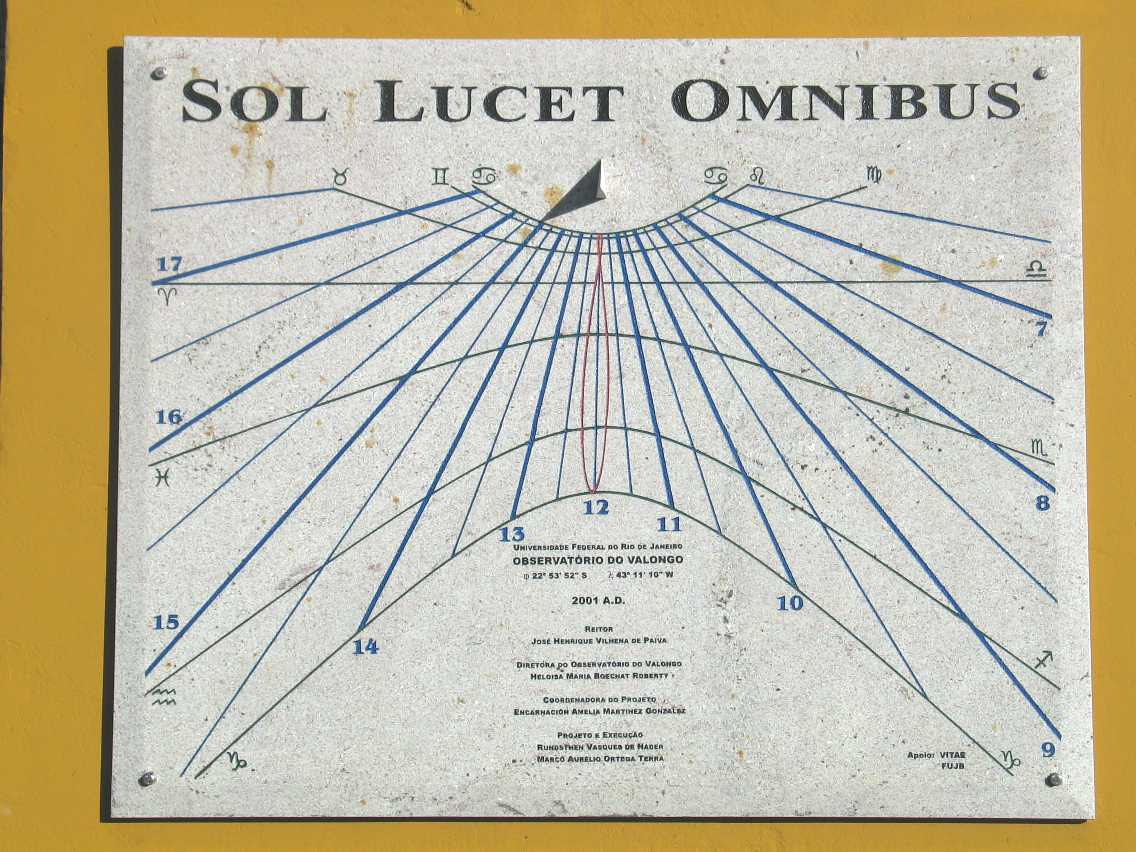
The sundials described above have gnomons that are aligned with the Earth's rotational axis and cast their shadow onto a plane. If the plane is neither vertical nor horizontal nor equatorial, the sundial is said to be ''reclining'' or ''inclining''. Such a sundial might be located on a South-facing roof, for example. The hour-lines for such a sundial can be calculated by slightly correcting the horizontal formula above
:
where
is the desired angle of reclining relative to the local vertical, L is the sundial's geographical latitude,
is the angle between a given hour-line and the noon hour-line (which always points due north) on the plane, and ''t'' is the number of hours before or after noon. For example, the angle
of the 3pm hour-line would equal the
arctangent
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Spe ...
of
cos
Cos, COS, CoS, coS or Cos. may refer to:
Mathematics, science and technology
* Carbonyl sulfide
* Class of service (CoS or COS), a network header field defined by the IEEE 802.1p task group
* Class of service (COS), a parameter in telephone syst ...
(L + R), since tan 45° = 1. When R equals 0° (in other words, a South-facing vertical dial), we obtain the vertical dial formula above.
Some authors use a more specific nomenclature to describe the orientation of the shadow-receiving plane. If the plane's face points downwards towards the ground, it is said to be ''proclining'' or ''inclining'', whereas a dial is said to be ''reclining'' when the dial face is pointing away from the ground. Many authors also often refer to reclined, proclined and inclined sundials in general as inclined sundials. It is also common in the latter case to measure the angle of inclination relative to the horizontal plane on the sun side of the dial.
In such texts, since I = 90° + R, the hour angle formula will often be seen written as :
:
The angle between the gnomon style and the dial plate, B, in this type of sundial is :
:
Or :
:
Declining-reclining dials/ Declining-inclining dials
Some sundials both decline and recline, in that their shadow-receiving plane is not oriented with a cardinal direction (such as
true North or true South) and is neither horizontal nor vertical nor equatorial. For example, such a sundial might be found on a roof that was not oriented in a cardinal direction.
The formulae describing the spacing of the hour-lines on such dials are rather more complicated than those for simpler dials.
There are various solution approaches, including some using the methods of rotation matrices, and some making a 3D model of the reclined-declined plane and its vertical declined counterpart plane, extracting the geometrical relationships between the hour angle components on both these planes and then reducing the trigonometric algebra.
One system of formulas for Reclining-Declining sundials: (as stated by Fennewick)
The angle
between the noon hour-line and another hour-line is given by the formula below. Note that
advances counterclockwise with respect to the zero hour angle for those dials that are partly south-facing and clockwise for those that are north-facing.
:
within the parameter ranges :
and
.
Or, if preferring to use inclination angle,
, rather than the reclination,
, where
:
:
within the parameter ranges :
and
.
Here
is the sundial's geographical latitude;
is the orientation switch integer; ''t'' is the time in hours before or after noon; and
and
are the angles of reclination and declination, respectively.
Note that
is measured with reference to the vertical. It is positive when the dial leans back towards the horizon behind the dial and negative when the dial leans forward to the horizon on the Sun's side. Declination angle
is defined as positive when moving east of true south.
Dials facing fully or partly south have
= +1, while those partly or fully north-facing have an
value of -1.
Since the above expression gives the hour angle as an arctan function, due consideration must be given to which quadrant of the sundial each hour belongs to before assigning the correct hour angle.
Unlike the simpler vertical declining sundial, this type of dial does not always show hour angles on its sunside face for all declinations between east and west. When a northern hemisphere partly south-facing dial reclines back (i.e. away from the Sun) from the vertical, the gnomon will become co-planar with the dial plate at declinations less than due east or due west. Likewise for southern hemisphere dials that are partly north-facing.
Were these dials reclining forward, the range of declination would actually exceed due east and due west.
In a similar way, northern hemisphere dials that are partly north-facing and southern hemisphere dials that are south-facing, and which lean forward toward their upward pointing gnomons, will have a similar restriction on the range of declination that is possible for a given reclination value.
The critical declination
is a geometrical constraint which depends on the value of both the dial's reclination and its latitude :
:
As with the vertical declined dial, the gnomon's substyle is not aligned with the noon hour-line. The general formula for the angle
, between the substyle and the noon-line is given by :
:
The angle
, between the style and the plate is given by :
:
Note that for
, i.e. when the gnomon is coplanar with the dial plate, we have :
:
i.e. when
, the critical declination value.
[
]
Empirical method
Because of the complexity of the above calculations, using them for the practical purpose of designing a dial of this type is difficult and prone to error. It has been suggested that it is better to locate the hour lines empirically, marking the positions of the shadow of a style on a real sundial at hourly intervals as shown by a clock and adding/deducting that day's equation of time adjustment. See Empirical hour-line marking, above.
Spherical sundials
 The surface receiving the shadow need not be a plane, but can have any shape, provided that the sundial maker is willing to mark the hour-lines. If the style is aligned with the Earth's rotational axis, a spherical shape is convenient since the hour-lines are equally spaced, as they are on the equatorial dial shown here; the sundial is ''equiangular''. This is the principle behind the armillary sphere and the equatorial bow sundial. However, some equiangular sundials—such as the Lambert dial described below—are based on other principles.
In the ''equatorial bow sundial'', the gnomon is a bar, slot or stretched wire parallel to the celestial axis. The face is a semicircle, corresponding to the equator of the sphere, with markings on the inner surface. This pattern, built a couple of meters wide out of temperature-invariant steel invar, was used to keep the trains running on time in France before World War I.
Among the most precise sundials ever made are two equatorial bows constructed of
The surface receiving the shadow need not be a plane, but can have any shape, provided that the sundial maker is willing to mark the hour-lines. If the style is aligned with the Earth's rotational axis, a spherical shape is convenient since the hour-lines are equally spaced, as they are on the equatorial dial shown here; the sundial is ''equiangular''. This is the principle behind the armillary sphere and the equatorial bow sundial. However, some equiangular sundials—such as the Lambert dial described below—are based on other principles.
In the ''equatorial bow sundial'', the gnomon is a bar, slot or stretched wire parallel to the celestial axis. The face is a semicircle, corresponding to the equator of the sphere, with markings on the inner surface. This pattern, built a couple of meters wide out of temperature-invariant steel invar, was used to keep the trains running on time in France before World War I.
Among the most precise sundials ever made are two equatorial bows constructed of marble
Marble is a metamorphic rock composed of recrystallized carbonate minerals, most commonly calcite or dolomite. Marble is typically not foliated (layered), although there are exceptions. In geology, the term ''marble'' refers to metamorphose ...
found in Yantra mandir
A Jantar Mantar ( Hindustani pronunciation: ͡ʒən̪t̪ər mən̪t̪ər is an assembly of stone-built astronomical instruments, designed to be used with the naked eye. There were five Jantar Mantars in India, all of them built at the co ...
. This collection of sundials and other astronomical instruments was built by Maharaja Jai Singh II
Jai Singh II (3 November 1681 – 21 September 1743) popularly known as Sawai Jai Singh was the 29th Kachwaha Rajput ruler of the Kingdom of Amber, who later founded the fortified city of Jaipur and made it his capital. He was born at Amber, t ...
at his then-new capital of Jaipur
Jaipur (; Hindi: ''Jayapura''), formerly Jeypore, is the capital and largest city of the Indian state of Rajasthan. , the city had a population of 3.1 million, making it the tenth most populous city in the country. Jaipur is also known a ...
, India between 1727 and 1733. The larger equatorial bow is called the ''Samrat Yantra'' (The Supreme Instrument); standing at 27 meters, its shadow moves visibly at 1 mm per second, or roughly a hand's breadth (6 cm) every minute.
Cylindrical, conical, and other non-planar sundials
 Other non-planar surfaces may be used to receive the shadow of the gnomon.
As an elegant alternative, the style (which could be created by a hole or slit in the circumference) may be located on the circumference of a cylinder or sphere, rather than at its central axis of symmetry.
In that case, the hour lines are again spaced equally, but at ''twice'' the usual angle, due to the geometrical
Other non-planar surfaces may be used to receive the shadow of the gnomon.
As an elegant alternative, the style (which could be created by a hole or slit in the circumference) may be located on the circumference of a cylinder or sphere, rather than at its central axis of symmetry.
In that case, the hour lines are again spaced equally, but at ''twice'' the usual angle, due to the geometrical inscribed angle
In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Equivalently, an in ...
theorem. This is the basis of some modern sundials, but it was also used in ancient times;
In another variation of the polar-axis-aligned cylindrical, a cylindrical dial could be rendered as a helical ribbon-like surface, with a thin gnomon located either along its center or at its periphery.
Movable-gnomon sundials
Sundials can be designed with a gnomon that is placed in a different position each day throughout the year. In other words, the position of the gnomon relative to the centre of the hour lines varies. The gnomon need not be aligned with the celestial poles and may even be perfectly vertical (the analemmatic dial). These dials, when combined with fixed-gnomon sundials, allow the user to determine true North with no other aid; the two sundials are correctly aligned if and only if they both show the same time.
Universal equinoctial ring dial
 A ''universal equinoctial ring dial'' (sometimes called a ''ring dial'' for brevity, although the term is ambiguous), is a portable version of an armillary sundial, or was inspired by the mariner's astrolabe.
A ''universal equinoctial ring dial'' (sometimes called a ''ring dial'' for brevity, although the term is ambiguous), is a portable version of an armillary sundial, or was inspired by the mariner's astrolabe.[Swanick, Lois Ann. ''An Analysis Of Navigational Instruments In The Age Of Exploration: 15th Century To Mid-17th Century'', MA Thesis, Texas A&M University, December 2005] It was likely invented by William Oughtred around 1600 and became common throughout Europe.
In its simplest form, the style is a thin slit that allows the Sun's rays to fall on the hour-lines of an equatorial ring. As usual, the style is aligned with the Earth's axis; to do this, the user may orient the dial towards true North and suspend the ring dial vertically from the appropriate point on the meridian ring. Such dials may be made self-aligning with the addition of a more complicated central bar, instead of a simple slit-style. These bars are sometimes an addition to a set of Gemma's rings
Astronomical rings ( Latin: annuli astronomici), also known as Gemma's rings, are an early astronomical instrument. The instrument consists of three rings, representing the celestial equator, declination, and the meridian.
It can be used as a su ...
. This bar could pivot about its end points and held a perforated slider that was positioned to the month and day according to a scale scribed on the bar. The time was determined by rotating the bar towards the Sun so that the light shining through the hole fell on the equatorial ring. This forced the user to rotate the instrument, which had the effect of aligning the instrument's vertical ring with the meridian.
When not in use, the equatorial and meridian rings can be folded together into a small disk.
In 1610, Edward Wright created the sea ring, which mounted a universal ring dial over a magnetic compass. This permitted mariners to determine the time and magnetic variation in a single step.[May, William Edward, ''A History of Marine Navigation'', G. T. Foulis & Co. Ltd., Henley-on-Thames, Oxfordshire, 1973, ]
Analemmatic sundials
 Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. There are no hour lines on the dial and the time of day is read on the ellipse. The gnomon is not fixed and must change position daily to accurately indicate time of day.
Analemmatic sundials are sometimes designed with a human as the gnomon. Human gnomon analemmatic sundials are not practical at lower latitudes where a human shadow is quite short during the summer months. A 66 inch tall person casts a 4-inch shadow at 27 deg latitude on the summer solstice.
Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. There are no hour lines on the dial and the time of day is read on the ellipse. The gnomon is not fixed and must change position daily to accurately indicate time of day.
Analemmatic sundials are sometimes designed with a human as the gnomon. Human gnomon analemmatic sundials are not practical at lower latitudes where a human shadow is quite short during the summer months. A 66 inch tall person casts a 4-inch shadow at 27 deg latitude on the summer solstice.
Foster-Lambert dials
The Foster-Lambert dial is another movable-gnomon sundial. In contrast to the elliptical analemmatic dial, the Lambert dial is circular with evenly spaced hour lines, making it an ''equiangular sundial'', similar to the equatorial, spherical, cylindrical and conical dials described above. The gnomon of a Foster-Lambert dial is neither vertical nor aligned with the Earth's rotational axis; rather, it is tilted northwards by an angle α = 45° - (Φ/2), where Φ is the geographical latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
. Thus, a Foster-Lambert dial located at latitude 40° would have a gnomon tilted away from vertical by 25° in a northerly direction. To read the correct time, the gnomon must also be moved northwards by a distance
:
where ''R'' is the radius of the Foster-Lambert dial and δ again indicates the Sun's declination for that time of year.
Altitude-based sundials
 Altitude dials measure the height of the Sun in the sky, rather than directly measuring its hour-angle about the Earth's axis. They are not oriented towards true North, but rather towards the Sun and generally held vertically. The Sun's elevation is indicated by the position of a nodus, either the shadow-tip of a gnomon, or a spot of light.
In altitude dials, the time is read from where the nodus falls on a set of hour-curves that vary with the time of year. Many such altitude-dials' construction is calculation-intensive, as also the case with many azimuth dials. But the capuchin dials (described below) are constructed and used graphically.
Altitude dials' disadvantages:
Since the Sun's altitude is the same at times equally spaced about noon (e.g., 9am and 3pm), the user had to know whether it was morning or afternoon. At, say, 3:00 pm, that isn't a problem. But when the dial indicates a time 15 minutes from noon, the user likely won't have a way of distinguishing 11:45 from 12:15.
Additionally, altitude dials are less accurate near noon, because the sun's altitude isn't changing rapidly then.
Many of these dials are portable and simple to use. As is often the case with other sundials, many altitude dials are designed for only one latitude. But the capuchin dial (described below) has a version that's adjustable for latitude.
The book on sundials by Mayall & Mayall describes the Universal Capuchin sundial.
Altitude dials measure the height of the Sun in the sky, rather than directly measuring its hour-angle about the Earth's axis. They are not oriented towards true North, but rather towards the Sun and generally held vertically. The Sun's elevation is indicated by the position of a nodus, either the shadow-tip of a gnomon, or a spot of light.
In altitude dials, the time is read from where the nodus falls on a set of hour-curves that vary with the time of year. Many such altitude-dials' construction is calculation-intensive, as also the case with many azimuth dials. But the capuchin dials (described below) are constructed and used graphically.
Altitude dials' disadvantages:
Since the Sun's altitude is the same at times equally spaced about noon (e.g., 9am and 3pm), the user had to know whether it was morning or afternoon. At, say, 3:00 pm, that isn't a problem. But when the dial indicates a time 15 minutes from noon, the user likely won't have a way of distinguishing 11:45 from 12:15.
Additionally, altitude dials are less accurate near noon, because the sun's altitude isn't changing rapidly then.
Many of these dials are portable and simple to use. As is often the case with other sundials, many altitude dials are designed for only one latitude. But the capuchin dial (described below) has a version that's adjustable for latitude.
The book on sundials by Mayall & Mayall describes the Universal Capuchin sundial.
Human shadows
The length of a human shadow (or of any vertical object) can be used to measure the sun's elevation and, thence, the time. The Venerable Bede
Bede ( ; ang, Bǣda , ; 672/326 May 735), also known as Saint Bede, The Venerable Bede, and Bede the Venerable ( la, Beda Venerabilis), was an English monk at the monastery of St Peter and its companion monastery of St Paul in the Kingdom ...
gave a table for estimating the time from the length of one's shadow in feet, on the assumption that a monk's height is six times the length of his foot. Such shadow lengths will vary with the geographical latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
and with the time of year. For example, the shadow length at noon is short in summer months, and long in winter months.
Chaucer
Geoffrey Chaucer (; – 25 October 1400) was an English poet, author, and civil servant best known for '' The Canterbury Tales''. He has been called the "father of English literature", or, alternatively, the "father of English poetry". He w ...
evokes this method a few times in his ''Canterbury Tales
''The Canterbury Tales'' ( enm, Tales of Caunterbury) is a collection of twenty-four stories that runs to over 17,000 lines written in Middle English by Geoffrey Chaucer between 1387 and 1400. It is widely regarded as Chaucer's '' magnum opu ...
'', as in his ''Parson's Tale''.
An equivalent type of sundial using a vertical rod of fixed length is known as a '' backstaff dial''.
Shepherd's dial – timesticks
 A
A shepherd's dial
A shepherd's dial (also known as a pillar dial or cylinder) is a type of sundial that measures the height of the sun via the so-called '' umbra versa''. Its design needs to incorporate a fixed latitude, but it is small and portable. It is named ...
– also known as a ''shepherd's column dial'',Shakespeare
William Shakespeare ( 26 April 1564 – 23 April 1616) was an English playwright, poet and actor. He is widely regarded as the greatest writer in the English language and the world's pre-eminent dramatist. He is often called England's nation ...
's '' Henry VI, Part 3'' (Act 2, Scene 5, Lines 21-29), among other works of literature.
The cylindrical shepherd's dial can be unrolled into a flat plate. In one simple version, the front and back of the plate each have three columns, corresponding to pairs of months with roughly the same solar declination (June–July, May–August, April–September, March–October, February–November, and January–December). The top of each column has a hole for inserting the shadow-casting gnomon, a peg. Often only two times are marked on the column below, one for noon and the other for mid-morning/mid-afternoon.
Timesticks, ''clock spear'',
Ring dials
In a ring dial (also known as an ''Aquitaine'' or a ''perforated ring dial''), the ring is hung vertically and oriented sideways towards the sun. A beam of light passes through a small hole in the ring and falls on hour-curves that are inscribed on the inside of the ring. To adjust for the equation of time, the hole is usually on a loose ring within the ring so that the hole can be adjusted to reflect the current month.
Card dials (Capuchin dials)
Card dials are another form of altitude dial. A card is aligned edge-on with the sun and tilted so that a ray of light passes through an aperture onto a specified spot, thus determining the sun's altitude. A weighted string hangs vertically downwards from a hole in the card, and carries a bead or knot. The position of the bead on the hour-lines of the card gives the time. In more sophisticated versions such as the Capuchin dial, there is only one set of hour-lines, i.e., the hour lines do not vary with the seasons. Instead, the position of the hole from which the weighted string hangs is varied according to the season.
The Capuchin sundials are constructed and used graphically, as opposed the direct hour-angle measurements of horizontal or equatorial dials; or the calculated hour angle lines of some altitude and azimuth dials.
In addition to the ordinary Capuchin dial, there is a universal Capuchin dial, adjustable for latitude.
Navicula
 A
A navicula de Venetiis
A navicula de Venetiis or "little ship of Venice" was an altitude dial used to tell time and which was shaped like a little ship. The cursor (with a plumb line
A plumb bob, plumb bob level, or plummet, is a weight, usually with a pointed ti ...
or "little ship of Venice" was an altitude dial used to tell time and which was shaped like a little ship. The cursor (with a plumb line attached) was slid up/down the mast to the correct latitude. The user then sighted the Sun through the pair of sighting holes at either end of the "ship's deck". The plumb line then marked what hour of the day it was.
Nodus-based sundials
 Another type of sundial follows the motion of a single point of light or shadow, which may be called the ''nodus''. For example, the sundial may follow the sharp tip of a gnomon's shadow, e.g., the shadow-tip of a vertical
Another type of sundial follows the motion of a single point of light or shadow, which may be called the ''nodus''. For example, the sundial may follow the sharp tip of a gnomon's shadow, e.g., the shadow-tip of a vertical obelisk
An obelisk (; from grc, ὀβελίσκος ; diminutive of ''obelos'', " spit, nail, pointed pillar") is a tall, four-sided, narrow tapering monument which ends in a pyramid-like shape or pyramidion at the top. Originally constructed by An ...
(e.g., the '' Solarium Augusti'') or the tip of the horizontal marker in a shepherd's dial. Alternatively, sunlight may be allowed to pass through a small hole or reflected from a small (e.g., coin-sized) circular mirror, forming a small spot of light whose position may be followed. In such cases, the rays of light trace out a cone over the course of a day; when the rays fall on a surface, the path followed is the intersection of the cone with that surface. Most commonly, the receiving surface is a geometrical plane, so that the path of the shadow-tip or light-spot (called ''declination line'') traces out a conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a ...
such as a hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
or an ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
. The collection of hyperbolae was called a ''pelekonon'' (axe) by the Greeks, because it resembles a double-bladed ax, narrow in the center (near the noonline) and flaring out at the ends (early morning and late evening hours).
 There is a simple verification of hyperbolic declination lines on a sundial: the distance from the origin to the equinox line should be equal to harmonic mean of distances from the origin to summer and winter solstice lines.
Nodus-based sundials may use a small hole or mirror to isolate a single ray of light; the former are sometimes called ''aperture dials''. The oldest example is perhaps the antiborean sundial (''antiboreum''), a spherical nodus-based sundial that faces true North; a ray of sunlight enters from the South through a small hole located at the sphere's pole and falls on the hour and date lines inscribed within the sphere, which resemble lines of longitude and latitude, respectively, on a globe.
There is a simple verification of hyperbolic declination lines on a sundial: the distance from the origin to the equinox line should be equal to harmonic mean of distances from the origin to summer and winter solstice lines.
Nodus-based sundials may use a small hole or mirror to isolate a single ray of light; the former are sometimes called ''aperture dials''. The oldest example is perhaps the antiborean sundial (''antiboreum''), a spherical nodus-based sundial that faces true North; a ray of sunlight enters from the South through a small hole located at the sphere's pole and falls on the hour and date lines inscribed within the sphere, which resemble lines of longitude and latitude, respectively, on a globe.
Reflection sundials
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, Theology, theologian, and author (described in his time as a "natural philosophy, natural philosopher"), widely ...
developed a convenient and inexpensive sundial, in which a small mirror is placed on the sill of a south-facing window. The mirror acts like a nodus, casting a single spot of light on the ceiling. Depending on the geographical latitude
In geography, latitude is a coordinate that specifies the north– south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from –90° at the south pole to 90° at the north ...
and time of year, the light-spot follows a conic section, such as the hyperbolae of the pelikonon. If the mirror is parallel to the Earth's equator, and the ceiling is horizontal, then the resulting angles are those of a conventional horizontal sundial. Using the ceiling as a sundial surface exploits unused space, and the dial may be large enough to be very accurate.
Multiple dials
Sundials are sometimes combined into multiple dials. If two or more dials that operate on different principles — such as an analemmatic dial and a horizontal or vertical dial — are combined, the resulting multiple dial becomes self-aligning, most of the time. Both dials need to output both time and declination. In other words, the direction of true North need not be determined; the dials are oriented correctly when they read the same time and declination. However, the most common forms combine dials are based on the same principle and the analemmatic does not normally output the declination of the sun, thus are not self-aligning.
Diptych (tablet) sundial
 The diptych consisted of two small flat faces, joined by a hinge. Diptychs usually folded into little flat boxes suitable for a pocket. The gnomon was a string between the two faces. When the string was tight, the two faces formed both a vertical and horizontal sundial. These were made of white ivory, inlaid with black lacquer markings. The gnomons were black braided silk, linen or hemp string. With a knot or bead on the string as a nodus, and the correct markings, a diptych (really any sundial large enough) can keep a calendar well-enough to plant crops. A common error describes the diptych dial as self-aligning. This is not correct for diptych dials consisting of a horizontal and vertical dial using a string gnomon between faces, no matter the orientation of the dial faces. Since the string gnomon is continuous, the shadows must meet at the hinge; hence, ''any'' orientation of the dial will show the same time on both dials.
The diptych consisted of two small flat faces, joined by a hinge. Diptychs usually folded into little flat boxes suitable for a pocket. The gnomon was a string between the two faces. When the string was tight, the two faces formed both a vertical and horizontal sundial. These were made of white ivory, inlaid with black lacquer markings. The gnomons were black braided silk, linen or hemp string. With a knot or bead on the string as a nodus, and the correct markings, a diptych (really any sundial large enough) can keep a calendar well-enough to plant crops. A common error describes the diptych dial as self-aligning. This is not correct for diptych dials consisting of a horizontal and vertical dial using a string gnomon between faces, no matter the orientation of the dial faces. Since the string gnomon is continuous, the shadows must meet at the hinge; hence, ''any'' orientation of the dial will show the same time on both dials.
Multiface dials
A common type of multiple dial has sundials on every face of a Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all e ...
(regular polyhedron), usually a cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the only ...
.
Extremely ornate sundials can be composed in this way, by applying a sundial to every surface of a solid object.
In some cases, the sundials are formed as hollows in a solid object, e.g., a cylindrical hollow aligned with the Earth's rotational axis (in which the edges play the role of styles) or a spherical hollow in the ancient tradition of the ''hemisphaerium'' or the ''antiboreum''. (See the History section above.) In some cases, these multiface dials are small enough to sit on a desk, whereas in others, they are large stone monuments.
A Polyhedral's dial faces can be designed to give the time for different time-zones simultaneously. Examples include the Scottish sundial
Scottish sundials of the renaissance period are not just more numerous than in any other country, they are also stylistically unique. This is particularly notable when the size and wealth of Scotland at the time are taken into account. They ar ...
of the 17th and 18th century, which was often an extremely complex shape of polyhedral, and even convex, faces.
Prismatic dials
Prismatic dials are a special case of polar dials, in which the sharp edges of a prism of a concave polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two ...
serve as the styles and the sides of the prism receive the shadow. Examples include a three-dimensional cross or star of David on gravestones.
Unusual sundials
Benoy dial
 The Benoy dial was invented by Walter Gordon Benoy of
The Benoy dial was invented by Walter Gordon Benoy of Collingham, Nottinghamshire
Collingham is a village and civil parish in Nottinghamshire, England. The population (including Brough) at the 2011 Census was 2,738.
Collingham is located on the banks of the River Trent on the A1133 main road, just off the A46. It is appro ...
, England. Whereas a gnomon casts a sheet of shadow, his invention creates an equivalent sheet of light by allowing the Sun's rays through a thin slit, reflecting them from a long, slim mirror (usually half-cylindrical), or focusing them through a cylindrical lens. Examples of Benoy dials can be found in the United Kingdom at:[List correct as of British Sundial Register 2000. ]
*Carnfunnock Country Park, Antrim Northern Ireland
Northern Ireland ( ga, Tuaisceart Éireann ; sco, label=Ulster Scots dialect, Ulster-Scots, Norlin Airlann) is a part of the United Kingdom, situated in the north-east of the island of Ireland, that is #Descriptions, variously described as ...
*Upton Hall, British Horological Institute, Newark-on-Trent
Newark-on-Trent or Newark () is a market town and civil parish in the Newark and Sherwood district in Nottinghamshire, England. It is on the River Trent, and was historically a major inland port. The A1 road bypasses the town on the line ...
, Nottinghamshire
*Within the collections of St Edmundsbury Heritage Service, Bury St Edmunds
Bury St Edmunds (), commonly referred to locally as Bury, is a historic market, cathedral town and civil parish in Suffolk, England.OS Explorer map 211: Bury St.Edmunds and Stowmarket Scale: 1:25 000. Publisher:Ordnance Survey – Southampton ...
* Longleat, Wiltshire
* Jodrell Bank Science Centre
* Birmingham Botanical Gardens
* Science Museum, London (inventory number 1975-318)
Bifilar sundial
 Invented by the German mathematician Hugo Michnik in 1922, the
Invented by the German mathematician Hugo Michnik in 1922, the bifilar sundial
A bifilar dial is a type of sundial invented by the German mathematician Hugo Michnik in 1922. It has two non-touching threads parallel to the dial. Usually the second thread is orthogonal-(perpendicular) to the first.
The intersection of the ...
has two non-intersecting threads parallel to the dial. Usually the second thread is orthogonal to the first.
Digital sundial
A digital sundial indicates the current time with numerals formed by the sunlight striking it. Sundials of this type are installed in the Deutsches Museum
The Deutsches Museum (''German Museum'', officially (English: ''German Museum of Masterpieces of Science and Technology'')) in Munich, Germany, is the world's largest museum of science and technology, with about 28,000 exhibited objects from ...
in Munich and in the Sundial Park in Genk (Belgium), and a small version is available commercially. There is a patent for this type of sundial.Digital sundial
/ref>
Globe dial
The globe dial is a sphere aligned with the Earth's rotational axis, and equipped with a spherical vane. Similar to sundials with a fixed axial style, a globe dial determines the time from the Sun's azimuthal angle in its apparent rotation about the earth. This angle can be determined by rotating the vane to give the smallest shadow.
Noon marks
 The simplest sundials do not give the hours, but rather note the exact moment of 12:00 noon. In centuries past, such dials were used to set mechanical clocks, which were sometimes so inaccurate as to lose or gain significant time in a single day. The simplest noon-marks have a shadow that passes a mark. Then, an almanac can translate from local solar time and date to civil time. The civil time is used to set the clock. Some noon-marks include a figure-eight that embodies the equation of time, so that no almanac is needed.
In some U.S. colonial-era houses, a noon-mark might be carved into a floor or windowsill. Such marks indicate local noon, and provide a simple and accurate time reference for households to set their clocks. Some Asian countries had post offices set their clocks from a precision noon-mark. These in turn provided the times for the rest of the society. The typical noon-mark sundial was a lens set above an
The simplest sundials do not give the hours, but rather note the exact moment of 12:00 noon. In centuries past, such dials were used to set mechanical clocks, which were sometimes so inaccurate as to lose or gain significant time in a single day. The simplest noon-marks have a shadow that passes a mark. Then, an almanac can translate from local solar time and date to civil time. The civil time is used to set the clock. Some noon-marks include a figure-eight that embodies the equation of time, so that no almanac is needed.
In some U.S. colonial-era houses, a noon-mark might be carved into a floor or windowsill. Such marks indicate local noon, and provide a simple and accurate time reference for households to set their clocks. Some Asian countries had post offices set their clocks from a precision noon-mark. These in turn provided the times for the rest of the society. The typical noon-mark sundial was a lens set above an analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same mean solar time, as that position varies over the course of a year. The diagram will resemble a figur ...
tic plate. The plate has an engraved figure-eight shape, which corresponds to the equation of time (described above) versus the solar declination. When the edge of the Sun's image touches the part of the shape for the current month, this indicates that it is 12:00 noon.
Sundial cannon
A sundial cannon
A sundial cannon, sundial gun, noon cannon or meridian cannon, also noonday gun is a device consisting of a sundial incorporating a cannon with a fuse that is lit by an overhanging lens, concentrating the rays of the sun, and causing the cannon to ...
, sometimes called a 'meridian cannon', is a specialized sundial that is designed to create an 'audible noonmark', by automatically igniting a quantity of gunpowder at noon. These were novelties rather than precision sundials, sometimes installed in parks in Europe mainly in the late 18th or early 19th century. They typically consist of a horizontal sundial, which has in addition to a gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields.
History
A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the ...
a suitably mounted lens, set to focus the rays of the sun at exactly noon on the firing pan of a miniature cannon
A cannon is a large- caliber gun classified as a type of artillery, which usually launches a projectile using explosive chemical propellant. Gunpowder ("black powder") was the primary propellant before the invention of smokeless powder ...
loaded with gunpowder
Gunpowder, also commonly known as black powder to distinguish it from modern smokeless powder, is the earliest known chemical explosive. It consists of a mixture of sulfur, carbon (in the form of charcoal) and potassium nitrate (saltpeter). T ...
(but no ball). To function properly the position and angle of the lens must be adjusted seasonally.
Meridian lines
A horizontal line aligned on a meridian with a gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields.
History
A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the ...
facing the noon-sun is termed a meridian line and does not indicate the time, but instead the day of the year. Historically they were used to accurately determine the length of the solar year. Examples are the Bianchini
Bianchini is an Italian surname. Notable people with the surname include:
* Angela Bianchini (1921–2018), Italian fiction writer and literary critic
* Brian Bianchini (1978–2004), American male model
* Francesco Bianchini (1662–1729), Ital ...
meridian line in Santa Maria degli Angeli e dei Martiri in Rome
, established_title = Founded
, established_date = 753 BC
, founder = King Romulus ( legendary)
, image_map = Map of comune of Rome (metropolitan city of Capital Rome, region Lazio, Italy).svg
, map_caption ...
, and the Cassini line in San Petronio Basilica
The Basilica of San Petronio is a minor basilica and church of the Archdiocese of Bologna located in Bologna, Emilia Romagna, northern Italy. It dominates Piazza Maggiore. The basilica is dedicated to the patron saint of the city, Saint Petroniu ...
at Bologna
Bologna (, , ; egl, label= Emilian, Bulåggna ; lat, Bononia) is the capital and largest city of the Emilia-Romagna region in Northern Italy. It is the seventh most populous city in Italy with about 400,000 inhabitants and 150 different na ...
.
Sundial mottoes
The association of sundials with time has inspired their designers over the centuries to display mottoes as part of the design. Often these cast the device in the role of '' memento mori'', inviting the observer to reflect on the transience of the world and the inevitability of death. "Do not kill time, for it will surely kill thee." Other mottoes are more whimsical: "I count only the sunny hours," and "I am a sundial and I make a botch / of what is done far better by a watch." Collections of sundial mottoes have often been published through the centuries.
Use as a compass
If a horizontal-plate sundial is made for the latitude in which it is being used, and if it is mounted with its plate horizontal and its gnomon pointing to the celestial pole that is above the horizon, then it shows the correct time in apparent solar time. Conversely, if the directions of the cardinal point
The four cardinal directions, or cardinal points, are the four main compass directions: north, east, south, and west, commonly denoted by their initials N, E, S, and W respectively. Relative to north, the directions east, south, and west are a ...
s are initially unknown, but the sundial is aligned so it shows the correct apparent solar time as calculated from the reading of a clock
A clock or a timepiece is a device used to measure and indicate time. The clock is one of the oldest human inventions, meeting the need to measure intervals of time shorter than the natural units such as the day, the lunar month and ...
, its gnomon shows the direction of True North or South, allowing the sundial to be used as a compass. The sundial can be placed on a horizontal surface, and rotated about a vertical axis until it shows the correct time. The gnomon will then be pointing to the North, in the northern hemisphere
The Northern Hemisphere is the half of Earth that is north of the Equator. For other planets in the Solar System, north is defined as being in the same celestial hemisphere relative to the invariable plane of the solar system as Earth's Nort ...
, or to the South in the southern hemisphere. This method is much more accurate than using a watch as a compass (see Cardinal direction#Watch face) and can be used in places where the magnetic declination is large, making a magnetic compass unreliable. An alternative method uses two sundials of different designs. (See #Multiple dials, above.) The dials are attached to and aligned with each other, and are oriented so they show the same time. This allows the directions of the cardinal points and the apparent solar time to be determined simultaneously, without requiring a clock.
See also
 *
* Butterfield dial
A Butterfield dial is a portable horizontal sundial designed to be folded flat and used in latitudes between 35° and 60°. It was named after the English gnomonist Michael Butterfield, who was active in Paris around 1690.
Description
The dials ...
* Equation clock
An equation clock is a mechanical clock which includes a mechanism that simulates the equation of time, so that the user can read or calculate solar time, as would be shown by a sundial. The first accurate clocks, controlled by pendulums, were ...
* Foucault pendulum
The Foucault pendulum or Foucault's pendulum is a simple device named after French physicist Léon Foucault, conceived as an experiment to demonstrate the Earth's rotation. A long and heavy pendulum suspended from the high roof above a circular ...
* Francesco Bianchini
* Horology
* Jantar Mantar
A Jantar Mantar ( Hindustani pronunciation: ͡ʒən̪t̪ər mən̪t̪ər is an assembly of stone-built astronomical instruments, designed to be used with the naked eye. There were five Jantar Mantars in India, all of them built at the com ...
* Lahaina Noon
* Moondial
Moondials are time pieces similar to a sundial
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the apparent position of the Sun in the sky. In the ...
* Nocturnal—device for determining time by the stars at night.
* Qibla observation by shadows
* Schema for horizontal dials A schema for horizontal dials is a set of instructions used to construct horizontal sundials using compass and straightedge construction techniques, which were widely used in Europe from the late fifteenth century to the late nineteenth century. The ...
—pen and ruler constructions
* Schema for vertical declining dials
Vertical declining dials are sundials that indicate local apparent time. Vertical south dials are a special case: as are vertical north, vertical east and vertical west dials. The word declining means that the wall is offset from one of these 4 c ...
—pen and ruler constructions
* Sciothericum telescopicum Sciothericum telescopicum was a sundial (sciothericum) that incorporated a telescope (telescopicum) for greater accuracy in determining exactly when noon occurred. It was invented by William Molyneux in Ireland in 1686. The device used a telescop ...
—a sundial invented in the 17th century that used a telescopic sight to determine the time of noon to within 15 seconds.
* Scottish sundial
Scottish sundials of the renaissance period are not just more numerous than in any other country, they are also stylistically unique. This is particularly notable when the size and wealth of Scotland at the time are taken into account. They ar ...
—the ancient renaissance sundials of Scotland.
* Shadows—free software for calculating and drawing sundials.
* Societat Catalana de Gnomònica
* Tide (time)—divisions of the day on early sundials.
* Wilanów Palace Sundial, created by Johannes Hevelius in about 1684.
* Zero shadow day
Notes
References
Citations
Sources
*
*
* Reprint of the 1902 book published by Macmillan (New York).
* Heilbron, J. L. : ''The sun in the church: cathedrals as solar observatories'', Harvard University Press
Harvard University Press (HUP) is a publishing house established on January 13, 1913, as a division of Harvard University, and focused on academic publishing. It is a member of the Association of American University Presses. After the retir ...
, 2001 .
* A.P. Herbert, ''Sundials Old and New'', Methuen & Co. Ltd, 1967.
* Kern, Ralf : Wissenschaftliche Instrumente in ihrer Zeit. Vom 15. – 19. Jahrhundert. Verlag der Buchhandlung Walther König 2010,
*
* Hugo Michnik, ''Theorie einer Bifilar-Sonnenuhr'', Astronomishe Nachrichten, 217(5190), pp. 81–90, 1923
* Slightly amended reprint of the 1970 translation published by University of Toronto Press (Toronto). The original was published in 1965 under the title ''Les Cadrans solaires'' by Gauthier-Villars (Montrouge, France).
* Savoie, Denis: ''Sundials, Design, Construction, and Use'', Springer, 2009, .
* Frederick W. Sawyer, ''Bifilar gnomonics'', JBAA (Journal of the British Astronomical association), 88(4):334–351, 1978
*
*
* Walker, Brown: ''Make A Sundial'', (The Education Group British Sundial Society) Editors Jane Walker and David Brown, British Sundial Society 1991
*
External links
National organisations
Asociación Amigos de los Relojes de Sol
(AARS) – Spanish Sundial Society
British Sundial Society
(BSS) – British Sundial Society
Commission des Cadrans Solaires de la Société Astronomique de France
French Sundial Society
Coordinamento Gnomonico Italiano
(CGI) – Italian Sundial Society
North American Sundial Society
(NASS) – North American Sundial Society
Societat Catalana de Gnomònica
– Catalan Sundial Society
De Zonnewijzerkring
– Dutch Sundial Society (in English)
Zonnewijzerkring Vlaanderen
– Flemish Sundial Society
Historical
"The Book of Remedies from Deficiencies in Setting Up Marble Sundials"
is an Arabic manuscript from 1319 about timekeeping and sundials.
"Small Treatise on the Calculation of Tables for the Construction of Inclined Sundials"
is another Arabic manuscript, from the 16th century, about the mathematical calculations used to create sundials. It was written by Sibt al-Maridini
Sibt al-Maridini, full name Muḥammad ibn Muḥammad ibn Aḥmad Abū ʿAbd Allāh Badr hamsal‐Dīnal‐Miṣrī al‐Dimashqī (1423 – 1506 AD), was an astronomer and mathematician. () His father came from Damascus. The word "Sibt al-Ma ...
.
Vodolazhskaya, L. Analemmatic and Horizontal Sundials of the Bronze Age (Northern Black Sea Coast). ''Archaeoastronomy and Ancient Technologies'' 1(1), 2013, 68-88
Reconstruction of ancient Egyptian sundials
Other
The British Sundial Society including a register of British sundials
Register of Scottish Sundials
The Ancient Vedic Sun Dial
World Sundial Atlas
Real Sun Time
– Sundial as a mobile or desktop version.
{{Authority control
Ancient inventions
Architectural elements
Clocks
Egyptian inventions
Garden ornaments
Horology
Outdoor sculptures


 A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct
A sundial is a horological device that tells the time of day (referred to as civil time in modern usage) when direct  The principles of sundials are understood most easily from the Sun's apparent motion. The Earth rotates on its axis, and revolves in an elliptical orbit around the Sun. An excellent approximation assumes that the Sun revolves around a stationary Earth on the celestial sphere, which rotates every 24 hours about its celestial axis. The celestial axis is the line connecting the celestial poles. Since the celestial axis is aligned with the axis about which the Earth rotates, the angle of the axis with the local horizontal is the local geographical
The principles of sundials are understood most easily from the Sun's apparent motion. The Earth rotates on its axis, and revolves in an elliptical orbit around the Sun. An excellent approximation assumes that the Sun revolves around a stationary Earth on the celestial sphere, which rotates every 24 hours about its celestial axis. The celestial axis is the line connecting the celestial poles. Since the celestial axis is aligned with the axis about which the Earth rotates, the angle of the axis with the local horizontal is the local geographical  This model of the Sun's motion helps to understand sundials. If the shadow-casting gnomon is aligned with the celestial poles, its shadow will revolve at a constant rate, and this rotation will not change with the seasons. This is the most common design. In such cases, the same hour lines may be used throughout the year. The hour-lines will be spaced uniformly if the surface receiving the shadow is either perpendicular (as in the equatorial sundial) or circular about the gnomon (as in the armillary sphere).
In other cases, the hour-lines are not spaced evenly, even though the shadow rotates uniformly. If the gnomon is ''not'' aligned with the celestial poles, even its shadow will not rotate uniformly, and the hour lines must be corrected accordingly. The rays of light that graze the tip of a gnomon, or which pass through a small hole, or reflect from a small mirror, trace out a cone aligned with the celestial poles. The corresponding light-spot or shadow-tip, if it falls onto a flat surface, will trace out a
This model of the Sun's motion helps to understand sundials. If the shadow-casting gnomon is aligned with the celestial poles, its shadow will revolve at a constant rate, and this rotation will not change with the seasons. This is the most common design. In such cases, the same hour lines may be used throughout the year. The hour-lines will be spaced uniformly if the surface receiving the shadow is either perpendicular (as in the equatorial sundial) or circular about the gnomon (as in the armillary sphere).
In other cases, the hour-lines are not spaced evenly, even though the shadow rotates uniformly. If the gnomon is ''not'' aligned with the celestial poles, even its shadow will not rotate uniformly, and the hour lines must be corrected accordingly. The rays of light that graze the tip of a gnomon, or which pass through a small hole, or reflect from a small mirror, trace out a cone aligned with the celestial poles. The corresponding light-spot or shadow-tip, if it falls onto a flat surface, will trace out a 
 The earliest sundials known from the archaeological record are shadow clocks (1500 BC or BCE) from ancient
The earliest sundials known from the archaeological record are shadow clocks (1500 BC or BCE) from ancient  A sundial at a particular
A sundial at a particular  The
The  An analemma may be added to many types of sundials to correct apparent solar time to
An analemma may be added to many types of sundials to correct apparent solar time to 
 The distinguishing characteristic of the ''equatorial dial'' (also called the ''equinoctial dial'') is the planar surface that receives the shadow, which is exactly perpendicular to the gnomon's style. This plane is called equatorial, because it is parallel to the equator of the Earth and of the celestial sphere. If the gnomon is fixed and aligned with the Earth's rotational axis, the sun's apparent rotation about the Earth casts a uniformly rotating sheet of shadow from the gnomon; this produces a uniformly rotating line of shadow on the equatorial plane. Since the Earth rotates 360° in 24 hours, the hour-lines on an equatorial dial are all spaced 15° apart (360/24).
:
The uniformity of their spacing makes this type of sundial easy to construct. If the dial plate material is opaque, both sides of the equatorial dial must be marked, since the shadow will be cast from below in winter and from above in summer. With translucent dial plates (e.g. glass) the hour angles need only be marked on the sun-facing side, although the hour numberings (if used) need be made on both sides of the dial, owing to the differing hour schema on the sun-facing and sun-backing sides.
Another major advantage of this dial is that equation of time (EoT) and daylight saving time (DST) corrections can be made by simply rotating the dial plate by the appropriate angle each day. This is because the hour angles are equally spaced around the dial. For this reason, an equatorial dial is often a useful choice when the dial is for public display and it is desirable to have it show the true local time to reasonable accuracy. The EoT correction is made via the relation
:
Near the equinoxes in spring and autumn, the sun moves on a circle that is nearly the same as the equatorial plane; hence, no clear shadow is produced on the equatorial dial at those times of year, a drawback of the design.
A ''nodus'' is sometimes added to equatorial sundials, which allows the sundial to tell the time of year. On any given day, the shadow of the nodus moves on a circle on the equatorial plane, and the radius of the circle measures the declination of the sun. The ends of the gnomon bar may be used as the nodus, or some feature along its length. An ancient variant of the equatorial sundial has only a nodus (no style) and the concentric circular hour-lines are arranged to resemble a spider-web.
The distinguishing characteristic of the ''equatorial dial'' (also called the ''equinoctial dial'') is the planar surface that receives the shadow, which is exactly perpendicular to the gnomon's style. This plane is called equatorial, because it is parallel to the equator of the Earth and of the celestial sphere. If the gnomon is fixed and aligned with the Earth's rotational axis, the sun's apparent rotation about the Earth casts a uniformly rotating sheet of shadow from the gnomon; this produces a uniformly rotating line of shadow on the equatorial plane. Since the Earth rotates 360° in 24 hours, the hour-lines on an equatorial dial are all spaced 15° apart (360/24).
:
The uniformity of their spacing makes this type of sundial easy to construct. If the dial plate material is opaque, both sides of the equatorial dial must be marked, since the shadow will be cast from below in winter and from above in summer. With translucent dial plates (e.g. glass) the hour angles need only be marked on the sun-facing side, although the hour numberings (if used) need be made on both sides of the dial, owing to the differing hour schema on the sun-facing and sun-backing sides.
Another major advantage of this dial is that equation of time (EoT) and daylight saving time (DST) corrections can be made by simply rotating the dial plate by the appropriate angle each day. This is because the hour angles are equally spaced around the dial. For this reason, an equatorial dial is often a useful choice when the dial is for public display and it is desirable to have it show the true local time to reasonable accuracy. The EoT correction is made via the relation
:
Near the equinoxes in spring and autumn, the sun moves on a circle that is nearly the same as the equatorial plane; hence, no clear shadow is produced on the equatorial dial at those times of year, a drawback of the design.
A ''nodus'' is sometimes added to equatorial sundials, which allows the sundial to tell the time of year. On any given day, the shadow of the nodus moves on a circle on the equatorial plane, and the radius of the circle measures the declination of the sun. The ends of the gnomon bar may be used as the nodus, or some feature along its length. An ancient variant of the equatorial sundial has only a nodus (no style) and the concentric circular hour-lines are arranged to resemble a spider-web.

 In the common ''vertical dial'', the shadow-receiving plane is aligned vertically; as usual, the gnomon's style is aligned with the Earth's axis of rotation. As in the horizontal dial, the line of shadow does not move uniformly on the face; the sundial is not ''equiangular''. If the face of the vertical dial points directly south, the angle of the hour-lines is instead described by the formula
:
where L is the sundial's geographical
In the common ''vertical dial'', the shadow-receiving plane is aligned vertically; as usual, the gnomon's style is aligned with the Earth's axis of rotation. As in the horizontal dial, the line of shadow does not move uniformly on the face; the sundial is not ''equiangular''. If the face of the vertical dial points directly south, the angle of the hour-lines is instead described by the formula
:
where L is the sundial's geographical  Vertical dials are commonly mounted on the walls of buildings, such as town-halls,
Vertical dials are commonly mounted on the walls of buildings, such as town-halls,  In ''polar dials'', the shadow-receiving plane is aligned ''parallel'' to the gnomon-style.
Thus, the shadow slides sideways over the surface, moving perpendicularly to itself as the Sun rotates about the style. As with the gnomon, the hour-lines are all aligned with the Earth's rotational axis. When the Sun's rays are nearly parallel to the plane, the shadow moves very quickly and the hour lines are spaced far apart. The direct East- and West-facing dials are examples of a polar dial. However, the face of a polar dial need not be vertical; it need only be parallel to the gnomon. Thus, a plane inclined at the angle of latitude (relative to horizontal) under the similarly inclined gnomon will be a polar dial. The perpendicular spacing ''X'' of the hour-lines in the plane is described by the formula
:
where ''H'' is the height of the style above the plane, and ''t'' is the time (in hours) before or after the center-time for the polar dial. The center time is the time when the style's shadow falls directly down on the plane; for an East-facing dial, the center time will be 6am, for a West-facing dial, this will be 6pm, and for the inclined dial described above, it will be noon. When ''t'' approaches ±6 hours away from the center time, the spacing ''X'' diverges to +∞; this occurs when the Sun's rays become parallel to the plane.
In ''polar dials'', the shadow-receiving plane is aligned ''parallel'' to the gnomon-style.
Thus, the shadow slides sideways over the surface, moving perpendicularly to itself as the Sun rotates about the style. As with the gnomon, the hour-lines are all aligned with the Earth's rotational axis. When the Sun's rays are nearly parallel to the plane, the shadow moves very quickly and the hour lines are spaced far apart. The direct East- and West-facing dials are examples of a polar dial. However, the face of a polar dial need not be vertical; it need only be parallel to the gnomon. Thus, a plane inclined at the angle of latitude (relative to horizontal) under the similarly inclined gnomon will be a polar dial. The perpendicular spacing ''X'' of the hour-lines in the plane is described by the formula
:
where ''H'' is the height of the style above the plane, and ''t'' is the time (in hours) before or after the center-time for the polar dial. The center time is the time when the style's shadow falls directly down on the plane; for an East-facing dial, the center time will be 6am, for a West-facing dial, this will be 6pm, and for the inclined dial described above, it will be noon. When ''t'' approaches ±6 hours away from the center time, the spacing ''X'' diverges to +∞; this occurs when the Sun's rays become parallel to the plane.
 A ''declining dial'' is any non-horizontal, planar dial that does not face in a cardinal direction, such as (true)
A ''declining dial'' is any non-horizontal, planar dial that does not face in a cardinal direction, such as (true)  The sundials described above have gnomons that are aligned with the Earth's rotational axis and cast their shadow onto a plane. If the plane is neither vertical nor horizontal nor equatorial, the sundial is said to be ''reclining'' or ''inclining''. Such a sundial might be located on a South-facing roof, for example. The hour-lines for such a sundial can be calculated by slightly correcting the horizontal formula above
:
where is the desired angle of reclining relative to the local vertical, L is the sundial's geographical latitude, is the angle between a given hour-line and the noon hour-line (which always points due north) on the plane, and ''t'' is the number of hours before or after noon. For example, the angle of the 3pm hour-line would equal the
The sundials described above have gnomons that are aligned with the Earth's rotational axis and cast their shadow onto a plane. If the plane is neither vertical nor horizontal nor equatorial, the sundial is said to be ''reclining'' or ''inclining''. Such a sundial might be located on a South-facing roof, for example. The hour-lines for such a sundial can be calculated by slightly correcting the horizontal formula above
:
where is the desired angle of reclining relative to the local vertical, L is the sundial's geographical latitude, is the angle between a given hour-line and the noon hour-line (which always points due north) on the plane, and ''t'' is the number of hours before or after noon. For example, the angle of the 3pm hour-line would equal the  The surface receiving the shadow need not be a plane, but can have any shape, provided that the sundial maker is willing to mark the hour-lines. If the style is aligned with the Earth's rotational axis, a spherical shape is convenient since the hour-lines are equally spaced, as they are on the equatorial dial shown here; the sundial is ''equiangular''. This is the principle behind the armillary sphere and the equatorial bow sundial. However, some equiangular sundials—such as the Lambert dial described below—are based on other principles.
In the ''equatorial bow sundial'', the gnomon is a bar, slot or stretched wire parallel to the celestial axis. The face is a semicircle, corresponding to the equator of the sphere, with markings on the inner surface. This pattern, built a couple of meters wide out of temperature-invariant steel invar, was used to keep the trains running on time in France before World War I.
Among the most precise sundials ever made are two equatorial bows constructed of
The surface receiving the shadow need not be a plane, but can have any shape, provided that the sundial maker is willing to mark the hour-lines. If the style is aligned with the Earth's rotational axis, a spherical shape is convenient since the hour-lines are equally spaced, as they are on the equatorial dial shown here; the sundial is ''equiangular''. This is the principle behind the armillary sphere and the equatorial bow sundial. However, some equiangular sundials—such as the Lambert dial described below—are based on other principles.
In the ''equatorial bow sundial'', the gnomon is a bar, slot or stretched wire parallel to the celestial axis. The face is a semicircle, corresponding to the equator of the sphere, with markings on the inner surface. This pattern, built a couple of meters wide out of temperature-invariant steel invar, was used to keep the trains running on time in France before World War I.
Among the most precise sundials ever made are two equatorial bows constructed of  Other non-planar surfaces may be used to receive the shadow of the gnomon.
As an elegant alternative, the style (which could be created by a hole or slit in the circumference) may be located on the circumference of a cylinder or sphere, rather than at its central axis of symmetry.
In that case, the hour lines are again spaced equally, but at ''twice'' the usual angle, due to the geometrical
Other non-planar surfaces may be used to receive the shadow of the gnomon.
As an elegant alternative, the style (which could be created by a hole or slit in the circumference) may be located on the circumference of a cylinder or sphere, rather than at its central axis of symmetry.
In that case, the hour lines are again spaced equally, but at ''twice'' the usual angle, due to the geometrical  A ''universal equinoctial ring dial'' (sometimes called a ''ring dial'' for brevity, although the term is ambiguous), is a portable version of an armillary sundial, or was inspired by the mariner's astrolabe.Swanick, Lois Ann. ''An Analysis Of Navigational Instruments In The Age Of Exploration: 15th Century To Mid-17th Century'', MA Thesis, Texas A&M University, December 2005 It was likely invented by William Oughtred around 1600 and became common throughout Europe.
In its simplest form, the style is a thin slit that allows the Sun's rays to fall on the hour-lines of an equatorial ring. As usual, the style is aligned with the Earth's axis; to do this, the user may orient the dial towards true North and suspend the ring dial vertically from the appropriate point on the meridian ring. Such dials may be made self-aligning with the addition of a more complicated central bar, instead of a simple slit-style. These bars are sometimes an addition to a set of
A ''universal equinoctial ring dial'' (sometimes called a ''ring dial'' for brevity, although the term is ambiguous), is a portable version of an armillary sundial, or was inspired by the mariner's astrolabe.Swanick, Lois Ann. ''An Analysis Of Navigational Instruments In The Age Of Exploration: 15th Century To Mid-17th Century'', MA Thesis, Texas A&M University, December 2005 It was likely invented by William Oughtred around 1600 and became common throughout Europe.
In its simplest form, the style is a thin slit that allows the Sun's rays to fall on the hour-lines of an equatorial ring. As usual, the style is aligned with the Earth's axis; to do this, the user may orient the dial towards true North and suspend the ring dial vertically from the appropriate point on the meridian ring. Such dials may be made self-aligning with the addition of a more complicated central bar, instead of a simple slit-style. These bars are sometimes an addition to a set of  Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. There are no hour lines on the dial and the time of day is read on the ellipse. The gnomon is not fixed and must change position daily to accurately indicate time of day.
Analemmatic sundials are sometimes designed with a human as the gnomon. Human gnomon analemmatic sundials are not practical at lower latitudes where a human shadow is quite short during the summer months. A 66 inch tall person casts a 4-inch shadow at 27 deg latitude on the summer solstice.
Analemmatic sundials are a type of horizontal sundial that has a vertical gnomon and hour markers positioned in an elliptical pattern. There are no hour lines on the dial and the time of day is read on the ellipse. The gnomon is not fixed and must change position daily to accurately indicate time of day.
Analemmatic sundials are sometimes designed with a human as the gnomon. Human gnomon analemmatic sundials are not practical at lower latitudes where a human shadow is quite short during the summer months. A 66 inch tall person casts a 4-inch shadow at 27 deg latitude on the summer solstice.
 Altitude dials measure the height of the Sun in the sky, rather than directly measuring its hour-angle about the Earth's axis. They are not oriented towards true North, but rather towards the Sun and generally held vertically. The Sun's elevation is indicated by the position of a nodus, either the shadow-tip of a gnomon, or a spot of light.
In altitude dials, the time is read from where the nodus falls on a set of hour-curves that vary with the time of year. Many such altitude-dials' construction is calculation-intensive, as also the case with many azimuth dials. But the capuchin dials (described below) are constructed and used graphically.
Altitude dials' disadvantages:
Since the Sun's altitude is the same at times equally spaced about noon (e.g., 9am and 3pm), the user had to know whether it was morning or afternoon. At, say, 3:00 pm, that isn't a problem. But when the dial indicates a time 15 minutes from noon, the user likely won't have a way of distinguishing 11:45 from 12:15.
Additionally, altitude dials are less accurate near noon, because the sun's altitude isn't changing rapidly then.
Many of these dials are portable and simple to use. As is often the case with other sundials, many altitude dials are designed for only one latitude. But the capuchin dial (described below) has a version that's adjustable for latitude.
The book on sundials by Mayall & Mayall describes the Universal Capuchin sundial.
Altitude dials measure the height of the Sun in the sky, rather than directly measuring its hour-angle about the Earth's axis. They are not oriented towards true North, but rather towards the Sun and generally held vertically. The Sun's elevation is indicated by the position of a nodus, either the shadow-tip of a gnomon, or a spot of light.
In altitude dials, the time is read from where the nodus falls on a set of hour-curves that vary with the time of year. Many such altitude-dials' construction is calculation-intensive, as also the case with many azimuth dials. But the capuchin dials (described below) are constructed and used graphically.
Altitude dials' disadvantages:
Since the Sun's altitude is the same at times equally spaced about noon (e.g., 9am and 3pm), the user had to know whether it was morning or afternoon. At, say, 3:00 pm, that isn't a problem. But when the dial indicates a time 15 minutes from noon, the user likely won't have a way of distinguishing 11:45 from 12:15.
Additionally, altitude dials are less accurate near noon, because the sun's altitude isn't changing rapidly then.
Many of these dials are portable and simple to use. As is often the case with other sundials, many altitude dials are designed for only one latitude. But the capuchin dial (described below) has a version that's adjustable for latitude.
The book on sundials by Mayall & Mayall describes the Universal Capuchin sundial.
 A
A  A
A  There is a simple verification of hyperbolic declination lines on a sundial: the distance from the origin to the equinox line should be equal to harmonic mean of distances from the origin to summer and winter solstice lines.
Nodus-based sundials may use a small hole or mirror to isolate a single ray of light; the former are sometimes called ''aperture dials''. The oldest example is perhaps the antiborean sundial (''antiboreum''), a spherical nodus-based sundial that faces true North; a ray of sunlight enters from the South through a small hole located at the sphere's pole and falls on the hour and date lines inscribed within the sphere, which resemble lines of longitude and latitude, respectively, on a globe.
There is a simple verification of hyperbolic declination lines on a sundial: the distance from the origin to the equinox line should be equal to harmonic mean of distances from the origin to summer and winter solstice lines.
Nodus-based sundials may use a small hole or mirror to isolate a single ray of light; the former are sometimes called ''aperture dials''. The oldest example is perhaps the antiborean sundial (''antiboreum''), a spherical nodus-based sundial that faces true North; a ray of sunlight enters from the South through a small hole located at the sphere's pole and falls on the hour and date lines inscribed within the sphere, which resemble lines of longitude and latitude, respectively, on a globe.
 The diptych consisted of two small flat faces, joined by a hinge. Diptychs usually folded into little flat boxes suitable for a pocket. The gnomon was a string between the two faces. When the string was tight, the two faces formed both a vertical and horizontal sundial. These were made of white ivory, inlaid with black lacquer markings. The gnomons were black braided silk, linen or hemp string. With a knot or bead on the string as a nodus, and the correct markings, a diptych (really any sundial large enough) can keep a calendar well-enough to plant crops. A common error describes the diptych dial as self-aligning. This is not correct for diptych dials consisting of a horizontal and vertical dial using a string gnomon between faces, no matter the orientation of the dial faces. Since the string gnomon is continuous, the shadows must meet at the hinge; hence, ''any'' orientation of the dial will show the same time on both dials.
The diptych consisted of two small flat faces, joined by a hinge. Diptychs usually folded into little flat boxes suitable for a pocket. The gnomon was a string between the two faces. When the string was tight, the two faces formed both a vertical and horizontal sundial. These were made of white ivory, inlaid with black lacquer markings. The gnomons were black braided silk, linen or hemp string. With a knot or bead on the string as a nodus, and the correct markings, a diptych (really any sundial large enough) can keep a calendar well-enough to plant crops. A common error describes the diptych dial as self-aligning. This is not correct for diptych dials consisting of a horizontal and vertical dial using a string gnomon between faces, no matter the orientation of the dial faces. Since the string gnomon is continuous, the shadows must meet at the hinge; hence, ''any'' orientation of the dial will show the same time on both dials.
 The Benoy dial was invented by Walter Gordon Benoy of
The Benoy dial was invented by Walter Gordon Benoy of  Invented by the German mathematician Hugo Michnik in 1922, the
Invented by the German mathematician Hugo Michnik in 1922, the  The simplest sundials do not give the hours, but rather note the exact moment of 12:00 noon. In centuries past, such dials were used to set mechanical clocks, which were sometimes so inaccurate as to lose or gain significant time in a single day. The simplest noon-marks have a shadow that passes a mark. Then, an almanac can translate from local solar time and date to civil time. The civil time is used to set the clock. Some noon-marks include a figure-eight that embodies the equation of time, so that no almanac is needed.
In some U.S. colonial-era houses, a noon-mark might be carved into a floor or windowsill. Such marks indicate local noon, and provide a simple and accurate time reference for households to set their clocks. Some Asian countries had post offices set their clocks from a precision noon-mark. These in turn provided the times for the rest of the society. The typical noon-mark sundial was a lens set above an
The simplest sundials do not give the hours, but rather note the exact moment of 12:00 noon. In centuries past, such dials were used to set mechanical clocks, which were sometimes so inaccurate as to lose or gain significant time in a single day. The simplest noon-marks have a shadow that passes a mark. Then, an almanac can translate from local solar time and date to civil time. The civil time is used to set the clock. Some noon-marks include a figure-eight that embodies the equation of time, so that no almanac is needed.
In some U.S. colonial-era houses, a noon-mark might be carved into a floor or windowsill. Such marks indicate local noon, and provide a simple and accurate time reference for households to set their clocks. Some Asian countries had post offices set their clocks from a precision noon-mark. These in turn provided the times for the rest of the society. The typical noon-mark sundial was a lens set above an  *
*