Reuleaux triangle on:
[Wikipedia]
[Google]
[Amazon]
 A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a
A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a
 The Reuleaux triangle may be constructed either directly from three
The Reuleaux triangle may be constructed either directly from three
 The most basic property of the Reuleaux triangle is that it has constant width, meaning that for every pair of parallel supporting lines (two lines of the same slope that both touch the shape without crossing through it) the two lines have the same
The most basic property of the Reuleaux triangle is that it has constant width, meaning that for every pair of parallel supporting lines (two lines of the same slope that both touch the shape without crossing through it) the two lines have the same
pp. 484–485
 Although the Reuleaux triangle has sixfold
Although the Reuleaux triangle has sixfold  Among all
Among all
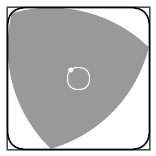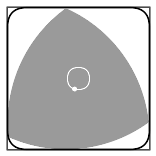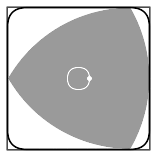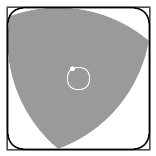 Any curve of constant width can form a rotor within a
Any curve of constant width can form a rotor within a
 Another class of applications of the Reuleaux triangle involves cylindrical objects with a Reuleaux triangle cross section. Several pencils are manufactured in this shape, rather than the more traditional round or hexagonal barrels.. They are usually promoted as being more comfortable or encouraging proper grip, as well as being less likely to roll off tables (since the center of gravity moves up and down more than a rolling hexagon).
A Reuleaux triangle (along with all other curves of constant width) can roll but makes a poor wheel because it does not roll about a fixed center of rotation. An object on top of rollers that have Reuleaux triangle cross-sections would roll smoothly and flatly, but an axle attached to Reuleaux triangle wheels would bounce up and down three times per revolution. This concept was used in a science fiction short story by
Another class of applications of the Reuleaux triangle involves cylindrical objects with a Reuleaux triangle cross section. Several pencils are manufactured in this shape, rather than the more traditional round or hexagonal barrels.. They are usually promoted as being more comfortable or encouraging proper grip, as well as being less likely to roll off tables (since the center of gravity moves up and down more than a rolling hexagon).
A Reuleaux triangle (along with all other curves of constant width) can roll but makes a poor wheel because it does not roll about a fixed center of rotation. An object on top of rollers that have Reuleaux triangle cross-sections would roll smoothly and flatly, but an axle attached to Reuleaux triangle wheels would bounce up and down three times per revolution. This concept was used in a science fiction short story by
 Another class of applications of the Reuleaux triangle involves using it as a part of a
Another class of applications of the Reuleaux triangle involves using it as a part of a
 Many
Many  Following a suggestion of ,. the antennae of the
Following a suggestion of ,. the antennae of the
 According to
According to
 The intersection of four balls of radius ''s'' centered at the vertices of a regular
The intersection of four balls of radius ''s'' centered at the vertices of a regular
films of both types of Meissner body rotating
as well a
It can, however, be made into a surface of constant width, called Reuleaux tetrahedron#Meissner bodies, Meissner's tetrahedron, by replacing three of its edge arcs by curved surfaces, the surfaces of rotation of a circular arc. Alternatively, the
 In the classical presentation of a three-set Venn diagram as three overlapping circles, the central region (representing elements belonging to all three sets) takes the shape of a Reuleaux triangle. The same three circles form one of the standard drawings of the Borromean rings, three mutually linked rings that cannot, however, be realized as geometric circles. Parts of these same circles are used to form the triquetra, a figure of three overlapping semicircles (each two of which form a vesica piscis symbol) that again has a Reuleaux triangle at its center; just as the three circles of the Venn diagram may be interlaced to form the Borromean rings, the three circular arcs of the triquetra may be interlaced to form a trefoil knot.
Relatives of the Reuleaux triangle arise in the problem of finding the minimum perimeter shape that encloses a fixed amount of area and includes three specified points in the plane. For a wide range of choices of the area parameter, the optimal solution to this problem will be a curved triangle whose three sides are circular arcs with equal radii. In particular, when the three points are equidistant from each other and the area is that of the Reuleaux triangle, the Reuleaux triangle is the optimal enclosure.
Circular triangles are triangles with circular-arc edges, including the Reuleaux triangle as well as other shapes.
The deltoid curve is another type of curvilinear triangle, but one in which the curves replacing each side of an equilateral triangle are concave rather than convex. It is not composed of circular arcs, but may be formed by rolling one circle within another of three times the radius. Other planar shapes with three curved sides include the arbelos, which is formed from three semicircles with collinear endpoints, and the Bézier triangle..
The Reuleaux triangle may also be interpreted as the stereographic projection of one spherical triangle, triangular face of a spherical tetrahedron, the Schwarz triangle of parameters with dihedral angle, spherical angles of measure and sides of central angle, spherical length
In the classical presentation of a three-set Venn diagram as three overlapping circles, the central region (representing elements belonging to all three sets) takes the shape of a Reuleaux triangle. The same three circles form one of the standard drawings of the Borromean rings, three mutually linked rings that cannot, however, be realized as geometric circles. Parts of these same circles are used to form the triquetra, a figure of three overlapping semicircles (each two of which form a vesica piscis symbol) that again has a Reuleaux triangle at its center; just as the three circles of the Venn diagram may be interlaced to form the Borromean rings, the three circular arcs of the triquetra may be interlaced to form a trefoil knot.
Relatives of the Reuleaux triangle arise in the problem of finding the minimum perimeter shape that encloses a fixed amount of area and includes three specified points in the plane. For a wide range of choices of the area parameter, the optimal solution to this problem will be a curved triangle whose three sides are circular arcs with equal radii. In particular, when the three points are equidistant from each other and the area is that of the Reuleaux triangle, the Reuleaux triangle is the optimal enclosure.
Circular triangles are triangles with circular-arc edges, including the Reuleaux triangle as well as other shapes.
The deltoid curve is another type of curvilinear triangle, but one in which the curves replacing each side of an equilateral triangle are concave rather than convex. It is not composed of circular arcs, but may be formed by rolling one circle within another of three times the radius. Other planar shapes with three curved sides include the arbelos, which is formed from three semicircles with collinear endpoints, and the Bézier triangle..
The Reuleaux triangle may also be interpreted as the stereographic projection of one spherical triangle, triangular face of a spherical tetrahedron, the Schwarz triangle of parameters with dihedral angle, spherical angles of measure and sides of central angle, spherical length
manhole cover
A manhole cover is a removable plate forming the lid over the opening of a manhole, an opening large enough for a person to pass through that is used as an access point for an underground vault or pipe. It is designed to prevent anyone or anythi ...
be made so that it cannot fall down through the hole?"
They are named after Franz Reuleaux
Franz Reuleaux (; ; 30 September 1829 – 20 August 1905) was a German mechanical engineer and a lecturer at ''Technische Hochschule Berlin'' (today Technische Universität Berlin), later appointed as the president of the academy. He was often c ...
,. a 19th-century German engineer who pioneered the study of machines for translating one type of motion into another, and who used Reuleaux triangles in his designs. However, these shapes were known before his time, for instance by the designers of Gothic church windows, by Leonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested o ...
, who used it for a map projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, ...
, and by Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
in his study of constant-width shapes. Other applications of the Reuleaux triangle include giving the shape to guitar pick
A guitar pick (American English) is a plectrum used for guitars. Picks are generally made of one uniform material, such as some kind of plastic (nylon, Delrin, celluloid), rubber, felt, Tortoiseshell material, tortoiseshell, wood, metal, glass, ...
s, fire hydrant
A fire hydrant, fireplug, firecock (archaic), hydrant riser or Johnny Pump is a connection point by which firefighters can tap into a water supply. It is a component of active fire protection. Underground fire hydrants have been used in Europe a ...
nuts, pencil
A pencil () is a writing or drawing implement with a solid pigment core in a protective casing that reduces the risk of core breakage and keeps it from marking the user's hand.
Pencils create marks by physical abrasion, leaving a trail of ...
s, and drill bit
A drill bit is a cutting tool used in a drill to remove material to create holes, almost always of circular cross-section. Drill bits come in many sizes and shapes and can create different kinds of holes in many different materials. In orde ...
s for drilling filleted square holes, as well as in graphic design in the shapes of some signs and corporate logos.
Among constant-width shapes with a given width, the Reuleaux triangle has the minimum area and the sharpest (smallest) possible angle (120°) at its corners. By several numerical measures it is the farthest from being centrally symmetric
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or ...
. It provides the largest constant-width shape avoiding the points of an integer lattice
In mathematics, the -dimensional integer lattice (or cubic lattice), denoted , is the lattice (group), lattice in the Euclidean space whose lattice points are tuple, -tuples of integers. The two-dimensional integer lattice is also called the s ...
, and is closely related to the shape of the quadrilateral maximizing the ratio of perimeter to diameter. It can perform a complete rotation within a square while at all times touching all four sides of the square, and has the smallest possible area of shapes with this property. However, although it covers most of the square in this rotation process, it fails to cover a small fraction of the square's area, near its corners. Because of this property of rotating within a square, the Reuleaux triangle is also sometimes known as the Reuleaux rotor.
The Reuleaux triangle is the first of a sequence of Reuleaux polygon
In geometry, a Reuleaux polygon is a curve of constant width made up of circular arcs of constant radius. These shapes are named after their prototypical example, the Reuleaux triangle, which in turn is named after 19th-century German engineer ...
s whose boundaries are curves of constant width formed from regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s with an odd number of sides. Some of these curves have been used as the shapes of coins. The Reuleaux triangle can also be generalized into three dimensions in multiple ways: the Reuleaux tetrahedron
The Reuleaux tetrahedron is the intersection of four balls of radius ''s'' centered at the vertices of a regular tetrahedron with side length ''s''. The spherical surface of the ball centered on each vertex passes through the other three verti ...
(the intersection of four balls whose centers lie on a regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
) does not have constant width, but can be modified by rounding its edges to form the Meissner tetrahedron, which does. Alternatively, the surface of revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ...
of the Reuleaux triangle also has constant width.
Construction
circles
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting t ...
, or by rounding the sides of an equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
..
The three-circle construction may be performed with a compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
alone, not even needing a straightedge. By the Mohr–Mascheroni theorem
the same is true more generally of any compass-and-straightedge construction
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
, but the construction for the Reuleaux triangle is particularly simple.
The first step is to mark two arbitrary points of the plane (which will eventually become vertices of the triangle), and use the compass to draw a circle centered at one of the marked points, through the other marked point. Next, one draws a second circle, of the same radius, centered at the other marked point and passing through the first marked point.
Finally, one draws a third circle, again of the same radius, with its center at one of the two crossing points of the two previous circles, passing through both marked points. The central region in the resulting arrangement of three circles will be a Reuleaux triangle.
Alternatively, a Reuleaux triangle may be constructed from an equilateral triangle ''T'' by drawing three arcs of circles, each centered at one vertex of ''T'' and connecting the other two vertices.
Or, equivalently, it may be constructed as the intersection of three disks centered at the vertices of ''T'', with radius equal to the side length of ''T''.
Mathematical properties
Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
from each other, regardless of the orientation of these lines. In any pair of parallel supporting lines, one of the two lines will necessarily touch the triangle at one of its vertices. The other supporting line may touch the triangle at any point on the opposite arc, and their distance (the width of the Reuleaux triangle) equals the radius of this arc..
The first mathematician to discover the existence of curves of constant width, and to observe that the Reuleaux triangle has constant width, may have been Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
.. In a paper that he presented in 1771 and published in 1781 entitled ''De curvis triangularibus'', Euler studied curvilinear
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally inv ...
triangles as well as the curves of constant width, which he called orbiforms.. See in particular section 1.4, "Orbiforms, 1781"pp. 484–485
Extremal measures
By many different measures, the Reuleaux triangle is one of the most extreme curves of constant width. By theBlaschke–Lebesgue theorem
In plane geometry the Blaschke–Lebesgue theorem states that the Reuleaux triangle has the least area of all curves of given constant width. In the form that every curve of a given width has area at least as large as the Reuleaux triangle, it ...
, the Reuleaux triangle has the smallest possible area of any curve of given constant width. This area is
:
where ''s'' is the constant width. One method for deriving this area formula is to partition the Reuleaux triangle into an inner equilateral triangle and three curvilinear regions between this inner triangle and the arcs forming the Reuleaux triangle, and then add the areas of these four sets. At the other extreme, the curve of constant width that has the maximum possible area is a circular disk, which has area .
The angles made by each pair of arcs at the corners of a Reuleaux triangle are all equal to 120°. This is the sharpest possible angle at any vertex of any curve of constant width. Additionally, among the curves of constant width, the Reuleaux triangle is the one with both the largest and the smallest inscribed equilateral triangles. The largest equilateral triangle inscribed in a Reuleaux triangle is the one connecting its three corners, and the smallest one is the one connecting the three midpoint
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
Formula
The midpoint of a segment in ''n''-dim ...
s of its sides. The subset of the Reuleaux triangle consisting of points belonging to three or more diameters is the interior of the larger of these two triangles; it has a larger area than the set of three-diameter points of any other curve of constant width.
dihedral symmetry
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, g ...
, the same as an equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
, it does not have central symmetry
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point (geometry), point is reflected across a designated inversion center, which remains Fixed p ...
.
The Reuleaux triangle is the least symmetric curve of constant width according to two different measures of central asymmetry, the Kovner–Besicovitch measure
In plane geometry the Kovner–Besicovitch measure is a number defined for any bounded convex set describing how close to being central symmetry, centrally symmetric it is. It is the fraction of the area of the set that can be covered by its larges ...
(ratio of area to the largest centrally symmetric
In geometry, a point reflection (also called a point inversion or central inversion) is a geometric transformation of affine space in which every point is reflected across a designated inversion center, which remains fixed. In Euclidean or ...
shape enclosed by the curve) and the Estermann measure (ratio of area to the smallest centrally symmetric shape enclosing the curve). For the Reuleaux triangle, the two centrally symmetric shapes that determine the measures of asymmetry are both hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
al, although the inner one has curved sides.. The Reuleaux triangle has diameters that split its area more unevenly than any other curve of constant width. That is, the maximum ratio of areas on either side of a diameter, another measure of asymmetry, is bigger for the Reuleaux triangle than for other curves of constant width.
Among all shapes of constant width that avoid all points of an integer lattice
In mathematics, the -dimensional integer lattice (or cubic lattice), denoted , is the lattice (group), lattice in the Euclidean space whose lattice points are tuple, -tuples of integers. The two-dimensional integer lattice is also called the s ...
, the one with the largest width is a Reuleaux triangle. It has one of its axes of symmetry parallel to the coordinate axes on a half-integer line. Its width, approximately 1.54, is the root of a degree-6 polynomial with integer coefficients.
Just as it is possible for a circle to be surrounded by six congruent circles that touch it, it is also possible to arrange seven congruent Reuleaux triangles so that they all make contact with a central Reuleaux triangle of the same size. This is the maximum number possible for any curve of constant width.
quadrilateral
In Euclidean geometry, geometry a quadrilateral is a four-sided polygon, having four Edge (geometry), edges (sides) and four Vertex (geometry), corners (vertices). The word is derived from the Latin words ''quadri'', a variant of four, and ''l ...
s, the shape that has the greatest ratio of its perimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
to its diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions a ...
is an equidiagonal kite
A kite is a tethered heavier than air flight, heavier-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. Kites often have ...
that can be inscribed into a Reuleaux triangle.; .
Other measures
By Barbier's theorem all curves of the same constant width including the Reuleaux triangle have equalperimeter
A perimeter is the length of a closed boundary that encompasses, surrounds, or outlines either a two-dimensional shape or a one-dimensional line. The perimeter of a circle or an ellipse is called its circumference.
Calculating the perimet ...
s. In particular this perimeter equals the perimeter of the circle with the same width, which is ..
The radii of the largest inscribed circle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incente ...
of a Reuleaux triangle with width ''s'', and of the circumscribed circle In geometry, a circumscribed circle for a set of points is a circle passing through each of them. Such a circle is said to ''circumscribe'' the points or a polygon formed from them; such a polygon is said to be ''inscribed'' in the circle.
* Circu ...
of the same triangle, are
:
respectively; the sum of these radii equals the width of the Reuleaux triangle. More generally, for every curve of constant width, the largest inscribed circle and the smallest circumscribed circle are concentric, and their radii sum to the constant width of the curve.
The optimal packing density
A packing density or packing fraction of a packing in some space is the fraction of the space filled by the figures making up the packing. In simplest terms, this is the ratio of the volume of bodies in a space to the volume of the space itself. ...
of the Reuleaux triangle in the plane remains unproven, but is conjectured to be
:
which is the density of one possible double lattice packing for these shapes. The best proven upper bound on the packing density is approximately 0.947. It has also been conjectured, but not proven, that the Reuleaux triangles have the highest packing density of any curve of constant width.
Rotation within a square
 Any curve of constant width can form a rotor within a
Any curve of constant width can form a rotor within a square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
, a shape that can perform a complete rotation while staying within the square and at all times touching all four sides of the square. However, the Reuleaux triangle is the rotor with the minimum possible area. As it rotates, its axis does not stay fixed at a single point, but instead follows a curve formed by the pieces of four ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
s. Because of its 120° angles, the rotating Reuleaux triangle cannot reach some points near the sharper angles at the square's vertices, but rather covers a shape with slightly rounded corners, also formed by elliptical arcs.
At any point during this rotation, two of the corners of the Reuleaux triangle touch two adjacent sides of the square, while the third corner of the triangle traces out a curve near the opposite vertex of the square. The shape traced out by the rotating Reuleaux triangle covers approximately 98.8% of the area of the square.
As a counterexample
Reuleaux's original motivation for studying the Reuleaux triangle was as a counterexample, showing that three single-point contacts may not be enough to fix a planar object into a single position. The existence of Reuleaux triangles and other curves of constant width shows that diameter measurements alone cannot verify that an object has a circular cross-section. In connection with theinscribed square problem
The inscribed square problem, also known as the square peg problem or the Toeplitz conjecture, is an unsolved question in geometry: ''Does every plane simple closed curve contain all four vertices of some square?'' This is true if the curve is ...
, observed that the Reuleaux triangle provides an example of a constant-width shape in which no regular polygon with more than four sides can be inscribed, except the regular hexagon, and he described a small modification to this shape that preserves its constant width but also prevents regular hexagons from being inscribed in it. He generalized this result to three dimensions using a cylinder with the same shape as its cross section.
Applications
Reaching into corners
Several types of machinery take the shape of the Reuleaux triangle, based on its property of being able to rotate within a square. The Watts Brothers Tool Works squaredrill bit
A drill bit is a cutting tool used in a drill to remove material to create holes, almost always of circular cross-section. Drill bits come in many sizes and shapes and can create different kinds of holes in many different materials. In orde ...
has the shape of a Reuleaux triangle, modified with concavities to form cutting surfaces. When mounted in a special chuck which allows for the bit not having a fixed centre of rotation, it can drill a hole that is nearly square. (27 page brochure). Although patented by Henry Watts in 1914, similar drills invented by others were used earlier. Other Reuleaux polygons are used to drill pentagonal, hexagonal, and octagonal holes.
Panasonic
is a Japanese multinational electronics manufacturer, headquartered in Kadoma, Osaka, Kadoma, Japan. It was founded in 1918 as in Fukushima-ku, Osaka, Fukushima by Kōnosuke Matsushita. The company was incorporated in 1935 and renamed and c ...
's RULO robotic vacuum cleaner has its shape based on the Reuleaux triangle in order to ease cleaning up dust in the corners of rooms.
Rolling cylinders
Poul Anderson
Poul William Anderson ( ; November 25, 1926 – July 31, 2001) was an American fantasy and science fiction author who was active from the 1940s until his death in 2001. Anderson also wrote historical novels. He won the Hugo Award seven times an ...
titled "The Three-Cornered Wheel". A bicycle with floating axles and a frame supported by the rim of its Reuleaux triangle shaped wheel was built and demonstrated in 2009 by Chinese inventor Guan Baihua, who was inspired by pencils with the same shape.
Mechanism design
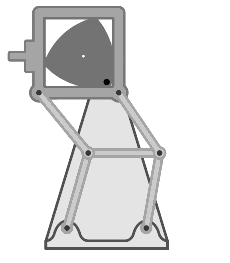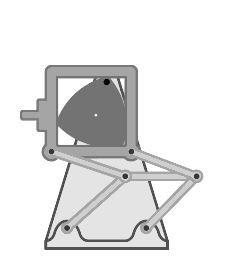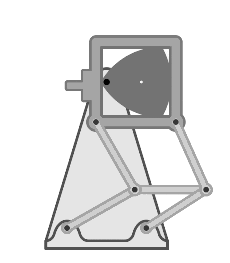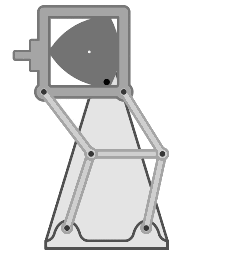
 Another class of applications of the Reuleaux triangle involves using it as a part of a
Another class of applications of the Reuleaux triangle involves using it as a part of a mechanical linkage
A mechanical linkage is an assembly of systems connected so as to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as pro ...
that can convert rotation around a fixed axis
Rotation around a fixed axis or axial rotation is a special case of rotational motion around an ''axis of rotation'' fixed, stationary, or static in three-dimensional space. This type of motion excludes the possibility of the instantaneous axis ...
into reciprocating motion
Reciprocating motion, also called reciprocation, is a repetitive up-and-down or back-and-forth linear motion. It is found in a wide range of mechanisms, including reciprocating engines and pumps. The two opposite motions that comprise a single ...
.. These mechanisms were studied by Franz Reuleaux. With the assistance of the Gustav Voigt company, Reuleaux built approximately 800 models of mechanisms, several of which involved the Reuleaux triangle. Reuleaux used these models in his pioneering scientific investigations of their motion. Although most of the Reuleaux–Voigt models have been lost, 219 of them have been collected at Cornell University
Cornell University is a Private university, private Ivy League research university based in Ithaca, New York, United States. The university was co-founded by American philanthropist Ezra Cornell and historian and educator Andrew Dickson W ...
, including nine based on the Reuleaux triangle.. However, the use of Reuleaux triangles in mechanism design predates the work of Reuleaux; for instance, some steam engine
A steam engine is a heat engine that performs Work (physics), mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a Cylinder (locomotive), cyl ...
s from as early as 1830 had a cam
Cam or CAM may refer to:
Science and technology
* Cam (mechanism), a mechanical linkage which translates motion
* Camshaft, a shaft with a cam
* Camera or webcam, a device that records images or video
In computing
* Computer-aided manufacturin ...
in the shape of a Reuleaux triangle.. Reprinted in .
One application of this principle arises in a film projector
A movie projector (or film projector) is an opto-mechanical device for displaying motion picture film by projecting it onto a screen. Most of the optical and mechanical elements, except for the illumination and sound devices, are present in ...
. In this application, it is necessary to advance the film in a jerky, stepwise motion, in which each frame of film stops for a fraction of a second in front of the projector lens, and then much more quickly the film is moved to the next frame. This can be done using a mechanism in which the rotation of a Reuleaux triangle within a square is used to create a motion pattern for an actuator that pulls the film quickly to each new frame and then pauses the film's motion while the frame is projected.
The rotor of the Wankel engine
The Wankel engine (, ) is a type of internal combustion engine using an eccentric (mechanism), eccentric Pistonless rotary engine, rotary design to convert pressure into rotating motion. The concept was proven by German engineer Felix Wankel, f ...
is shaped as a curvilinear triangle that is often cited as an example of a Reuleaux triangle. However, its curved sides are somewhat flatter than those of a Reuleaux triangle and so it does not have constant width.
Architecture
InGothic architecture
Gothic architecture is an architectural style that was prevalent in Europe from the late 12th to the 16th century, during the High Middle Ages, High and Late Middle Ages, surviving into the 17th and 18th centuries in some areas. It evolved f ...
, beginning in the late 13th century or early 14th century,. the Reuleaux triangle became one of several curvilinear forms frequently used for windows, window tracery
Tracery is an architectural device by which windows (or screens, panels, and vaults) are divided into sections of various proportions by stone ''bars'' or ''ribs'' of moulding. Most commonly, it refers to the stonework elements that support th ...
, and other architectural decorations. For instance, in English Gothic architecture
English Gothic is an architectural style that flourished from the late 12th until the mid-17th century. The style was most prominently used in the construction of Gothic cathedrals and churches, cathedrals and churches. Gothic architecture, Got ...
, this shape was associated with the decorated period, both in its geometric style of 1250–1290 and continuing into its curvilinear style of 1290–1350. It also appears in some of the windows of the Milan Cathedral
Milan Cathedral ( ; ), or Metropolitan Cathedral-Basilica of the Nativity of Saint Mary (), is the cathedral church of Milan, Lombardy, Italy. Dedicated to the Nativity of Mary, Nativity of St. Mary (), it is the seat of the Roman Catholic Archdi ...
. In this context, the shape is sometimes called a ''spherical triangle'', which should not be confused with spherical triangle
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gre ...
meaning a triangle on the surface of a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
. In its use in Gothic church architecture, the three-cornered shape of the Reuleaux triangle may be seen both as a symbol of the Trinity
The Trinity (, from 'threefold') is the Christian doctrine concerning the nature of God, which defines one God existing in three, , consubstantial divine persons: God the Father, God the Son (Jesus Christ) and God the Holy Spirit, thr ...
, and as "an act of opposition to the form of the circle".
The Reuleaux triangle has also been used in other styles of architecture. For instance, Leonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 1452 - 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested o ...
sketched this shape as the plan for a fortification.. Modern buildings that have been claimed to use a Reuleaux triangle shaped floorplan include the MIT Kresge Auditorium, the Kölntriangle, the Donauturm, the Torre de Collserola, and the Mercedes-Benz Museum
The Mercedes-Benz Museum is an automobile museum in Stuttgart, Germany. It covers the history of the Mercedes-Benz brand and the brands associated with it. Stuttgart is home to the Mercedes-Benz brand and the international headquarters of the Merc ...
. However in many cases these are merely rounded triangles, with different geometry than the Reuleaux triangle.
Mapmaking
Another early application of the Reuleaux triangle, da Vinci's world map from circa 1514, was aworld map
A world map is a map of most or all of the surface of Earth. World maps, because of their scale, must deal with the problem of projection. Maps rendered in two dimensions by necessity distort the display of the three-dimensional surface of t ...
in which the spherical surface of the earth was divided into eight octants, each flattened into the shape of a Reuleaux triangle...
Similar maps also based on the Reuleaux triangle were published by Oronce Finé
Oronce Fine (or Finé; Latin: ''Orontius Finnaeus'' or ''Finaeus''; ; 20 December 1494 – 8 August 1555) was a French mathematician, cartographer, editor and book illustrator.
Life
Born in Briançon, the son and grandson of physicians, he was e ...
in 1551 and by John Dee
John Dee (13 July 1527 – 1608 or 1609) was an English mathematician, astronomer, teacher, astrologer, occultist, and alchemist. He was the court astronomer for, and advisor to, Elizabeth I, and spent much of his time on alchemy, divination, ...
in 1580.
Other objects
guitar pick
A guitar pick (American English) is a plectrum used for guitars. Picks are generally made of one uniform material, such as some kind of plastic (nylon, Delrin, celluloid), rubber, felt, Tortoiseshell material, tortoiseshell, wood, metal, glass, ...
s employ the Reuleaux triangle, as its shape combines a sharp point to provide strong articulation, with a wide tip to produce a warm timbre. Because all three points of the shape are usable, it is easier to orient and wears less quickly compared to a pick with a single tip..
The Reuleaux triangle has been used as the shape for the cross section of a fire hydrant
A fire hydrant, fireplug, firecock (archaic), hydrant riser or Johnny Pump is a connection point by which firefighters can tap into a water supply. It is a component of active fire protection. Underground fire hydrants have been used in Europe a ...
valve nut. The constant width of this shape makes it difficult to open the fire hydrant using standard parallel-jawed wrenches; instead, a wrench with a special shape is needed. This property allows the fire hydrants to be opened only by firefighters (who have the special wrench) and not by other people trying to use the hydrant as a source of water for other activities.
 Following a suggestion of ,. the antennae of the
Following a suggestion of ,. the antennae of the Submillimeter Array
The Submillimeter Array (SMA) consists of eight diameter radio telescopes arranged as an interferometer for submillimetre astronomy, submillimeter wavelength observations. It is the first purpose-built submillimeter interferometer, constructed a ...
, a radio-wave astronomical observatory on Mauna Kea
Mauna Kea (, ; abbreviation for ''Mauna a Wākea''); is a dormant Shield volcano, shield volcano on the Hawaii (island), island of Hawaii. Its peak is above sea level, making it the List of U.S. states by elevation, highest point in Hawaii a ...
in Hawaii
Hawaii ( ; ) is an island U.S. state, state of the United States, in the Pacific Ocean about southwest of the U.S. mainland. One of the two Non-contiguous United States, non-contiguous U.S. states (along with Alaska), it is the only sta ...
, are arranged on four nested Reuleaux triangles... Placing the antennae on a curve of constant width causes the observatory to have the same spatial resolution in all directions, and provides a circular observation beam. As the most asymmetric curve of constant width, the Reuleaux triangle leads to the most uniform coverage of the plane for the Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
of the signal from the array. The antennae may be moved from one Reuleaux triangle to another for different observations, according to the desired angular resolution of each observation. The precise placement of the antennae on these Reuleaux triangles was optimized using a neural network
A neural network is a group of interconnected units called neurons that send signals to one another. Neurons can be either biological cells or signal pathways. While individual neurons are simple, many of them together in a network can perfor ...
. In some places the constructed observatory departs from the preferred Reuleaux triangle shape because that shape was not possible within the given site.
Signs and logos
The shield shapes used for many signs and corporate logos feature rounded triangles. However, only some of these are Reuleaux triangles. The corporate logo of Petrofina (Fina), a Belgian oil company with major operations in Europe, North America and Africa, used a Reuleaux triangle with the Fina name from 1950 until Petrofina's merger with ''Total S.A.'' (todayTotalEnergies
TotalEnergies SE is a French multinational integrated energy and petroleum company founded in 1924 and is one of the seven supermajor oil companies. Its businesses cover the entire oil and gas chain, from crude oil and natural gas explorati ...
) in 2000.
Another corporate logo framed in the Reuleaux triangle, the south-pointing compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself with No ...
of Bavaria Brewery, was part of a makeover by design company Total Identity that won the SAN 2010 Advertiser of the Year award. The Reuleaux triangle is also used in the logo of Colorado School of Mines
The Colorado School of Mines (Mines) is a public research university in Golden, Colorado, United States. Founded in 1874, the school offers both undergraduate and graduate degrees in engineering, science, and mathematics, with a focus on ener ...
.
In the United States, the National Trails System
The National Trails System is a series of trails in the United States designated "to promote the preservation of, public access to, travel within, and enjoyment and appreciation of the open-air, outdoor areas and historic resources of the Nati ...
and United States Bicycle Route System both mark routes with Reuleaux triangles on signage.
In nature
Plateau's laws
Plateau's laws describe the structure of soap films. These laws were formulated in the 19th century by the Belgian physicist Joseph Plateau from his experimental observations. Many patterns in nature are based on foams obeying these laws.
Laws ...
, the circular arcs in two-dimensional soap bubble
A soap bubble (commonly referred to as simply a bubble) is an extremely thin soap film, film of soap or detergent and water enclosing air that forms a hollow sphere with an iridescent surface. Soap bubbles usually last for only a few seconds b ...
clusters meet at 120° angles, the same angle found at the corners of a Reuleaux triangle. Based on this fact, it is possible to construct clusters in which some of the bubbles take the form of a Reuleaux triangle..
The shape was first isolated in crystal form in 2014 as Reuleaux triangle disks. Basic bismuth nitrate disks with the Reuleaux triangle shape were formed from the hydrolysis
Hydrolysis (; ) is any chemical reaction in which a molecule of water breaks one or more chemical bonds. The term is used broadly for substitution reaction, substitution, elimination reaction, elimination, and solvation reactions in which water ...
and precipitation
In meteorology, precipitation is any product of the condensation of atmospheric water vapor that falls from clouds due to gravitational pull. The main forms of precipitation include drizzle, rain, rain and snow mixed ("sleet" in Commonwe ...
of bismuth nitrate in an ethanol–water system in the presence of 2,3-bis(2-pyridyl)pyrazine.
Generalizations
Triangular curves of constant width with smooth rather than sharp corners may be obtained as the locus of points at a fixed distance from the Reuleaux triangle. Other generalizations of the Reuleaux triangle include surfaces in three dimensions, curves of constant width with more than three sides, and the Yanmouti sets which provide extreme examples of an inequality between width, diameter, and inradius.Three-dimensional version
 The intersection of four balls of radius ''s'' centered at the vertices of a regular
The intersection of four balls of radius ''s'' centered at the vertices of a regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
with side length ''s'' is called the Reuleaux tetrahedron
The Reuleaux tetrahedron is the intersection of four balls of radius ''s'' centered at the vertices of a regular tetrahedron with side length ''s''. The spherical surface of the ball centered on each vertex passes through the other three verti ...
, but its surface is not a surface of constant width. Weber also hafilms of both types of Meissner body rotating
as well a
It can, however, be made into a surface of constant width, called Reuleaux tetrahedron#Meissner bodies, Meissner's tetrahedron, by replacing three of its edge arcs by curved surfaces, the surfaces of rotation of a circular arc. Alternatively, the
surface of revolution
A surface of revolution is a Surface (mathematics), surface in Euclidean space created by rotating a curve (the ''generatrix'') one full revolution (unit), revolution around an ''axis of rotation'' (normally not Intersection (geometry), intersec ...
of a Reuleaux triangle through one of its symmetry axes forms a surface of constant width, with minimum volume among all known surfaces of revolution of given constant width..
Reuleaux polygons
The Reuleaux triangle can be generalized to regular or irregular polygons with an odd number of sides, yielding aReuleaux polygon
In geometry, a Reuleaux polygon is a curve of constant width made up of circular arcs of constant radius. These shapes are named after their prototypical example, the Reuleaux triangle, which in turn is named after 19th-century German engineer ...
, a curve of constant width formed from circular arcs of constant radius. The constant width of these shapes allows their use as coins that can be used in coin-operated machines. Although coins of this type in general circulation usually have more than three sides, a Reuleaux triangle has been used for a commemorative coin from Bermuda.
Similar methods can be used to enclose an arbitrary simple polygon within a curve of constant width, whose width equals the diameter of the given polygon. The resulting shape consists of circular arcs (at most as many as sides of the polygon), can be constructed algorithmically in linear time, and can be drawn with compass and straightedge. Although the Reuleaux polygons all have an odd number of circular-arc sides, it is possible to construct constant-width shapes with an even number of circular-arc sides of varying radii.
Yanmouti sets
The Yanmouti sets are defined as the convex hulls of an equilateral triangle together with three circular arcs, centered at the triangle vertices and spanning the same angle as the triangle, with equal radii that are at most equal to the side length of the triangle. Thus, when the radius is small enough, these sets degenerate to the equilateral triangle itself, but when the radius is as large as possible they equal the corresponding Reuleaux triangle. Every shape with width ''w'', diameter ''d'', and inradius ''r'' (the radius of the largest possible circle contained in the shape) obeys the inequality : and this inequality becomes an equality for the Yanmouti sets, showing that it cannot be improved.Related figures
References
External links
*{{mathworld, id=ReuleauxTriangle, title=Reuleaux Triangle, mode=cs2 Piecewise-circular curves Types of triangles Constant width Eponymous geometric shapes