Non-analytic smooth function on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, smooth functions (also called infinitely
/nowiki>0, 1 /nowiki>''a'', ''b'' /nowiki>''b'', ''c''
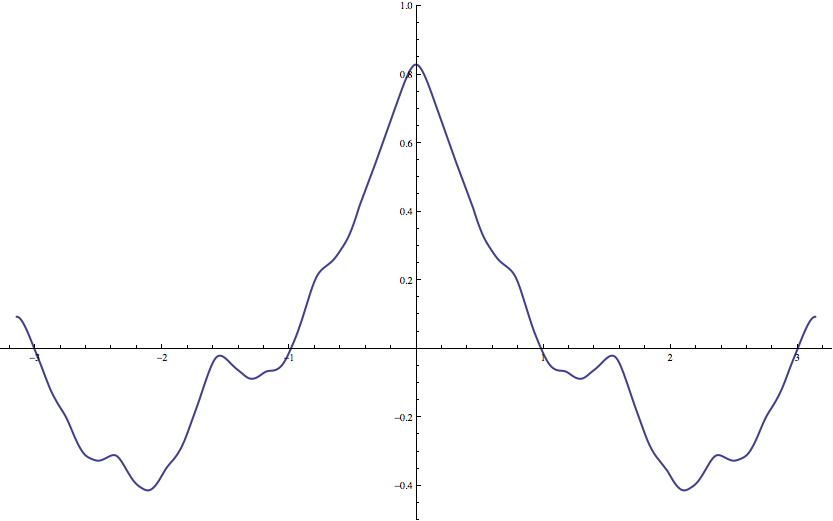 A more
A more
/nowiki>−1,1 /nowiki>−1,1
 For every radius ''r'' > 0,
:
with Euclidean norm , , ''x'', , defines a smooth function on ''n''-dimensional
For every radius ''r'' > 0,
:
with Euclidean norm , , ''x'', , defines a smooth function on ''n''-dimensional
differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its ...
functions) and analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex ...
s are two very important types of functions. One can easily prove that any analytic function of a real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010) ...
argument is smooth. The converse
Converse may refer to:
Mathematics and logic
* Converse (logic), the result of reversing the two parts of a definite or implicational statement
** Converse implication, the converse of a material implication
** Converse nonimplication, a logical c ...
is not true, as demonstrated with the counterexample
A counterexample is any exception to a generalization. In logic a counterexample disproves the generalization, and does so rigorously in the fields of mathematics and philosophy. For example, the fact that "John Smith is not a lazy student" is a ...
below.
One of the most important applications of smooth functions with compact support is the construction of so-called mollifier
In mathematics, mollifiers (also known as ''approximations to the identity'') are smooth functions with special properties, used for example in distribution theory to create sequences of smooth functions approximating nonsmooth (generalized) f ...
s, which are important in theories of generalized function
In mathematics, generalized functions are objects extending the notion of functions. There is more than one recognized theory, for example the theory of distributions. Generalized functions are especially useful in making discontinuous functions ...
s, such as Laurent Schwartz's theory of distributions.
The existence of smooth but non-analytic functions represents one of the main differences between differential geometry and analytic geometry. In terms of sheaf theory
In mathematics, a sheaf is a tool for systematically tracking data (such as sets, abelian groups, rings) attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could ...
, this difference can be stated as follows: the sheaf of differentiable functions on a differentiable manifold is fine, in contrast with the analytic case.
The functions below are generally used to build up partitions of unity
In mathematics, a partition of unity of a topological space is a set of continuous functions from to the unit interval ,1such that for every point x\in X:
* there is a neighbourhood of where all but a finite number of the functions of are 0, ...
on differentiable manifolds.
An example function
Definition of the function
Consider the function : defined for everyreal number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
''x''.
The function is smooth
The function ''f'' has continuousderivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. ...
s of all orders at every point ''x'' of the real line. The formula for these derivatives is
:
where ''pn''(''x'') is a polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example ...
of degree ''n'' − 1 given recursively
Recursion (adjective: ''recursive'') occurs when a thing is defined in terms of itself or of its type. Recursion is used in a variety of disciplines ranging from linguistics to logic. The most common application of recursion is in mathematics ...
by ''p''1(''x'') = 1 and
:
for any positive integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
''n''. From this formula, it is not completely clear that the derivatives are continuous at 0; this follows from the one-sided limit
In calculus, a one-sided limit refers to either one of the two limits of a function f(x) of a real variable x as x approaches a specified point either from the left or from the right.
The limit as x decreases in value approaching a (x approach ...
:
for any nonnegative
In mathematics, the sign of a real number is its property of being either positive, negative, or zero. Depending on local conventions, zero may be considered as being neither positive nor negative (having no sign or a unique third sign), or it ...
integer ''m''.
By the power series representation of the exponential function, we have for every natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''cardinal ...
(including zero)
:
because all the positive terms for are added. Therefore, dividing this inequality by and taking the limit from above,
:
We now prove the formula for the ''n''th derivative of ''f'' by mathematical induction
Mathematical induction is a method for proving that a statement ''P''(''n'') is true for every natural number ''n'', that is, that the infinitely many cases ''P''(0), ''P''(1), ''P''(2), ''P''(3), ... all hold. Informal metaphors help ...
. Using the chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
, the reciprocal rule
In calculus, the reciprocal rule gives the derivative of the reciprocal of a function ''f'' in terms of the derivative of ''f''. The reciprocal rule can be used to show that the power rule holds for negative exponents if it has already been e ...
, and the fact that the derivative of the exponential function is again the exponential function, we see that the formula is correct for the first derivative of ''f'' for all ''x'' > 0 and that ''p''1(''x'') is a polynomial of degree 0. Of course, the derivative of ''f'' is zero for ''x'' < 0.
It remains to show that the right-hand side derivative of ''f'' at ''x'' = 0 is zero. Using the above limit, we see that
:
The induction step from ''n'' to ''n'' + 1 is similar. For ''x'' > 0 we get for the derivative
:
where ''p''''n''+1(''x'') is a polynomial of degree ''n'' = (''n'' + 1) − 1. Of course, the (''n'' + 1)st derivative of ''f'' is zero for ''x'' < 0. For the right-hand side derivative of ''f'' (''n'') at ''x'' = 0 we obtain with the above limit
:
The function is not analytic
As seen earlier, the function ''f'' is smooth, and all its derivatives at theorigin
Origin(s) or The Origin may refer to:
Arts, entertainment, and media
Comics and manga
* ''Origin'' (comics), a Wolverine comic book mini-series published by Marvel Comics in 2002
* ''The Origin'' (Buffy comic), a 1999 ''Buffy the Vampire Sl ...
are 0. Therefore, the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
of ''f'' at the origin converges everywhere to the zero function
0 (zero) is a number representing an empty quantity. In place-value notation such as the Hindu–Arabic numeral system, 0 also serves as a placeholder numerical digit, which works by multiplying digits to the left of 0 by the radix, usual ...
,
:
and so the Taylor series does not equal ''f''(''x'') for ''x'' > 0. Consequently, ''f'' is not analytic at the origin.
Smooth transition functions
The function : has a strictly positive denominator everywhere on the real line, hence ''g'' is also smooth. Furthermore, ''g''(''x'') = 0 for ''x'' ≤ 0 and ''g''(''x'') = 1 for ''x'' ≥ 1, hence it provides a smooth transition from the level 0 to the level 1 in theunit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1. It is often denoted ' (capital letter ). In addition to its role in real analysis ...
bump function
In mathematics, a bump function (also called a test function) is a function f: \R^n \to \R on a Euclidean space \R^n which is both smooth (in the sense of having continuous derivatives of all orders) and compactly supported. The set of all bum ...
.
A smooth function which is nowhere real analytic
 A more
A more pathological
Pathology is the study of the causes and effects of disease or injury. The word ''pathology'' also refers to the study of disease in general, incorporating a wide range of biology research fields and medical practices. However, when used in th ...
example is an infinitely differentiable function which is not analytic ''at any point''. It can be constructed by means of a Fourier series as follows. Define for all
:
Since the series converges for all , this function is easily seen to be of class C∞, by a standard inductive application of the Weierstrass M-test
In mathematics, the Weierstrass M-test is a test for determining whether an infinite series of functions converges uniformly and absolutely. It applies to series whose terms are bounded functions with real or complex values, and is analogous t ...
to demonstrate uniform convergence
In the mathematical field of analysis, uniform convergence is a mode of convergence of functions stronger than pointwise convergence. A sequence of functions (f_n) converges uniformly to a limiting function f on a set E if, given any arbitrarily ...
of each series of derivatives.
We now show that is not analytic at any dyadic rational multiple of π, that is, at any with and . Since the sum of the first terms is analytic, we need only consider , the sum of the terms with . For all orders of derivation with , and we have
:
where we used the fact that for all , and we bounded the first sum from below by the term with . As a consequence, at any such
:
so that the radius of convergence
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or \infty. When it is positive, the power series ...
of the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
of at is 0 by the Cauchy-Hadamard formula. Since the set of analyticity of a function is an open set, and since dyadic rationals are dense
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically ...
, we conclude that , and hence , is nowhere analytic in .
Application to Taylor series
For every sequence α0, α1, α2, . . . of real or complex numbers, the following construction shows the existence of a smooth function ''F'' on the real line which has these numbers as derivatives at the origin. In particular, every sequence of numbers can appear as the coefficients of theTaylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
of a smooth function. This result is known as Borel's lemma, after Émile Borel
Félix Édouard Justin Émile Borel (; 7 January 1871 – 3 February 1956) was a French mathematician and politician. As a mathematician, he was known for his founding work in the areas of measure theory and probability.
Biography
Borel was ...
.
With the smooth transition function ''g'' as above, define
:
This function ''h'' is also smooth; it equals 1 on the closed interval monomial
In mathematics, a monomial is, roughly speaking, a polynomial which has only one term. Two definitions of a monomial may be encountered:
# A monomial, also called power product, is a product of powers of variables with nonnegative integer expone ...
''xn'' on supremum norm
In mathematical analysis, the uniform norm (or ) assigns to real- or complex-valued bounded functions defined on a set the non-negative number
:\, f\, _\infty = \, f\, _ = \sup\left\.
This norm is also called the , the , the , or, when th ...
of ''ψn'' and its first ''n'' derivatives, are well-defined real numbers. Define the scaled functions
:
By repeated application of the chain rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , ...
,
:
and, using the previous result for the ''k''-th derivative of ''ψn'' at zero,
:
It remains to show that the function
:
is well defined and can be differentiated term-by-term infinitely many times.See e.g. Chapter V, Section 2, Theorem 2.8 and Corollary 2.9 about the differentiability of the limits of sequences of functions in To this end, observe that for every ''k''
:
where the remaining infinite series converges by the ratio test
In mathematics, the ratio test is a test (or "criterion") for the convergence of a series
:\sum_^\infty a_n,
where each term is a real or complex number and is nonzero when is large. The test was first published by Jean le Rond d'Alembert a ...
.
Application to higher dimensions
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
with support in the ball of radius ''r'', but .
Complex analysis
This pathology cannot occur with differentiable functions of a complex variable rather than of a real variable. Indeed, all holomorphic functions are analytic, so that the failure of the function ''f'' defined in this article to be analytic in spite of its being infinitely differentiable is an indication of one of the most dramatic differences between real-variable and complex-variable analysis. Note that although the function ''f'' has derivatives of all orders over the real line, theanalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of definition of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a n ...
of ''f'' from the positive half-line ''x'' > 0 to the complex plane, that is, the function
:
has an essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits odd behavior.
The category ''essential singularity'' is a "left-over" or default group of isolated singularities that a ...
at the origin, and hence is not even continuous, much less analytic. By the great Picard theorem, it attains every complex value (with the exception of zero) infinitely many times in every neighbourhood of the origin.
See also
*Bump function
In mathematics, a bump function (also called a test function) is a function f: \R^n \to \R on a Euclidean space \R^n which is both smooth (in the sense of having continuous derivatives of all orders) and compactly supported. The set of all bum ...
* Fabius function
* Flat function
* Mollifier
In mathematics, mollifiers (also known as ''approximations to the identity'') are smooth functions with special properties, used for example in distribution theory to create sequences of smooth functions approximating nonsmooth (generalized) f ...
Notes
External links
* {{planetmath reference, urlname=InfinitelydifferentiableFunctionThatIsNotAnalytic, title=Infinitely-differentiable function that is not analytic Smooth functions Articles containing proofs