Multivariate kernel density estimation

Kernel density estimation is a nonparametric technique for density estimation i.e., estimation of probability density functions, which is one of the fundamental questions in statistics. It can be viewed as a generalisation of histogram density estimation with improved statistical properties. Apart from histograms, other types of density estimators include parametric, spline, wavelet and Fourier series. Kernel density estimators were first introduced in the scientific literature for univariate data in the 1950s and 1960s and subsequently have been widely adopted. It was soon recognised that analogous estimators for multivariate data would be an important addition to multivariate statistics. Based on research carried out in the 1990s and 2000s, multivariate kernel density estimation has reached a level of maturity comparable to its univariate counterparts.

Motivation

We take an illustrative synthetic bivariate data set of 50 points to illustrate the construction of histograms. This requires the choice of an anchor point (the lower left corner of the histogram grid). For the histogram on the left, we choose (−1.5, −1.5): for the one on the right, we shift the anchor point by 0.125 in both directions to (−1.625, −1.625). Both histograms have a binwidth of 0.5, so any differences are due to the change in the anchor point only. The colour-coding indicates the number of data points which fall into a bin: 0=white, 1=pale yellow, 2=bright yellow, 3=orange, 4=red. The left histogram appears to indicate that the upper half has a higher density than the lower half, whereas the reverse is the case for the right-hand histogram, confirming that histograms are highly sensitive to the placement of the anchor point.

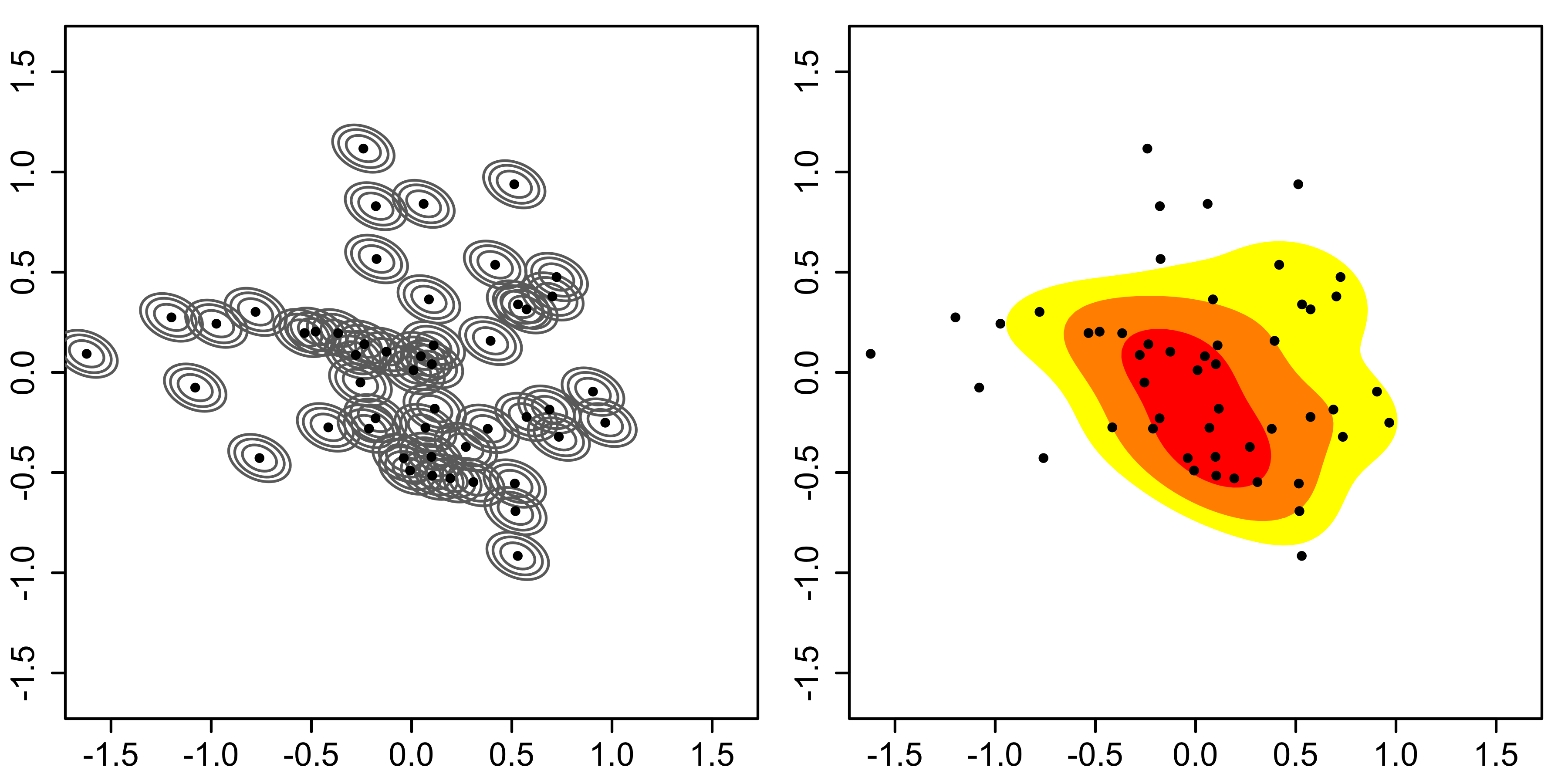
One possible solution to this anchor point placement problem is to remove the histogram binning grid completely. In the left figure below, a kernel (represented by the grey lines) is centred at each of the 50 data points above. The result of summing these kernels is given on the right figure, which is a kernel density estimate. The most striking difference between kernel density estimates and histograms is that the former are easier to interpret since they do not contain artifices induced by a binning grid.
The coloured contours correspond to the smallest region which contains the respective probability mass: red = 25%, orange + red = 50%, yellow + orange + red = 75%, thus indicating that a single central region contains the highest density.

The goal of density estimation is to take a finite sample of data and to make inferences about the underlying probability density function everywhere, including where no data are observed. In kernel density estimation, the contribution of each data point is smoothed out from a single point into a region of space surrounding it. Aggregating the individually smoothed contributions gives an overall picture of the structure of the data and its density function. In the details to follow, we show that this approach leads to a reasonable estimate of the underlying density function.

Definition

The previous figure is a graphical representation of kernel density estimate, which we now define in an exact manner. Let x₁, x₂, ..., x_''n'' be a sample of ''d''-variate random vectors drawn from a common distribution described by the density function ''ƒ''. The kernel density estimate is defined to be
: $\hat_\mathbf(\mathbf)= \frac1n \sum_^n K_\mathbf (\mathbf - \mathbf_i)$
where
* , are ''d''-vectors;
* H is the bandwidth (or smoothing) ''d×d'' matrix which is symmetric and positive definite;
* ''K'' is the kernel function which is a symmetric multivariate density;
* $K_\mathbf(\mathbf)=, \mathbf, ^K(\mathbf^\mathbf )$.

The choice of the kernel function ''K'' is not crucial to the accuracy of kernel density estimators, so we use the standard multivariate normal kernel throughout: $K_\mathbf(\mathbf)= \mathbf^ e^$, where H plays the role of the covariance matrix. On the other hand, the choice of the bandwidth matrix H is the single most important factor affecting its accuracy since it controls the amount and orientation of smoothing induced. That the bandwidth matrix also induces an orientation is a basic difference between multivariate kernel density estimation from its univariate analogue since orientation is not defined for 1D kernels. This leads to the choice of the parametrisation of this bandwidth matrix. The three main parametrisation classes (in increasing order of complexity) are ''S'', the class of positive scalars times the identity matrix; ''D'', diagonal matrices with positive entries on the main diagonal; and ''F'', symmetric positive definite matrices. The ''S'' class kernels have the same amount of smoothing applied in all coordinate directions, ''D'' kernels allow different amounts of smoothing in each of the coordinates, and ''F'' kernels allow arbitrary amounts and orientation of the smoothing. Historically ''S'' and ''D'' kernels are the most widespread due to computational reasons, but research indicates that important gains in accuracy can be obtained using the more general ''F'' class kernels.

Optimal bandwidth matrix selection

The most commonly used optimality criterion for selecting a bandwidth matrix is the MISE or mean integrated squared error

: \operatorname (\mathbf) = \operatorname\!\left , \int (\hat_\mathbf (\mathbf) - f(\mathbf))^2 \, d\mathbf \;\right

This in general does not possess a closed-form expression, so it is usual to use its asymptotic approximation (AMISE) as a proxy

: $\operatorname (\mathbf) = n^ , \mathbf, ^ R(K) + \tfrac m_2(K)^2 (\operatorname^T \mathbf) \mathbf_4 (\operatorname \mathbf)$

where
* $R(K) = \int K(\mathbf)^2 \, d\mathbf$, with when ''K'' is a normal kernel
* $\int \mathbf \mathbf^T K(\mathbf) \, d\mathbf = m_2(K) \mathbf_d$,
:with I_d being the ''d × d'' identity matrix, with ''m''₂ = 1 for the normal kernel
* D²''ƒ'' is the ''d × d'' Hessian matrix of second order partial derivatives of ''ƒ''
* $\mathbf_4 = \int (\operatorname \, \operatorname^2 f(\mathbf)) (\operatorname^T \operatorname^2 f(\mathbf)) \, d\mathbf$ is a ''d''² × ''d''² matrix of integrated fourth order partial derivatives of ''ƒ''
* vec is the vector operator which stacks the columns of a matrix into a single vector e.g. $\operatorname\begina & c \\ b & d\end = \begina & b & c & d\end^T.$

The quality of the AMISE approximation to the MISE is given by

: $\operatorname (\mathbf) = \operatorname (\mathbf) + o(n^ , \mathbf, ^ + \operatorname \, \mathbf^2)$

where ''o'' indicates the usual small o notation. Heuristically this statement implies that the AMISE is a 'good' approximation of the MISE as the sample size n → ∞.

It can be shown that any reasonable bandwidth selector H has H = ''O''(''n''^{−2/(''d''+4)}) where the big O notation is applied elementwise. Substituting this into the MISE formula yields that the optimal MISE is ''O''(''n''^{−4/(''d''+4)}). Thus as ''n'' → ∞, the MISE → 0, i.e. the kernel density estimate converges in mean square and thus also in probability to the true density ''f''. These modes of convergence are confirmation of the statement in the motivation section that kernel methods lead to reasonable density estimators. An ideal optimal bandwidth selector is

: $\mathbf_ = \operatorname_ \, \operatorname (\mathbf).$

Since this ideal selector contains the unknown density function ''ƒ'', it cannot be used directly. The many different varieties of data-based bandwidth selectors arise from the different estimators of the AMISE. We concentrate on two classes of selectors which have been shown to be the most widely applicable in practice: smoothed cross validation and plug-in selectors.

Plug-in

The plug-in (PI) estimate of the AMISE is formed by replacing Ψ₄ by its estimator $\hat_4$

: $\operatorname(\mathbf) = n^ , \mathbf, ^ R(K) + \tfrac m_2(K)^2 (\operatorname^T \mathbf) \hat_4 (\mathbf) (\operatorname \, \mathbf)$

where \hat_4 (\mathbf) = n^ \sum_^n
\sum_^n \operatorname \, \operatorname^2) (\operatorname^T \operatorname^2)K_\mathbf (\mathbf_i - \mathbf_j). Thus $\hat_ = \operatorname_ \, \operatorname (\mathbf)$ is the plug-in selector. These references also contain algorithms on optimal estimation of the pilot bandwidth matrix G and establish that $\hat_$ converges in probability to H_AMISE.

Smoothed cross validation

Smoothed cross validation (SCV) is a subset of a larger class of cross validation techniques. The SCV estimator differs from the plug-in estimator in the second term

: $\operatorname(\mathbf) = n^ , \mathbf, ^ R(K) + n^ \sum_^n \sum_^n (K_ - 2K_ + K_) (\mathbf_i - \mathbf_j)$

Thus $\hat_ = \operatorname_ \, \operatorname (\mathbf)$ is the SCV selector.
These references also contain algorithms on optimal estimation of the pilot bandwidth matrix G and establish that $\hat_$ converges in probability to H_AMISE.

Rule of thumb

Silverman's rule of thumb suggests using $\sqrt = \left(\frac\right)^ n^ \sigma_i$, where $\sigma_i$ is the standard deviation of the ith variable and $d$ is the number of dimensions, and $\mathbf_ = 0, i\neq j$. Scott's rule is $\sqrt = n^ \sigma_i$.

Asymptotic analysis

In the optimal bandwidth selection section, we introduced the MISE. Its construction relies on the expected value and the variance of the density estimator

:$\operatorname \hat(\mathbf;\mathbf) = K_\mathbf * f (\mathbf) = f(\mathbf) + \frac m_2(K)\operatorname (\mathbf \operatorname^2 f(\mathbf)) + o(\operatorname \, \mathbf)$

where * is the convolution operator between two functions, and

:$\operatorname \hat(\mathbf;\mathbf) = n^ , \mathbf, ^ R(K)f(\mathbf x) + o(n^ , \mathbf, ^).$

For these two expressions to be well-defined, we require that all elements of H tend to 0 and that ''n''⁻¹ , H, ^−1/2 tends to 0 as ''n'' tends to infinity. Assuming these two conditions, we see that the expected value tends to the true density ''f'' i.e. the kernel density estimator is asymptotically unbiased; and that the variance tends to zero. Using the standard mean squared value decomposition

:\operatorname \, \hat(\mathbf;\mathbf) = \operatorname \hat(\mathbf;\mathbf) + operatorname \hat(\mathbf;\mathbf) - f(\mathbf)2

we have that the MSE tends to 0, implying that the kernel density estimator is (mean square) consistent and hence converges in probability to the true density ''f''. The rate of convergence of the MSE to 0 is the necessarily the same as the MISE rate noted previously ''O''(''n''^−4/(d+4)), hence the covergence rate of the density estimator to ''f'' is ''O_p''(n^{−2/(''d''+4)}) where ''O_p'' denotes order in probability. This establishes pointwise convergence. The functional covergence is established similarly by considering the behaviour of the MISE, and noting that under sufficient regularity, integration does not affect the convergence rates.

For the data-based bandwidth selectors considered, the target is the AMISE bandwidth matrix. We say that a data-based selector converges to the AMISE selector at relative rate ''O_p''(''n''^−''α''), ''α'' > 0 if

:$\operatorname (\hat - \mathbf_) = O(n^) \operatorname \mathbf_.$

It has been established that the plug-in and smoothed cross validation selectors (given a single pilot bandwidth G) both converge at a relative rate of ''O_p''(''n''^{−2/(''d''+6)}) i.e., both these data-based selectors are consistent estimators.

Density estimation with a full bandwidth matrix

Th
ks package
in R implements the plug-in and smoothed cross validation selectors (amongst others). This dataset (included in the base distribution of R) contains
272 records with two measurements each: the duration time of an eruption (minutes) and the
waiting time until the next eruption (minutes) of the Old Faithful Geyser in Yellowstone National Park, USA.

The code fragment computes the kernel density estimate with the plug-in bandwidth matrix $\hat_ = \begin0.052 & 0.510 \\ 0.510 & 8.882\end.$ Again, the coloured contours correspond to the smallest region which contains the respective probability mass: red = 25%, orange + red = 50%, yellow + orange + red = 75%. To compute the SCV selector, Hpi is replaced with Hscv. This is not displayed here since it is mostly similar to the plug-in estimate for this example.

library(ks)
data(faithful)
H <- Hpi(x=faithful)
fhat <- kde(x=faithful, H=H)
plot(fhat, display="filled.contour2")
points(faithful, cex=0.5, pch=16)

Density estimation with a diagonal bandwidth matrix

We consider estimating the density of the Gaussian mixture
,
from 500 randomly generated points. We employ the Matlab routine fo
2-dimensional data

The routine is an automatic bandwidth selection method specifically designed
for a second order Gaussian kernel.
The figure shows the joint density estimate that results from using the automatically selected bandwidth.

Matlab script for the example

Type the following commands in Matlab afte
downloading
and saving the function kde2d.m
in the current directory.

clear all
% generate synthetic data
data= andn(500,2);
randn(500,1)+3.5, randn(500,1);
% call the routine, which has been saved in the current directory
andwidth,density,X,Ykde2d(data);
% plot the data and the density estimate
contour3(X,Y,density,50), hold on
plot(data(:,1),data(:,2),'r.','MarkerSize',5)

Alternative optimality criteria

The MISE is the expected integrated ''L₂'' distance between the density estimate and the true density function ''f''. It is the most widely used, mostly due to its tractability and most software implement MISE-based bandwidth selectors.
There are alternative optimality criteria, which attempt to cover cases where MISE is not an appropriate measure. The equivalent ''L₁'' measure, Mean Integrated Absolute Error, is

: $\operatorname (\mathbf) = \operatorname\, \int , \hat_\mathbf (\mathbf) - f(\mathbf), \, d\mathbf.$

Its mathematical analysis is considerably more difficult than the MISE ones. In practice, the gain appears not to be significant. The ''L_∞'' norm is the Mean Uniform Absolute Error

: $\operatorname (\mathbf) = \operatorname\, \operatorname_ , \hat_\mathbf (\mathbf) - f(\mathbf), .$

which has been investigated only briefly. Likelihood error criteria include those based on the Mean Kullback–Leibler divergence

: \operatorname (\mathbf) = \int f(\mathbf) \, \operatorname (\mathbf)\, d\mathbf - \operatorname \int f(\mathbf) \, \operatorname hat(\mathbf;\mathbf)\, d\mathbf

and the Mean Hellinger distance

: $\operatorname (\mathbf) = \operatorname \int (\hat_\mathbf (\mathbf)^ - f(\mathbf)^)^2 \, d\mathbf .$

The KL can be estimated using a cross-validation method, although KL cross-validation selectors can be sub-optimal even if it remains consistent for bounded density functions. MH selectors have been briefly examined in the literature.

All these optimality criteria are distance based measures, and do not always correspond to more intuitive notions of closeness, so more visual criteria have been developed in response to this concern.

Objective and data-driven kernel selection

Recent research has shown that the kernel and its bandwidth can both be optimally and objectively chosen from the input data itself without making any assumptions about the form of the distribution. The resulting kernel density estimate converges rapidly to the true probability distribution as samples are added: at a rate close to the $n^$ expected for parametric estimators. This kernel estimator works for univariate and multivariate samples alike. The optimal kernel is defined in Fourier space—as the optimal damping function $\hat(\vec)$ (the Fourier transform of the kernel $\hat(\vec)$ )-- in terms of the Fourier transform of the data $\hat(\vec)$, the ''empirical characteristic function'' (see Kernel density estimation):

\hat(\vec) \equiv \frac \left 1 + \sqrt I_(\vec) \right/math>

$\hat(x) = \frac \int \hat\varphi(\vec)\psi_h(\vec) e^d\vec$

where, ''N'' is the number of data points, ''d'' is the number of dimensions (variables), and $I_(\vec)$ is a filter that is equal to 1 for 'accepted frequencies' and 0 otherwise. There are various ways to define this filter function, and a simple one that works for univariate or multivariate samples is called the 'lowest contiguous hypervolume filter'; $I_(\vec)$ is chosen such that the only accepted frequencies are a contiguous subset of frequencies surrounding the origin for which $, \hat(\vec), ^2 \ge 4(N-1)N^$ (see for a discussion of this and other filter functions).

Note that direct calculation of the ''empirical characteristic function'' (ECF) is slow, since it essentially involves a direct Fourier transform of the data samples. However, it has been found that the ECF can be approximated accurately using a non-uniform fast Fourier transform (nuFFT) method, which increases the calculation speed by several orders of magnitude (depending on the dimensionality of the problem). The combination of this objective KDE method and the nuFFT-based ECF approximation has been referred to as
fastKDE
' in the literature.

See also

* Kernel density estimation – univariate kernel density estimation.
* Variable kernel density estimation – estimation of multivariate densities using the kernel with variable bandwidth

References

External links

mvstat.net
A collection of peer-reviewed articles of the mathematical details of multivariate kernel density estimation and their bandwidth selectors on an {{mono, mvstat.net web page.

kde2d.m
A Matlab function for bivariate kernel density estimation.

libagf
A C++ library for multivariate, variable bandwidth kernel density estimation.

akde.m
A Matlab m-file for multivariate, variable bandwidth kernel density estimation.

helit
an

in th
PyQt-Fit package
are Python libraries for multivariate kernel density estimation.

Estimation of densities
Nonparametric statistics
Computational statistics
Multivariate statistics
Articles with example MATLAB/Octave code