Ludwig Boltzmann on:
[Wikipedia]
[Google]
[Amazon]
Ludwig Eduard Boltzmann (; 20 February 1844 – 5 September 1906) was an
 In 1872, long before women were admitted to Austrian universities, he met Henriette von Aigentler, an aspiring teacher of mathematics and physics in Graz. She was refused permission to audit lectures unofficially. Boltzmann supported her decision to appeal, which was successful. On 17 July 1876 Ludwig Boltzmann married Henriette; they had three daughters: Henriette (1880), Ida (1884) and Else (1891); and a son, Arthur Ludwig (1881). Boltzmann went back to Graz to take up the chair of Experimental Physics. Among his students in Graz were
In 1872, long before women were admitted to Austrian universities, he met Henriette von Aigentler, an aspiring teacher of mathematics and physics in Graz. She was refused permission to audit lectures unofficially. Boltzmann supported her decision to appeal, which was successful. On 17 July 1876 Ludwig Boltzmann married Henriette; they had three daughters: Henriette (1880), Ida (1884) and Else (1891); and a son, Arthur Ludwig (1881). Boltzmann went back to Graz to take up the chair of Experimental Physics. Among his students in Graz were
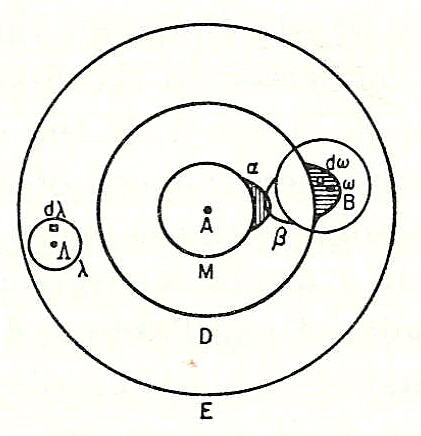
 The Boltzmann equation was developed to describe the dynamics of an ideal gas.
:
where ''ƒ'' represents the distribution function of single-particle position and momentum at a given time (see the
The Boltzmann equation was developed to describe the dynamics of an ideal gas.
:
where ''ƒ'' represents the distribution function of single-particle position and momentum at a given time (see the
 The idea that the
The idea that the
Chapter One: Girlhood in Vienna
gives Lise Meitner's account of Boltzmann's teaching and career. * Eftekhari, Ali,
Ludwig Boltzmann (1844–1906).
Discusses Boltzmann's philosophical opinions, with numerous quotes. * * * {{DEFAULTSORT:Boltzmann, Ludwig 1844 births 1906 suicides Scientists from Vienna 19th-century Austrian physicists Thermodynamicists Fluid dynamicists Burials at the Vienna Central Cemetery University of Vienna alumni Members of the Royal Swedish Academy of Sciences Corresponding members of the Saint Petersburg Academy of Sciences Suicides by hanging in Austria Foreign Members of the Royal Society Foreign associates of the National Academy of Sciences Mathematical physicists Theoretical physicists Rectors of universities in Austria 19th-century Austrian philosophers 20th-century Austrian philosophers Members of the Göttingen Academy of Sciences and Humanities
Austria
Austria, , bar, Östareich officially the Republic of Austria, is a country in the southern part of Central Europe, lying in the Eastern Alps. It is a federation of nine states, one of which is the capital, Vienna, the most populous ...
n physicist
A physicist is a scientist who specializes in the field of physics, which encompasses the interactions of matter and energy at all length and time scales in the physical universe.
Physicists generally are interested in the root or ultimate cau ...
and philosopher. His greatest achievements were the development of statistical mechanics, and the statistical explanation of the second law of thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unles ...
. In 1877 he provided the current definition of entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
, , where Ω is the number of microstates whose energy equals the system's energy, interpreted as a measure of statistical disorder of a system.
Max Planck
Max Karl Ernst Ludwig Planck (, ; 23 April 1858 – 4 October 1947) was a German theoretical physicist whose discovery of energy quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial contributions to theoretical p ...
named the constant the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
.
Statistical mechanics is one of the pillars of modern physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
. It describes how macroscopic
The macroscopic scale is the length scale on which objects or phenomena are large enough to be visible with the naked eye, without magnifying optical instruments. It is the opposite of microscopic.
Overview
When applied to physical phenomena a ...
observations (such as temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measurement, measured with a thermometer.
Thermometers are calibrated in various Conversion of units of temperature, temp ...
and pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and e ...
) are related to microscopic
The microscopic scale () is the scale of objects and events smaller than those that can easily be seen by the naked eye, requiring a lens or microscope to see them clearly. In physics, the microscopic scale is sometimes regarded as the scale be ...
parameters that fluctuate around an average. It connects thermodynamic quantities (such as heat capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K).
Heat capacity ...
) to microscopic behavior, whereas, in classical thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of ther ...
, the only available option would be to measure and tabulate such quantities for various materials.
Biography
Childhood and education
Boltzmann was born in Erdberg, a suburb ofVienna
en, Viennese
, iso_code = AT-9
, registration_plate = W
, postal_code_type = Postal code
, postal_code =
, timezone = CET
, utc_offset = +1
, timezone_DST ...
. His father, Ludwig Georg Boltzmann, was a revenue official. His grandfather, who had moved to Vienna from Berlin, was a clock manufacturer, and Boltzmann's mother, Katharina Pauernfeind, was originally from Salzburg
Salzburg (, ; literally "Salt-Castle"; bar, Soizbuag, label= Austro-Bavarian) is the fourth-largest city in Austria. In 2020, it had a population of 156,872.
The town is on the site of the Roman settlement of ''Iuvavum''. Salzburg was founded ...
. He received his primary education at the home of his parents. Boltzmann attended high school in Linz
Linz ( , ; cs, Linec) is the capital of Upper Austria and third-largest city in Austria. In the north of the country, it is on the Danube south of the Czech border. In 2018, the population was 204,846.
In 2009, it was a European Capital ...
, Upper Austria
Upper Austria (german: Oberösterreich ; bar, Obaöstareich) is one of the nine states or of Austria. Its capital is Linz. Upper Austria borders Germany and the Czech Republic, as well as the other Austrian states of Lower Austria, Styria, an ...
. When Boltzmann was 15, his father died.
Starting in 1863, Boltzmann studied mathematics and physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
at the University of Vienna
The University of Vienna (german: Universität Wien) is a public research university located in Vienna, Austria. It was founded by Duke Rudolph IV in 1365 and is the oldest university in the German-speaking world. With its long and rich hist ...
. He received his doctorate in 1866 and his venia legendi
Habilitation is the highest university degree, or the procedure by which it is achieved, in many European countries. The candidate fulfills a university's set criteria of excellence in research, teaching and further education, usually including a ...
in 1869. Boltzmann worked closely with Josef Stefan
Josef Stefan ( sl, Jožef Štefan; 24 March 1835 – 7 January 1893) was an ethnic Carinthian Slovene physicist, mathematician, and poet of the Austrian Empire.
Life and work
Stefan was born in an outskirt village of St. Peter (Slovene: ; to ...
, director of the institute of physics. It was Stefan who introduced Boltzmann to Maxwell's
Maxwell's, last known as Maxwell's Tavern, was a bar/restaurant and music club in Hoboken, New Jersey. Over several decades the venue attracted a wide variety of acts looking for a change from the New York City concert spaces across the river. Ma ...
work.
Academic career
In 1869 at age 25, thanks to a letter of recommendation written by Josef Stefan, Boltzmann was appointed full Professor ofMathematical Physics
Mathematical physics refers to the development of mathematical methods for application to problems in physics. The '' Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and the developme ...
at the University of Graz
The University of Graz (german: link=no, Karl-Franzens-Universität Graz, ), located in Graz, Austria, is the largest and oldest university in Styria, as well as the second-largest and second-oldest university in Austria.
History
The univers ...
in the province of Styria. In 1869 he spent several months in Heidelberg
Heidelberg (; Palatine German language, Palatine German: ''Heidlberg'') is a city in the States of Germany, German state of Baden-Württemberg, situated on the river Neckar in south-west Germany. As of the 2016 census, its population was 159,914 ...
working with Robert Bunsen
Robert Wilhelm Eberhard Bunsen (;
30 March 1811
– 16 August 1899) was a German chemist. He investigated emission spectra of heated elements, and discovered caesium (in 1860) and rubidium (in 1861) with the physicist Gustav Kirchhoff. The Bu ...
and Leo Königsberger and in 1871 with Gustav Kirchhoff
Gustav Robert Kirchhoff (; 12 March 1824 – 17 October 1887) was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects.
He ...
and Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz (31 August 1821 – 8 September 1894) was a German physicist and physician who made significant contributions in several scientific fields, particularly hydrodynamic stability. The Helmholtz Associatio ...
in Berlin. In 1873 Boltzmann joined the University of Vienna as Professor of Mathematics and there he stayed until 1876.
 In 1872, long before women were admitted to Austrian universities, he met Henriette von Aigentler, an aspiring teacher of mathematics and physics in Graz. She was refused permission to audit lectures unofficially. Boltzmann supported her decision to appeal, which was successful. On 17 July 1876 Ludwig Boltzmann married Henriette; they had three daughters: Henriette (1880), Ida (1884) and Else (1891); and a son, Arthur Ludwig (1881). Boltzmann went back to Graz to take up the chair of Experimental Physics. Among his students in Graz were
In 1872, long before women were admitted to Austrian universities, he met Henriette von Aigentler, an aspiring teacher of mathematics and physics in Graz. She was refused permission to audit lectures unofficially. Boltzmann supported her decision to appeal, which was successful. On 17 July 1876 Ludwig Boltzmann married Henriette; they had three daughters: Henriette (1880), Ida (1884) and Else (1891); and a son, Arthur Ludwig (1881). Boltzmann went back to Graz to take up the chair of Experimental Physics. Among his students in Graz were Svante Arrhenius
Svante August Arrhenius ( , ; 19 February 1859 – 2 October 1927) was a Swedish scientist. Originally a physicist, but often referred to as a chemist, Arrhenius was one of the founders of the science of physical chemistry. He received the Nob ...
and Walther Nernst. He spent 14 happy years in Graz and it was there that he developed his statistical concept of nature.
Boltzmann was appointed to the Chair of Theoretical Physics at the University of Munich
The Ludwig Maximilian University of Munich (simply University of Munich or LMU; german: Ludwig-Maximilians-Universität München) is a public research university in Munich, Germany. It is Germany's sixth-oldest university in continuous operatio ...
in Bavaria
Bavaria ( ; ), officially the Free State of Bavaria (german: Freistaat Bayern, link=no ), is a state in the south-east of Germany. With an area of , Bavaria is the largest German state by land area, comprising roughly a fifth of the total lan ...
, Germany in 1890.
In 1894, Boltzmann succeeded his teacher Joseph Stefan
Josef Stefan ( sl, Jožef Štefan; 24 March 1835 – 7 January 1893) was an ethnic Carinthian Slovene physicist, mathematician, and poet of the Austrian Empire.
Life and work
Stefan was born in an outskirt village of St. Peter (Slovene: ; to ...
as Professor of Theoretical Physics at the University of Vienna.
Final years and death
Boltzmann spent a great deal of effort in his final years defending his theories.Cercignani, Carlo (1998) Ludwig Boltzmann: The Man Who Trusted Atoms. Oxford University Press. He did not get along with some of his colleagues in Vienna, particularly Ernst Mach, who became a professor of philosophy and history of sciences in 1895. That same yearGeorg Helm
Georg Ferdinand Helm (; 15 March 1851 in Dresden, Saxony – 13 September 1923 in Dresden) was a German mathematician.
Helm graduated from high school from the Annenschule in Dresden in 1867. Thereafter he studied mathematics and natural sci ...
and Wilhelm Ostwald
Friedrich Wilhelm Ostwald (; 4 April 1932) was a Baltic German chemist and philosopher. Ostwald is credited with being one of the founders of the field of physical chemistry, with Jacobus Henricus van 't Hoff, Walther Nernst, and Svante Arrhen ...
presented their position on energetics at a meeting in Lübeck
Lübeck (; Low German also ), officially the Hanseatic City of Lübeck (german: Hansestadt Lübeck), is a city in Northern Germany. With around 217,000 inhabitants, Lübeck is the second-largest city on the German Baltic coast and in the state ...
. They saw energy, and not matter, as the chief component of the universe. Boltzmann's position carried the day among other physicists who supported his atomic theories in the debate. In 1900, Boltzmann went to the University of Leipzig
Leipzig University (german: Universität Leipzig), in Leipzig in Saxony, Germany, is one of the world's oldest universities and the second-oldest university (by consecutive years of existence) in Germany. The university was founded on 2 Decemb ...
, on the invitation of Wilhelm Ostwald
Friedrich Wilhelm Ostwald (; 4 April 1932) was a Baltic German chemist and philosopher. Ostwald is credited with being one of the founders of the field of physical chemistry, with Jacobus Henricus van 't Hoff, Walther Nernst, and Svante Arrhen ...
. Ostwald offered Boltzmann the professorial chair in physics, which became vacant when Gustav Heinrich Wiedemann died. After Mach retired due to bad health, Boltzmann returned to Vienna in 1902. In 1903, Boltzmann, together with Gustav von Escherich and Emil Müller, founded the Austrian Mathematical Society
The Austrian Mathematical Society (german: Österreichische Mathematische Gesellschaft) is the national mathematical society of Austria and a member society of the European Mathematical Society.
History
The society was founded in 1903 by Ludwig B ...
. His students included Karl Přibram, Paul Ehrenfest
Paul Ehrenfest (18 January 1880 – 25 September 1933) was an Austrian theoretical physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition a ...
and Lise Meitner.
In Vienna, Boltzmann taught physics and also lectured on philosophy. Boltzmann's lectures on natural philosophy
Natural philosophy or philosophy of nature (from Latin ''philosophia naturalis'') is the philosophical study of physics, that is, nature and the physical universe. It was dominant before the development of modern science.
From the ancient wo ...
were very popular and received considerable attention. His first lecture was an enormous success. Even though the largest lecture hall had been chosen for it, the people stood all the way down the staircase. Because of the great successes of Boltzmann's philosophical lectures, the Emperor invited him for a reception at the Palace.
In 1906, Boltzmann's deteriorating mental condition forced him to resign his position, and his symptoms indicate he experienced what would today be diagnosed as bipolar disorder
Bipolar disorder, previously known as manic depression, is a mental disorder characterized by periods of depression and periods of abnormally elevated mood that last from days to weeks each. If the elevated mood is severe or associated with ...
. Four months later he died by suicide on 5 September 1906, by hanging
Hanging is the suspension of a person by a noose or ligature around the neck.Oxford English Dictionary, 2nd ed. Hanging as method of execution is unknown, as method of suicide from 1325. The ''Oxford English Dictionary'' states that hanging ...
himself while on vacation with his wife and daughter in Duino
Duino ( sl, Devin, german: Tybein) is today a seaside resort on the northern Adriatic coast. It is a ''hamlet'' of Duino-Aurisina, a municipality (''comune'') of the Friuli–Venezia Giulia region of northeastern Italy. The settlement, picturesq ...
, near Trieste
Trieste ( , ; sl, Trst ; german: Triest ) is a city and seaport in northeastern Italy. It is the capital city, and largest city, of the autonomous region of Friuli Venezia Giulia, one of two autonomous regions which are not subdivided into prov ...
(then Austria).
He is buried in the Viennese Zentralfriedhof
The Vienna Central Cemetery (german: Wiener Zentralfriedhof) is one of the largest cemeteries in the world by number of interred, and is the most well-known cemetery among Vienna's nearly 50 cemeteries. The cemetery's name is descriptive of its ...
. His tombstone bears the inscription of Boltzmann's entropy formula
In statistical mechanics, Boltzmann's equation (also known as the Boltzmann–Planck equation) is a probability equation relating the entropy S, also written as S_\mathrm, of an ideal gas to the multiplicity (commonly denoted as \Omega or W), the ...
: .
Philosophy
Boltzmann's kinetic theory of gases seemed to presuppose the reality ofatom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas, ...
s and molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
s, but almost all German philosophers and many scientists like Ernst Mach and the physical chemist
Physical chemistry is the study of macroscopic and microscopic phenomena in chemical systems in terms of the principles, practices, and concepts of physics such as motion, energy, force, time, thermodynamics, quantum chemistry, statistical mech ...
Wilhelm Ostwald
Friedrich Wilhelm Ostwald (; 4 April 1932) was a Baltic German chemist and philosopher. Ostwald is credited with being one of the founders of the field of physical chemistry, with Jacobus Henricus van 't Hoff, Walther Nernst, and Svante Arrhen ...
disbelieved their existence.
Physics
Boltzmann's most important scientific contributions were in kinetic theory, including for motivating theMaxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and use ...
as a description of molecular speeds in a gas. Maxwell–Boltzmann statistics
In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...
and the Boltzmann distribution
In statistical mechanics and mathematics, a Boltzmann distribution (also called Gibbs distribution Translated by J.B. Sykes and M.J. Kearsley. See section 28) is a probability distribution or probability measure that gives the probability th ...
remain central in the foundations of classical statistical mechanics. They are also applicable to other phenomena that do not require quantum statistics and provide insight into the meaning of temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measurement, measured with a thermometer.
Thermometers are calibrated in various Conversion of units of temperature, temp ...
.

Most
Most or Möst or ''variation'', may refer to:
Places
* Most, Kardzhali Province, a village in Bulgaria
* Most (city), a city in the Czech Republic
** Most District, a district surrounding the city
** Most Basin, a lowland named after the city
** A ...
chemist
A chemist (from Greek ''chēm(ía)'' alchemy; replacing ''chymist'' from Medieval Latin ''alchemist'') is a scientist trained in the study of chemistry. Chemists study the composition of matter and its properties. Chemists carefully describe t ...
s, since the discoveries of John Dalton in 1808, and James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish mathematician and scientist responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and li ...
in Scotland and Josiah Willard Gibbs
Josiah Willard Gibbs (; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in t ...
in the United States, shared Boltzmann's belief in atom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas, ...
s and molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
s, but much of the physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
establishment did not share this belief until decades later. Boltzmann had a long-running dispute with the editor of the preeminent German physics journal of his day, who refused to let Boltzmann refer to atoms and molecules as anything other than convenient theoretical
A theory is a rational type of abstract thinking about a phenomenon, or the results of such thinking. The process of contemplative and rational thinking is often associated with such processes as observational study or research. Theories may be ...
constructs. Only a couple of years after Boltzmann's death, Perrin's studies of colloidal suspensions (1908–1909), based on Einstein's theoretical studies of 1905, confirmed the values of the Avogadro constant
The Avogadro constant, commonly denoted or , is the proportionality factor that relates the number of constituent particles (usually molecules, atoms or ions) in a sample with the amount of substance in that sample. It is an SI defining c ...
and the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
, convincing the world that the tiny particles really exist.
To quote Planck
Max Karl Ernst Ludwig Planck (, ; 23 April 1858 – 4 October 1947) was a German theoretical physicist whose discovery of energy quanta won him the Nobel Prize in Physics in 1918.
Planck made many substantial contributions to theoretical p ...
, "The logarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of ...
ic connection between entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
and probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speakin ...
was first stated by L. Boltzmann in his kinetic theory of gases". This famous formula for entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynam ...
''S'' is
:
where ''k''B is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
, and ln is the natural logarithm. ''W'' is ''Wahrscheinlichkeit'', a German word meaning the probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speakin ...
of occurrence of a macrostate or, more precisely, the number of possible microstates corresponding to the macroscopic state of a system — the number of (unobservable) "ways" in the (observable) thermodynamic
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of the ...
state of a system that can be realized by assigning different positions and momenta to the various molecules. Boltzmann's paradigm was an ideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is a ...
of ''N'' ''identical'' particles, of which ''N''''i'' are in the ''i''th microscopic condition (range) of position and momentum. ''W'' can be counted using the formula for permutations
:
where ''i'' ranges over all possible molecular conditions, and where denotes factorial. The "correction" in the denominator account for indistinguishable particles in the same condition.
Boltzmann could also be considered one of the forerunners of quantum mechanics due to his suggestion in 1877 that the energy levels of a physical system could be discrete.
Boltzmann equation
Maxwell–Boltzmann distribution
In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.
It was first defined and use ...
), ''F'' is a force, ''m'' is the mass of a particle, ''t'' is the time and ''v'' is an average velocity of particles.
This equation describes the temporal and spatial variation of the probability distribution for the position and momentum of a density distribution of a cloud of points in single-particle phase space. (See Hamiltonian mechanics
Hamiltonian mechanics emerged in 1833 as a reformulation of Lagrangian mechanics. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (generalized) ''momenta ...
.) The first term on the left-hand side represents the explicit time variation of the distribution function, while the second term gives the spatial variation, and the third term describes the effect of any force acting on the particles. The right-hand side of the equation represents the effect of collisions.
In principle, the above equation completely describes the dynamics of an ensemble of gas particles, given appropriate boundary conditions. This first-order differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
has a deceptively simple appearance, since ''f'' can represent an arbitrary single-particle distribution function. Also, the force acting on the particles depends directly on the velocity distribution function ''f''. The Boltzmann equation is notoriously difficult to integrate. David Hilbert spent years trying to solve it without any real success.
The form of the collision term assumed by Boltzmann was approximate. However, for an ideal gas the standard Chapman–Enskog solution of the Boltzmann equation is highly accurate. It is expected to lead to incorrect results for an ideal gas only under shock wave
In physics, a shock wave (also spelled shockwave), or shock, is a type of propagating disturbance that moves faster than the local speed of sound in the medium. Like an ordinary wave, a shock wave carries energy and can propagate through a me ...
conditions.
Boltzmann tried for many years to "prove" the second law of thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unles ...
using his gas-dynamical equation — his famous H-theorem
In classical statistical mechanics, the ''H''-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency to decrease in the quantity ''H'' (defined below) in a nearly-ideal gas of molecules.
L. Boltzmann,Weitere Studien über das Wä ...
. However the key assumption he made in formulating the collision term was "molecular chaos
In the kinetic theory of gases in physics, the molecular chaos hypothesis (also called ''Stosszahlansatz'' in the writings of Paul Ehrenfest) is the assumption that the velocities of colliding particles are uncorrelated, and independent of positi ...
", an assumption which breaks time-reversal symmetry
T-symmetry or time reversal symmetry is the theoretical symmetry of physical laws under the transformation of time reversal,
: T: t \mapsto -t.
Since the second law of thermodynamics states that entropy increases as time flows toward the futur ...
as is necessary for ''anything'' which could imply the second law. It was from the probabilistic assumption alone that Boltzmann's apparent success emanated, so his long dispute with Loschmidt and others over Loschmidt's paradox
Loschmidt's paradox, also known as the reversibility paradox, irreversibility paradox or ', is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of (al ...
ultimately ended in his failure.
Finally, in the 1970s E.G.D. Cohen and J. R. Dorfman proved that a systematic (power series) extension of the Boltzmann equation to high densities is mathematically impossible. Consequently, nonequilibrium statistical mechanics for dense gases and liquids focuses on the Green–Kubo relations
The Green–Kubo relations ( Melville S. Green 1954, Ryogo Kubo 1957) give the exact mathematical expression for transport coefficients \gamma in terms of integrals of time correlation functions:
:\gamma = \int_0^\infty \left\langle \dot(t) \dot ...
, the fluctuation theorem
The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium (i.e., maximum entropy) will increase or decrease ov ...
, and other approaches instead.
Second thermodynamics law as a law of disorder
second law of thermodynamics
The second law of thermodynamics is a physical law based on universal experience concerning heat and energy interconversions. One simple statement of the law is that heat always moves from hotter objects to colder objects (or "downhill"), unles ...
or "entropy law" is a law of disorder (or that dynamically ordered states are "infinitely improbable") is due to Boltzmann's view of the second law of thermodynamics.
In particular, it was Boltzmann's attempt to reduce it to a stochastic collision function, or law of probability following from the random collisions of mechanical particles. Following Maxwell, Boltzmann modeled gas molecules as colliding billiard balls in a box, noting that with each collision nonequilibrium velocity distributions (groups of molecules moving at the same speed and in the same direction) would become increasingly disordered leading to a final state of macroscopic uniformity and maximum microscopic disorder or the state of maximum entropy (where the macroscopic uniformity corresponds to the obliteration of all field potentials or gradients). The second law, he argued, was thus simply the result of the fact that in a world of mechanically colliding particles disordered states are the most probable. Because there are so many more possible disordered states than ordered ones, a system will almost always be found either in the state of maximum disorder – the macrostate with the greatest number of accessible microstates such as a gas in a box at equilibrium – or moving towards it. A dynamically ordered state, one with molecules moving "at the same speed and in the same direction", Boltzmann concluded, is thus "the most improbable case conceivable...an infinitely improbable configuration of energy."
Boltzmann accomplished the feat of showing that the second law of thermodynamics is only a statistical fact. The gradual disordering of energy is analogous to the disordering of an initially ordered pack of cards under repeated shuffling, and just as the cards will finally return to their original order if shuffled a gigantic number of times, so the entire universe must some-day regain, by pure chance, the state from which it first set out. (This optimistic coda to the idea of the dying universe becomes somewhat muted when one attempts to estimate the timeline which will probably elapse before it spontaneously occurs.) The tendency for entropy increase seems to cause difficulty to beginners in thermodynamics, but is easy to understand from the standpoint of the theory of probability. Consider two ordinary dice, with both sixes face up. After the dice are shaken, the chance of finding these two sixes face up is small (1 in 36); thus one can say that the random motion (the agitation) of the dice, like the chaotic collisions of molecules because of thermal energy, causes the less probable state to change to one that is more probable. With millions of dice, like the millions of atoms involved in thermodynamic calculations, the probability of their all being sixes becomes so vanishingly small that the system ''must'' move to one of the more probable states."Collier's Encyclopedia", Volume 22 Sylt to Uruguay, Thermodynamics, by Leo Peters, p. 275
Works
* * * * *Awards and honours
In 1885 he became a member of the Imperial Austrian Academy of Sciences and in 1887 he became the President of theUniversity of Graz
The University of Graz (german: link=no, Karl-Franzens-Universität Graz, ), located in Graz, Austria, is the largest and oldest university in Styria, as well as the second-largest and second-oldest university in Austria.
History
The univers ...
. He was elected a member of the Royal Swedish Academy of Sciences in 1888 and a Foreign Member of the Royal Society (ForMemRS) in 1899. Numerous things are named in his honour.
See also
*Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of th ...
* Boltzmann brain
The Boltzmann brain thought experiment suggests that it might be more likely for a single brain to spontaneously form in a void (complete with a memory of having existed in our universe) rather than for the entire universe to come about in the m ...
References
Further reading
* Roman Sexl & John Blackmore (eds.), "Ludwig Boltzmann – Ausgewahlte Abhandlungen", (Ludwig Boltzmann Gesamtausgabe, Band 8), Vieweg, Braunschweig, 1982. * John Blackmore (ed.), "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book One: A Documentary History", Kluwer, 1995. * John Blackmore, "Ludwig Boltzmann – His Later Life and Philosophy, 1900–1906, Book Two: The Philosopher", Kluwer, Dordrecht, Netherlands, 1995. * John Blackmore (ed.), "Ludwig Boltzmann – Troubled Genius as Philosopher", in Synthese, Volume 119, Nos. 1 & 2, 1999, pp. 1–232. * * Boltzmann, ''Ludwig Boltzmann – Leben und Briefe'', ed., Walter Hoeflechner, Akademische Druck- u. Verlagsanstalt. Graz, Oesterreich, 1994 * Brush, Stephen G. (ed. & tr.), Boltzmann, ''Lectures on Gas Theory'', Berkeley, California: U. of California Press, 1964 * Brush, Stephen G. (ed.), ''Kinetic Theory'', New York: Pergamon Press, 1965 * * * * * Ehrenfest, P. & Ehrenfest, T. (1911) "Begriffliche Grundlagen der statistischen Auffassung in der Mechanik", in ''Encyklopädie der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen'' Band IV, 2. Teil ( F. Klein and C. Müller (eds.). Leipzig: Teubner, pp. 3–90. Translated as ''The Conceptual Foundations of the Statistical Approach in Mechanics''. New York: Cornell University Press, 1959. * * * * * * * * * English translation by Morton Masius of the 2nd ed. of ''Waermestrahlung''. Reprinted by Dover (1959) & (1991). * Sharp, Kim (2019). ''Entropy and the Tao of Counting: A Brief Introduction to Statistical Mechanics and the Second Law of Thermodynamics'' (SpringerBriefs in Physics). Springer Nature. * Reprinted: Dover (1979).External links
* * * Ruth Lewin Sime, ''Lise Meitner: A Life in Physics'Chapter One: Girlhood in Vienna
gives Lise Meitner's account of Boltzmann's teaching and career. * Eftekhari, Ali,
Ludwig Boltzmann (1844–1906).
Discusses Boltzmann's philosophical opinions, with numerous quotes. * * * {{DEFAULTSORT:Boltzmann, Ludwig 1844 births 1906 suicides Scientists from Vienna 19th-century Austrian physicists Thermodynamicists Fluid dynamicists Burials at the Vienna Central Cemetery University of Vienna alumni Members of the Royal Swedish Academy of Sciences Corresponding members of the Saint Petersburg Academy of Sciences Suicides by hanging in Austria Foreign Members of the Royal Society Foreign associates of the National Academy of Sciences Mathematical physicists Theoretical physicists Rectors of universities in Austria 19th-century Austrian philosophers 20th-century Austrian philosophers Members of the Göttingen Academy of Sciences and Humanities