Lambert cylindrical equal-area projection on:
[Wikipedia]
[Google]
[Amazon]
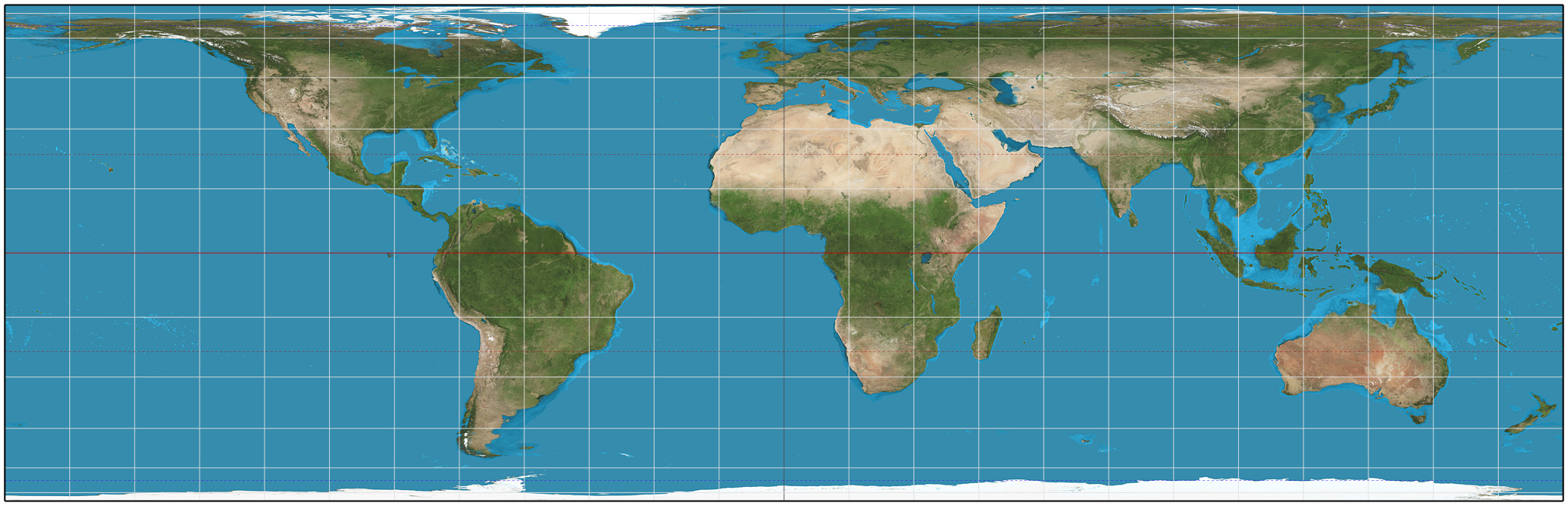

 In
In
 The projection was invented by the
The projection was invented by the
Table of examples and properties of all common projections
from radicalcartography.net {{DEFAULTSORT:Lambert Cylindrical Equal-Area Projection Cylindrical equal-area projections

cartography
Cartography (; from , 'papyrus, sheet of paper, map'; and , 'write') is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can ...
, the Lambert cylindrical equal-area projection, or Lambert cylindrical projection, is a
cylindrical equal-area projection
In cartography, the normal cylindrical equal-area projection is a family of Map projection#Normal cylindrical, normal cylindrical, equal-area projection, equal-area map projections.
History
The invention of the Lambert cylindrical equal-area pr ...
. This projection is undistorted along the equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
, which is its standard parallel, but distortion increases rapidly towards the poles. Like any cylindrical projection, it stretches parallels increasingly away from the equator. The poles accrue infinite distortion, becoming lines instead of points.
History
 The projection was invented by the
The projection was invented by the Swiss
Swiss most commonly refers to:
* the adjectival form of Switzerland
* Swiss people
Swiss may also refer to: Places
* Swiss, Missouri
* Swiss, North Carolina
* Swiss, West Virginia
* Swiss, Wisconsin
Other uses
* Swiss Café, an old café located ...
mathematician Johann Heinrich Lambert
Johann Heinrich Lambert (; ; 26 or 28 August 1728 – 25 September 1777) was a polymath from the Republic of Mulhouse, at that time allied to the Switzerland, Swiss Confederacy, who made important contributions to the subjects of mathematics, phys ...
and described in his 1772 treatise, ''Beiträge zum Gebrauche der Mathematik und deren Anwendung'', part III, section 6: ''Anmerkungen und Zusätze zur Entwerfung der Land- und Himmelscharten'', translated as, ''Notes and Comments on the Composition of Terrestrial and Celestial Maps''.
Lambert's projection is the basis for the cylindrical equal-area projection family. Lambert chose the equator as the parallel of no distortion. By multiplying the projection's height by some factor and dividing the width by the same factor, the regions of no distortion can be moved to any desired pair of parallels north and south of the equator. These variations, particularly the Gall–Peters projection
The Gall–Peters projection is a rectangular, Equal-area projection, equal-area map projection. Like all equal-area projections, it distorts most shapes. It is a cylindrical equal-area projection with latitudes 45° north and south as the regions ...
, are more commonly encountered in maps than Lambert’s original projection due to their lower distortion overall.
Formulae
: where is thelatitude
In geography, latitude is a geographic coordinate system, geographic coordinate that specifies the north-south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at t ...
, is the longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
and is the central meridian.
See also
*List of map projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections,
there can be no comprehensive list.
Table of proj ...
*Lambert azimuthal equal-area projection
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann ...
* Lambert conformal conic projection
References
External links
*Table of examples and properties of all common projections
from radicalcartography.net {{DEFAULTSORT:Lambert Cylindrical Equal-Area Projection Cylindrical equal-area projections