Frictional contact mechanics on:
[Wikipedia]
[Google]
[Amazon]
Contact mechanics
Contact mechanics is the study of the deformation of solids that touch each other at one or more points.Johnson, K. L, 1985, Contact mechanics, Cambridge University Press.Popov, Valentin L., 2010, ''Contact Mechanics and Friction. Physical P ...
is the study of the deformation of solids
Solid is one of the four fundamental states of matter (the others being liquid, gas, and plasma). The molecules in a solid are closely packed together and contain the least amount of kinetic energy. A solid is characterized by structural ...
that touch each other at one or more points. This can be divided into compressive and adhesive forces in the direction perpendicular to the interface, and friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of ...
al forces in the tangential direction. Frictional contact mechanics is the study of the deformation of bodies in the presence of frictional effects, whereas '' frictionless contact mechanics'' assumes the absence of such effects.
Frictional contact mechanics is concerned with a large range of different scales.
* At the macroscopic scale, it is applied for the investigation of the motion of contacting bodies (see Contact dynamics
Contact dynamics deals with the motion of multibody systems subjected to unilateral contacts and friction. Such systems are omnipresent in many multibody dynamics applications. Consider for example
* Contacts between wheels and ground in vehicle ...
). For instance the bouncing of a rubber ball on a surface depends on the frictional interaction at the contact interface. Here the total force versus indentation and lateral displacement are of main concern.
* At the intermediate scale, one is interested in the local stresses, strains and deformations of the contacting bodies in and near the contact area. For instance to derive or validate contact models at the macroscopic scale, or to investigate wear
Wear is the damaging, gradual removal or deformation of material at solid surfaces. Causes of wear can be mechanical (e.g., erosion) or chemical (e.g., corrosion). The study of wear and related processes is referred to as tribology.
Wear in ...
and damage
Damage is any change in a thing, often a physical object, that degrades it away from its initial state. It can broadly be defined as "changes introduced into a system that adversely affect its current or future performance".Farrar, C.R., Sohn, H., ...
of the contacting bodies' surfaces. Application areas of this scale are tire-pavement interaction, railway wheel-rail interaction, roller bearing analysis, etc.
* Finally, at the microscopic and nano-scales, contact mechanics is used to increase our understanding of tribological systems (e.g., investigate the origin of friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of ...
) and for the engineering of advanced devices like atomic force microscope
Atomic force microscopy (AFM) or scanning force microscopy (SFM) is a very-high-resolution type of scanning probe microscopy (SPM), with demonstrated resolution on the order of fractions of a nanometer, more than 1000 times better than the op ...
s and MEMS
Microelectromechanical systems (MEMS), also written as micro-electro-mechanical systems (or microelectronic and microelectromechanical systems) and the related micromechatronics and microsystems constitute the technology of microscopic devices, ...
devices.
This page is mainly concerned with the second scale: getting basic insight in the stresses and deformations in and near the contact patch, without paying too much attention to the detailed mechanisms by which they come about.
History
Several famous scientists, engineers and mathematicians contributed to our understanding of friction. They includeLeonardo da Vinci
Leonardo di ser Piero da Vinci (15 April 14522 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor, and architect. While his fame initially rested on ...
, Guillaume Amontons
Guillaume Amontons (31 August 1663 – 11 October 1705) was a French scientific instrument inventor and physicist. He was one of the pioneers in studying the problem of friction, which is the resistance to motion when bodies make contact. He is ...
, John Theophilus Desaguliers
John Theophilus Desaguliers FRS (12 March 1683 – 29 February 1744) was a British natural philosopher, clergyman, engineer and freemason who was elected to the Royal Society in 1714 as experimental assistant to Isaac Newton. He had studied at ...
, Leonhard Euler
Leonhard Euler ( , ; 15 April 170718 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries ...
, and Charles-Augustin de Coulomb
Charles-Augustin de Coulomb (; ; 14 June 1736 – 23 August 1806) was a French officer, engineer, and physicist. He is best known as the eponymous discoverer of what is now called Coulomb's law, the description of the electrostatic force of attra ...
. Later, Nikolai Pavlovich Petrov, Osborne Reynolds
Osborne Reynolds (23 August 1842 – 21 February 1912) was an Irish-born innovator in the understanding of fluid dynamics. Separately, his studies of heat transfer between solids and fluids brought improvements in boiler and condenser design. ...
and Richard Stribeck Richard Stribeck (7. July 1861 in Stuttgart , † 29. March 1950) was a German engineer, after whom the Stribeck Curve is named.
Life
Stribeck studied mechanical engineering in 1880 at the Technical University of Stuttgart in 1885 and worked as a ...
supplemented this understanding with theories of lubrication
Lubrication is the process or technique of using a lubricant to reduce friction and wear and tear in a contact between two surfaces. The study of lubrication is a discipline in the field of tribology.
Lubrication mechanisms such as fluid-lubric ...
.
Deformation of solid materials was investigated in the 17th and 18th centuries by Robert Hooke
Robert Hooke FRS (; 18 July 16353 March 1703) was an English polymath active as a scientist, natural philosopher and architect, who is credited to be one of two scientists to discover microorganisms in 1665 using a compound microscope that ...
, Joseph Louis Lagrange
Joseph-Louis Lagrange (born Giuseppe Luigi Lagrangiad’Alembert and Timoshenko. With respect to contact mechanics the classical contribution by 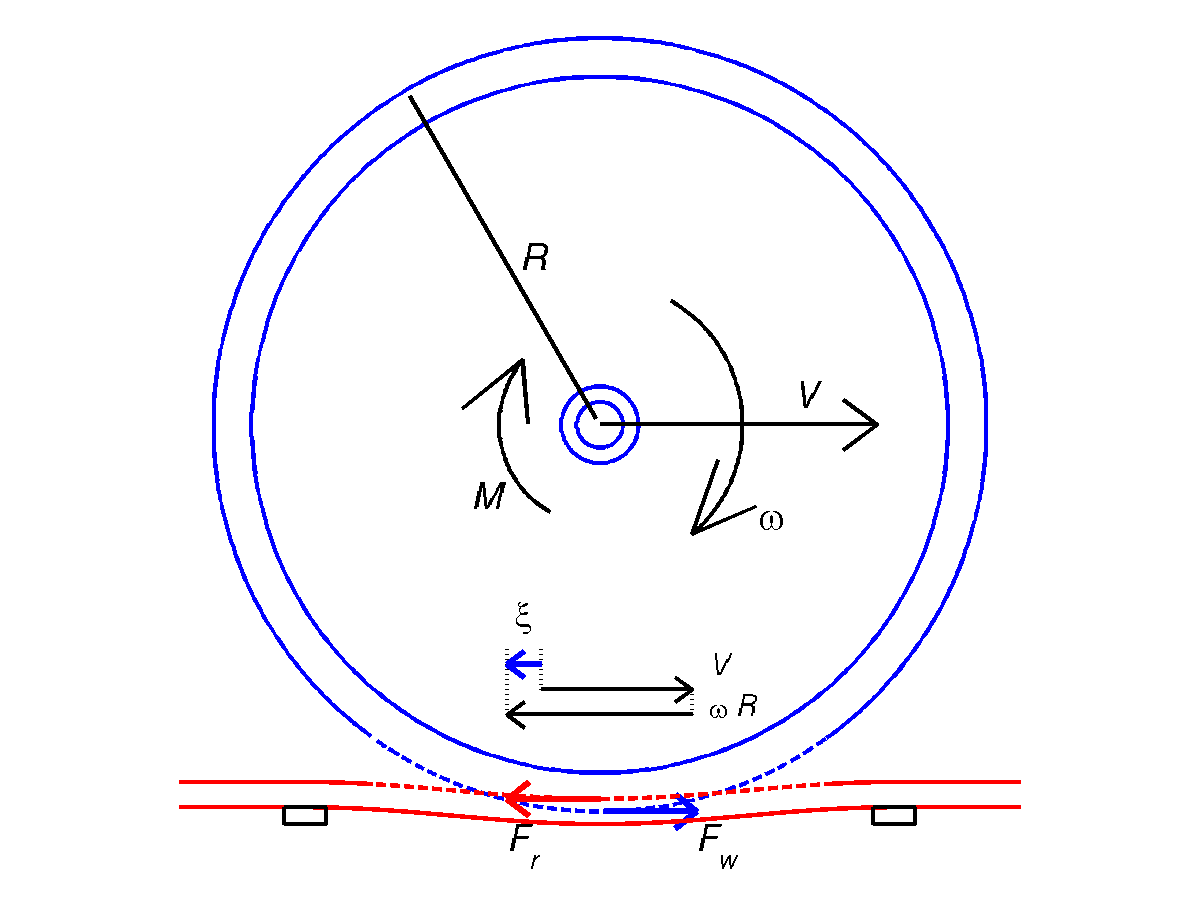 Classical results for a true frictional contact problem concern the papers by F.W. Carter (1926) and H. Fromm (1927). They independently presented the creep versus creep force relation for a cylinder on a plane or for two cylinders in steady rolling contact using Coulomb’s dry friction law (see below). These are applied to railway locomotive traction, and for understanding the
Classical results for a true frictional contact problem concern the papers by F.W. Carter (1926) and H. Fromm (1927). They independently presented the creep versus creep force relation for a cylinder on a plane or for two cylinders in steady rolling contact using Coulomb’s dry friction law (see below). These are applied to railway locomotive traction, and for understanding the
Heinrich Hertz
Heinrich Rudolf Hertz ( ; ; 22 February 1857 – 1 January 1894) was a German physicist who first conclusively proved the existence of the electromagnetic waves predicted by James Clerk Maxwell's equations of electromagnetism. The uni ...
stands out. Further the fundamental solutions by Boussinesq and Cerruti are of primary importance for the investigation of frictional contact problems in the (linearly) elastic regime.
 Classical results for a true frictional contact problem concern the papers by F.W. Carter (1926) and H. Fromm (1927). They independently presented the creep versus creep force relation for a cylinder on a plane or for two cylinders in steady rolling contact using Coulomb’s dry friction law (see below). These are applied to railway locomotive traction, and for understanding the
Classical results for a true frictional contact problem concern the papers by F.W. Carter (1926) and H. Fromm (1927). They independently presented the creep versus creep force relation for a cylinder on a plane or for two cylinders in steady rolling contact using Coulomb’s dry friction law (see below). These are applied to railway locomotive traction, and for understanding the hunting oscillation
Hunting oscillation is a self-oscillation, usually unwanted, about an equilibrium. The expression came into use in the 19th century and describes how a system "hunts" for equilibrium. The expression is used to describe phenomena in such diverse ...
of railway vehicles. With respect to sliding, the classical solutions are due to C. Cattaneo (1938) and R.D. Mindlin (1949), who considered the tangential shifting of a sphere on a plane (see below).
In the 1950s, interest in the rolling contact of railway wheels grew. In 1958, Kenneth L. Johnson presented an approximate approach for the 3D frictional problem with Hertzian geometry, with either lateral or spin creepage. Among others he found that spin creepage, which is symmetric about the center of the contact patch, leads to a net lateral force in rolling conditions. This is due to the fore-aft differences in the distribution of tractions in the contact patch.
In 1967, Joost Jacques Kalker published his milestone PhD thesis on the linear theory for rolling contact. This theory is exact for the situation of an infinite friction coefficient in which case the slip area vanishes, and is approximative for non-vanishing creepages. It does assume Coulomb's friction law, which more or less requires (scrupulously) clean surfaces. This theory is for massive bodies such as the railway wheel-rail contact. With respect to road-tire interaction, an important contribution concerns the so-called magic tire formula by Hans Pacejka Hans Bastiaan Pacejka (12 September 1934 – 17 September 2017) was an expert in vehicle system dynamics and particularly in tire dynamics, fields in which his works are now standard references. He was Professor emeritus at Delft University of Tec ...
.
In the 1970s, many numerical models were devised. Particularly variational approaches, such as those relying on Duvaut and Lion’s existence and uniqueness theories. Over time, these grew into finite element approaches for contact problems with general material models and geometries, and into half-space based approaches for so-called smooth-edged contact problems for linearly elastic materials. Models of the first category were presented by LaursenLaursen, T.A., 2002, ''Computational Contact and Impact Mechanics, Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis'', Springer, Berlin and by Wriggers.Wriggers, P., 2006, ''Computational Contact Mechanics, 2nd ed.'', Springer, Heidelberg An example of the latter category is Kalker’s CONTACT model.
A drawback of the well-founded variational approaches is their large computation times. Therefore, many different approximate approaches were devised as well. Several well-known approximate theories for the rolling contact problem are Kalker’s FASTSIM approach, the Shen-Hedrick-Elkins formula, and Polach’s approach.
More information on the history of the wheel/rail contact problem is provided in Knothe's paper. Further Johnson collected in his book a tremendous amount of information on contact mechanics and related subjects. With respect to rolling contact mechanics an overview of various theories is presented by Kalker as well. Finally the proceedings of a CISM course are of interest, which provide an introduction to more advanced aspects of rolling contact theory.
Problem formulation
Central in the analysis of frictional contact problems is the understanding that the stresses at the surface of each body are spatially varying. Consequently, the strains and deformations of the bodies are varying with position too. And the motion of particles of the contacting bodies can be different at different locations: in part of the contact patch particles of the opposing bodies may adhere (stick) to each other, whereas in other parts of the contact patch relative movement occurs. This local relative sliding is called micro- slip. This subdivision of the contact area into stick (adhesion) and slip areas manifests itself a.o. in fretting wear. Note thatwear
Wear is the damaging, gradual removal or deformation of material at solid surfaces. Causes of wear can be mechanical (e.g., erosion) or chemical (e.g., corrosion). The study of wear and related processes is referred to as tribology.
Wear in ...
occurs only where power
Power most often refers to:
* Power (physics), meaning "rate of doing work"
** Engine power, the power put out by an engine
** Electric power
* Power (social and political), the ability to influence people or events
** Abusive power
Power may a ...
is dissipated, which requires stress and local relative displacement (slip) between the two surfaces.
The size and shape of the contact patch itself and of its adhesion and slip areas are generally unknown in advance. If these were known, then the elastic fields in the two bodies could be solved independently from each other and the problem would not be a contact problem anymore.
Three different components can be distinguished in a contact problem.
# First of all, there is the deformation of the separate bodies in reaction to loads applied on their surfaces. This is the subject of general continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such mo ...
. It depends largely on the geometry of the bodies and on their ( constitutive) material behavior (e.g. elastic
Elastic is a word often used to describe or identify certain types of elastomer, elastic used in garments or stretchable fabrics.
Elastic may also refer to:
Alternative name
* Rubber band, ring-shaped band of rubber used to hold objects togethe ...
vs. plastic
Plastics are a wide range of synthetic or semi-synthetic materials that use polymers as a main ingredient. Their plasticity makes it possible for plastics to be moulded, extruded or pressed into solid objects of various shapes. This adapta ...
response, homogeneous vs. layered structure etc.).
# Secondly, there is the overall motion of the bodies relative to each other. For instance the bodies can be at rest (statics) or approaching each other quickly (impact
Impact may refer to:
* Impact (mechanics), a high force or shock (mechanics) over a short time period
* Impact, Texas, a town in Taylor County, Texas, US
Science and technology
* Impact crater, a meteor crater caused by an impact event
* Imp ...
), and can be shifted (sliding) or rotated (rolling
Rolling is a type of motion that combines rotation (commonly, of an axially symmetric object) and translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact ...
) over each other. These overall motions are generally studied in classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classi ...
, see for instance multibody dynamics.
# Finally there are the processes at the contact interface: compression and adhesion
Adhesion is the tendency of dissimilar particles or surfaces to cling to one another ( cohesion refers to the tendency of similar or identical particles/surfaces to cling to one another).
The forces that cause adhesion and cohesion can ...
in the direction perpendicular to the interface, and friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of ...
and micro-slip in the tangential directions.
The last aspect is the primary concern of contact mechanics. It is described in terms of so-called ''contact conditions''.
For the direction perpendicular to the interface, the normal contact problem, adhesion effects are usually small (at larger spatial scales) and the following conditions are typically employed:
# The gap between the two surfaces must be zero (contact) or strictly positive (separation, );
# The normal stress acting on each body is zero (separation) or compressive ( in contact).
Mathematically: . Here are functions that vary with the position along the bodies' surfaces.
In the tangential directions the following conditions are often used:
# The local (tangential) shear stress (assuming the normal direction parallel to the -axis) cannot exceed a certain position-dependent maximum, the so-called traction bound ;
# Where the magnitude of tangential traction falls below the traction bound