Equals sign on:
[Wikipedia]
[Google]
[Amazon]
The equals sign (
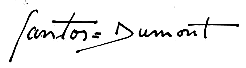 A possibly unique case of the equals sign of European usage in a person's name, specifically in a double-barreled name, was by the aviation pioneer Alberto Santos-Dumont, as he is also known not only to have often used a double hyphen resembling an equal sign between his two surnames in place of a hyphen, but also seems to have personally preferred that practice, to display equal respect for his father's French ethnicity and the Brazilian ethnicity of his mother.
Instead of a double hyphen, the equals sign is sometimes used in Japanese as a separator between names. In
A possibly unique case of the equals sign of European usage in a person's name, specifically in a double-barreled name, was by the aviation pioneer Alberto Santos-Dumont, as he is also known not only to have often used a double hyphen resembling an equal sign between his two surnames in place of a hyphen, but also seems to have personally preferred that practice, to display equal respect for his father's French ethnicity and the Brazilian ethnicity of his mother.
Instead of a double hyphen, the equals sign is sometimes used in Japanese as a separator between names. In
Earliest Uses of Symbols of RelationImage of the page of ''The Whetstone of Witte'' on which the equal sign is introduced
{{DEFAULTSORT:Equal Sign Mathematical symbols 1550s introductions 1557 beginnings Definition Assignment operations Equivalence (mathematics)
British English
British English is the set of Variety (linguistics), varieties of the English language native to the United Kingdom, especially Great Britain. More narrowly, it can refer specifically to the English language in England, or, more broadly, to ...
) or equal sign (American English
American English, sometimes called United States English or U.S. English, is the set of variety (linguistics), varieties of the English language native to the United States. English is the Languages of the United States, most widely spoken lang ...
), also known as the equality sign, is the mathematical symbol , which is used to indicate equality. In an equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
it is placed between two expressions that have the same value, or for which one studies the conditions under which they have the same value.
In Unicode
Unicode or ''The Unicode Standard'' or TUS is a character encoding standard maintained by the Unicode Consortium designed to support the use of text in all of the world's writing systems that can be digitized. Version 16.0 defines 154,998 Char ...
and ASCII
ASCII ( ), an acronym for American Standard Code for Information Interchange, is a character encoding standard for representing a particular set of 95 (English language focused) printable character, printable and 33 control character, control c ...
it has the code point
A code point, codepoint or code position is a particular position in a Table (database), table, where the position has been assigned a meaning. The table may be one dimensional (a column), two dimensional (like cells in a spreadsheet), three dime ...
U+003D. It was invented in 1557 by the Welsh mathematician Robert Recorde.
History
Prior to 16th century there was no common symbol for equality, and equality was usually expressed with a word, such as ''aequales, aequantur, esgale, faciunt, ghelijck'' or ''gleich,'' and sometimes by the abbreviated form ''aeq'', or simply and . Diophantus's use of , short for ( 'equals'), in '' Arithmetica'' () is considered one of the first uses of an equals sign. The symbol, now universally accepted in mathematics for equality, was first recorded by the Welsh mathematician Robert Recorde in '' The Whetstone of Witte'' (1557). The original form of the symbol was much wider than the present form. In his book Recorde explains his design of the "Gemowe lines" (meaning ''twin'' lines, from theLatin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
)See also geminus and Gemini.
The symbol was not immediately popular. After its introduction by Recorde, it was not used again in print until 1618 (61 years later), in an anonymous Appendix in Edward Wright's English translation of '' Descriptio'', by John Napier
John Napier of Merchiston ( ; Latinisation of names, Latinized as Ioannes Neper; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8 ...
. It was not until 1631 that it received more than general recognition in England, being adopted as the symbol for equality in three influential works, Thomas Harriot's ''Artis analyticae praxis'', William Oughtred's '' Clavis mathematicae'' and Richard Norwood's '' Trigonometria''. Later used by John Wallis, Isaac Barrow and Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
, which helped it to spread to continental Europe.
Competing symbols
There were several other competing symbols for equality, especially outside of England around the 16th and 17th centuries, and Recorde's version made no significant influence in the European continent until 1650 or 1660. In 1559 the French monk Johannes Buteo published his ''Logistica'' using the symbol for equality. In 1571 Wilhelm Xylander published an edition of Arithmetica">Diophantus' ''Arithmetica'' in which two parallel vertical lines were used for equality. This version was adopted by several prominent writers, including Giovanni Glorioso, Cardinal Michelangelo Ricci">Giovanni Camillo Glorioso">Giovanni Glorioso, Cardinal Michelangelo Ricci, and many French and Dutch mathematicians in the hundred years after, including René Descartes in 1621. A major competitor to Recorde's sign was Descartes' own symbol, introduced in his La Géométrie, ''La Géométrie'' (1637). In fact, Descartes himself used the sign for equality in a letter in 1640. Descartes does not give any reason for introducing his new symbol; however, Florian Cajori suggests it is because was also being used for a difference operation at the time. Due to the prominence of ''La Géométrie'', by 1675, Descartes' symbol gained favour over Recorde's in Europe, and most 17th-century writers on the continent either used Descartes' notation for equality or none at all. Around the turn of the 18th century, Recorde's notation gained favour rapidly. The dominating trend in mathematics of the time was differential and integral calculus. The fact that both Newton andGottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Sir Isaac Newton, with the creation of calculus in addition to ...
used Recorde's symbol led to its general adoption.
Usage in mathematics and computer programming
In mathematics, the equals sign can be used as a simple statement of fact in a specific case (""), or to create definitions (""), conditional statements (""), or to express a universal equivalence (""). The first important computer programming language to use the equals sign was the original version of Fortran, FORTRAN I, designed in 1954 and implemented in 1957. In Fortran, serves as an assignment operator: sets the value of to 2. This somewhat resembles the use of in a mathematical definition, but with different semantics: the expression following is evaluated first, and may refer to a previous value of . For example, the assignment increases the value of by 2. A rival programming-language usage was pioneered by the original version of ALGOL, which was designed in 1958 and implemented in 1960. ALGOL included a relational operator that tested for equality, allowing constructions like with essentially the same meaning of as the conditional usage in mathematics. The equals sign was reserved for this usage. Both usages have remained common in different programming languages into the early-21st century. As well as Fortran, is used for assignment in such languages as C, Perl, Python, AWK and their descendants. But is used for equality and not assignment in the Pascal family, Ada, Eiffel, APL, and other languages. A few languages, such asBASIC
Basic or BASIC may refer to:
Science and technology
* BASIC, a computer programming language
* Basic (chemistry), having the properties of a base
* Basic access authentication, in HTTP
Entertainment
* Basic (film), ''Basic'' (film), a 2003 film
...
and PL/I, have used the equals sign to mean both assignment and equality, distinguished by context. However, in most languages where has one of these meanings, a different character or, more often, a sequence of characters is used for the other meaning. Following ALGOL, most languages that use for equality use for assignment, although APL, with its special character set, uses a left-pointing arrow.
Fortran did not have an equality operator (it was only possible to compare an expression to zero, using the arithmetic IF statement) until FORTRANIV was released in 1962, since when it has used the four characters to test for equality. The language B introduced the use of with this meaning, which has been copied by its descendant C and most later languages where means assignment.
Some languages additionally feature the " spaceship operator", or three-way comparison operator, , to determine whether one value is less than, equal to, or greater than another.
Several equals signs
In some programming languages,1844 1844 will return true.
In PHP, the triple equals sign, , denotes value and type equality, meaning that not only do the two expressions evaluate to equal values, but they are also of the same data type. For instance, the expression is true, but is not, because the number 0 is an integer value whereas false is a Boolean value.
JavaScript
JavaScript (), often abbreviated as JS, is a programming language and core technology of the World Wide Web, alongside HTML and CSS. Ninety-nine percent of websites use JavaScript on the client side for webpage behavior.
Web browsers have ...
has the same semantics for , referred to as "equality without type coercion". However, in JavaScript the behavior of cannot be described by any simple consistent rules. The expression is true, but is false, even though both sides of the act the same in Boolean context. For this reason it is sometimes recommended to avoid the operator in JavaScript in favor of .
In Ruby, equality under requires both operands to be of identical type, e.g. is false. The operator is flexible and may be defined arbitrarily for any given type. For example, a value of type is a range of integers, such as . is false, since the types are different (Range vs. Integer); however is true, since on values means "inclusion in the range". Under these semantics, 1844 (1800..1899) is false, since it is interpreted to mean Integer# rather than Range#.
Other uses
Spelling
Tone letter
The equals sign is also used as a grammatical tone letter in the orthographies of Budu in the Congo-Kinshasa, in Krumen, Mwan and Dan in theIvory Coast
Ivory Coast, also known as Côte d'Ivoire and officially the Republic of Côte d'Ivoire, is a country on the southern coast of West Africa. Its capital city of Yamoussoukro is located in the centre of the country, while its largest List of ci ...
. The Unicode character used for the tone letter () is different from the mathematical symbol (U+003D).
Personal names
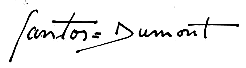 A possibly unique case of the equals sign of European usage in a person's name, specifically in a double-barreled name, was by the aviation pioneer Alberto Santos-Dumont, as he is also known not only to have often used a double hyphen resembling an equal sign between his two surnames in place of a hyphen, but also seems to have personally preferred that practice, to display equal respect for his father's French ethnicity and the Brazilian ethnicity of his mother.
Instead of a double hyphen, the equals sign is sometimes used in Japanese as a separator between names. In
A possibly unique case of the equals sign of European usage in a person's name, specifically in a double-barreled name, was by the aviation pioneer Alberto Santos-Dumont, as he is also known not only to have often used a double hyphen resembling an equal sign between his two surnames in place of a hyphen, but also seems to have personally preferred that practice, to display equal respect for his father's French ethnicity and the Brazilian ethnicity of his mother.
Instead of a double hyphen, the equals sign is sometimes used in Japanese as a separator between names. In Ojibwe
The Ojibwe (; Ojibwe writing systems#Ojibwe syllabics, syll.: ᐅᒋᐺ; plural: ''Ojibweg'' ᐅᒋᐺᒃ) are an Anishinaabe people whose homeland (''Ojibwewaki'' ᐅᒋᐺᐘᑭ) covers much of the Great Lakes region and the Great Plains, n ...
, the readily available equals sign on most keyboards is commonly used as a substitute for a double hyphen.
Linguistics
In linguistic interlinear glosses, an equals sign is conventionally used to mark clitic boundaries: the equals sign is placed between theclitic
In morphology and syntax, a clitic ( , backformed from Greek "leaning" or "enclitic"Crystal, David. ''A First Dictionary of Linguistics and Phonetics''. Boulder, CO: Westview, 1980. Print.) is a morpheme that has syntactic characteristics of a ...
and the word that the clitic is attached to.
Chemistry
Inchemical formula
A chemical formula is a way of presenting information about the chemical proportions of atoms that constitute a particular chemical compound or molecule, using chemical element symbols, numbers, and sometimes also other symbols, such as pare ...
s, the two parallel lines denoting a double bond are commonly rendered using an equals sign (hence, a triple bond is commonly rendered using a triple bar).
LGBT activism
In recent years, the equals sign has been used to symbolizeLGBT rights
Rights affecting lesbian, Gay men, gay, Bisexuality, bisexual, transgender and queer (LGBTQ) people vary greatly by country or jurisdiction—encompassing everything from the legal recognition of same-sex marriage to the Capital punishmen ...
. It has been used since 1995 by the Human Rights Campaign, which lobbies for marriage equality, and subsequently by the United Nations Free & Equal, which promotes LGBT rights at the United Nations.
Telegrams and Telex
InMorse code
Morse code is a telecommunications method which Character encoding, encodes Written language, text characters as standardized sequences of two different signal durations, called ''dots'' and ''dashes'', or ''dits'' and ''dahs''. Morse code i ...
the equals sign is encoded by the letters B (-...) and T (-) run together (-...-). The letters BT stand for Break Text, and are put between paragraphs, or groups of paragraphs in messages sent via Telex
Telex is a telecommunication
Telecommunication, often used in its plural form or abbreviated as telecom, is the transmission of information over a distance using electronic means, typically through cables, radio waves, or other communica ...
, a standardised tele-typewriter. The sign, used to mean Break Text, is given at the end of a telegram
Telegraphy is the long-distance transmission of messages where the sender uses symbolic codes, known to the recipient, rather than a physical exchange of an object bearing the message. Thus flag semaphore is a method of telegraphy, whereas pi ...
to separate the text of the message from the signature.
Related symbols
Approximately equal
Symbols used to denote items that are '' approximately equal'' include the following: * ≈ (,LaTeX
Latex is an emulsion (stable dispersion) of polymer microparticles in water. Latices are found in nature, but synthetic latices are common as well.
In nature, latex is found as a wikt:milky, milky fluid, which is present in 10% of all floweri ...
''\approx'')
* ≃ (, LaTeX ''\simeq''), a combination of and , also used to indicate asymptotic equality
* ≅ (, LaTeX ''\cong''), another combination of ≈ and =, which is also sometimes used to indicate isomorphism or congruence
* (, LaTeX ''\sim''), which is also sometimes used to indicate proportionality or similarity, being related by an equivalence relation, or to indicate that a random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathema ...
is distributed according to a specific probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
(see also tilde), or alternatively between two quantities to indicate they are of the same order of magnitude.
* ∽ (, LaTeX ''\backsim''), which is also used to indicate proportionality
* ≐ (, LaTeX ''\doteq''), which can also be used to represent the approach of a variable to a limit
* ≒ (, LaTeX ''\fallingdotseq''), commonly used in Japan, Taiwan, and Korea.
* ≓ (, LaTeX ''\risingdotseq'')
In some areas of East Asia, such as Japan, "≒" is used to mean "the two terms are almost equal", but in other areas and specialized literature such as mathematics, "≃" is often used. In addition to its mathematical meaning, it is sometimes used in Japanese sentences with the intention of "almost the same".
Not equal
The symbol used to denote inequation (when items are not equal) is a slashed equal sign (U+2260). InLaTeX
Latex is an emulsion (stable dispersion) of polymer microparticles in water. Latices are found in nature, but synthetic latices are common as well.
In nature, latex is found as a wikt:milky, milky fluid, which is present in 10% of all floweri ...
, this is done with the "\neq" command.
Most programming languages, limiting themselves to the 7-bit ASCII character set and typeable characters, use , , , or to represent their Boolean inequality operator.
Identity
The triple bar symbol (U+2261, LaTeX ''\equiv'') is often used to indicate an identity, adefinition
A definition is a statement of the meaning of a term (a word, phrase, or other set of symbols). Definitions can be classified into two large categories: intensional definitions (which try to give the sense of a term), and extensional definitio ...
(which can also be represented by or ), or a congruence relation in modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic operations for integers, other than the usual ones from elementary arithmetic, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to mo ...
. Also, in chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, the triple bar can be used to represent a triple bond between atoms.
Isomorphism
The symbol is often used to indicate isomorphic algebraic structures or congruent geometric figures.In logic
Equality oftruth value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values ('' true'' or '' false''). Truth values are used in ...
s (through bi-implication or logical equivalence
In logic and mathematics, statements p and q are said to be logically equivalent if they have the same truth value in every model. The logical equivalence of p and q is sometimes expressed as p \equiv q, p :: q, \textsfpq, or p \iff q, depending ...
), may be denoted by various symbols including , , and .In geometry
The symbol (LaTeX \bumpeq) is used to show two directed line segments have the same length and direction, equipollence.Other related symbols
Additional precomposed symbols withcode point
A code point, codepoint or code position is a particular position in a Table (database), table, where the position has been assigned a meaning. The table may be one dimensional (a column), two dimensional (like cells in a spreadsheet), three dime ...
s in Unicode for notations related to the equal sign include the following:
* ≌ ()
* ≔ () ( used to define a symbol or assign a variable)
* ≕ () (defines the symbol on the right-hand side)
* ≖ ()
* ≗ ()
* ≘ ()
* ≙ () (the left-hand side is an estimator for the right-hand side)
* ≚ ()
* ≛ ()
* ≜ () ( used to define a symbol)
* ≞ ()
* ≟ ()
* ⩴ () (see also Backus–Naur form
In computer science, Backus–Naur form (BNF, pronounced ), also known as Backus normal form, is a notation system for defining the Syntax (programming languages), syntax of Programming language, programming languages and other Formal language, for ...
for )
* ⩵ ()
* ⩶ ()
Incorrect usage
The equals sign is sometimes used incorrectly within a mathematical argument to connect math steps in a non-standard way, rather than to show equality (especially by early mathematics students). For example, if one were finding the sum, step by step, of the numbers 1, 2, 3, 4, and 5, one might incorrectly write :1 + 2 = 3 + 3 = 6 + 4 = 10 + 5 = 15. Structurally, this is shorthand for :( 1 + 2 = 3) + 3 = 6+ 4 = 10) + 5 = 15, but the notation is incorrect, because each part of the equality has a different value. If interpreted strictly as it says, it would imply that :3 = 6 = 10 = 15 = 15. A correct version of the argument would be :1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, 10 + 5 = 15. This difficulty results from subtly different uses of the sign in education. In early, arithmetic-focused grades, the equals sign may be ''operational''; like the equal button on an electronic calculator, it demands the result of a calculation. Starting in algebra courses, the sign takes on a ''relational'' meaning of equality between two calculations. Confusion between the two uses of the sign sometimes persists at the university level.Encodings
* Related symbols * * * * * * * * *See also
* 2 + 2 = 5 * Double hyphen *Equality (mathematics)
In mathematics, equality is a relationship between two quantities or Expression (mathematics), expressions, stating that they have the same value, or represent the same mathematical object. Equality between and is written , and read " equa ...
* Logical equality
* Plus and minus signs
The plus sign () and the minus sign () are Glossary of mathematical symbols, mathematical symbols used to denote sign (mathematics), positive and sign (mathematics), negative functions, respectively. In addition, the symbol represents the oper ...
Notes
References
* * Boyer, C. B.: ''A History of Mathematics'', 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 (1991 pbk ed. )External links
Earliest Uses of Symbols of Relation
{{DEFAULTSORT:Equal Sign Mathematical symbols 1550s introductions 1557 beginnings Definition Assignment operations Equivalence (mathematics)