Eddington–Finkelstein coordinates on:
[Wikipedia]
[Google]
[Amazon]
In
 The
The
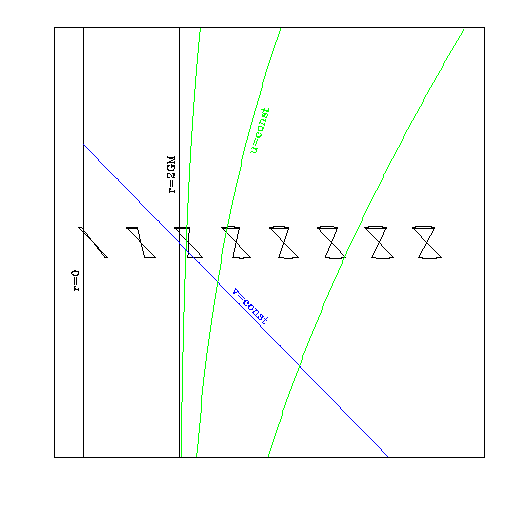 The Eddington–Finkelstein coordinates are still incomplete and can be extended. For example, the outward traveling timelike geodesics defined by (with ''τ'' the proper time)
:
:
has ''v''(''τ'') → −∞ as ''τ'' → 2''GM''. Ie, this timelike geodesic has a finite proper length into the past where it comes out of the horizon (''r'' = 2''GM'') when ''v'' becomes minus infinity. The regions for finite ''v'' and ''r'' < 2''GM'' is a different region from finite ''u'' and ''r'' < 2''GM''. The horizon ''r'' = 2''GM'' and finite ''v'' (the black hole horizon) is different from that with ''r'' = 2''GM'' and finite ''u ''(the
The Eddington–Finkelstein coordinates are still incomplete and can be extended. For example, the outward traveling timelike geodesics defined by (with ''τ'' the proper time)
:
:
has ''v''(''τ'') → −∞ as ''τ'' → 2''GM''. Ie, this timelike geodesic has a finite proper length into the past where it comes out of the horizon (''r'' = 2''GM'') when ''v'' becomes minus infinity. The regions for finite ''v'' and ''r'' < 2''GM'' is a different region from finite ''u'' and ''r'' < 2''GM''. The horizon ''r'' = 2''GM'' and finite ''v'' (the black hole horizon) is different from that with ''r'' = 2''GM'' and finite ''u ''(the
general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
, Eddington–Finkelstein coordinates are a pair of coordinate systems for a Schwarzschild geometry (e.g. a spherically symmetric black hole) which are adapted to radial null geodesic
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational forces is a particular type of geodesic. In other words, a fre ...
s. Null geodesics are the worldline
The world line (or worldline) of an object is the path that an object traces in 4-dimensional spacetime. It is an important concept in modern physics, and particularly theoretical physics.
The concept of a "world line" is distinguished from con ...
s of photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they a ...
s; radial ones are those that are moving directly towards or away from the central mass. They are named for Arthur Stanley Eddington
Sir Arthur Stanley Eddington (28 December 1882 – 22 November 1944) was an English astronomer, physicist, and mathematician. He was also a philosopher of science and a populariser of science. The Eddington limit, the natural limit to the lumi ...
and David Finkelstein
David Ritz Finkelstein (July 19, 1929 – January 24, 2016) was an emeritus professor of physics at the Georgia Institute of Technology.
Biography
Born in New York City, Finkelstein obtained his Ph.D. in physics at the Massachusetts Institute ...
. Although they appear to have inspired the idea, neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein. Most influentially, Misner, Thorne and Wheeler, in their book '' Gravitation'', refer to the null coordinates by that name.
In these coordinate systems, outward (inward) traveling radial light rays (which each follow a null geodesic) define the surfaces of constant "time", while the radial coordinate is the usual area coordinate so that the surfaces of rotation symmetry have an area of . One advantage of this coordinate system is that it shows that the apparent singularity at the Schwarzschild radius
The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein's field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteris ...
is only a coordinate singularity A coordinate singularity occurs when an apparent singularity or discontinuity occurs in one coordinate frame that can be removed by choosing a different frame.
An example is the apparent (longitudinal) singularity at the 90 degree latitude in sph ...
and is not a true physical singularity. While this fact was recognized by Finkelstein, it was not recognized (or at least not commented on) by Eddington, whose primary purpose was to compare and contrast the spherically symmetric solutions in Whitehead's theory of gravitation and Einstein's version of the theory of relativity.
Schwarzschild metric
 The
The Schwarzschild coordinates In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of ''nested round spheres''. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coord ...
are , and in these coordinates the Schwarzschild metric is well known:
:
where
:
is the standard Riemannian metric of the unit 2-sphere.
Note the conventions being used here are the metric signature
In mathematics, the signature of a metric tensor ''g'' (or equivalently, a real quadratic form thought of as a real symmetric bilinear form on a finite-dimensional vector space) is the number (counted with multiplicity) of positive, negative and ...
of (− + + +) and the natural units
In physics, natural units are physical units of measurement in which only universal physical constants are used as defining constants, such that each of these constants acts as a coherent unit of a quantity. For example, the elementary charge ma ...
where ''c'' = 1 is the dimensionless speed of light, ''G'' the gravitational constant, and ''M'' is the characteristic mass of the Schwarzschild geometry.
Tortoise coordinate
Eddington–Finkelstein coordinates are founded upon the tortoise coordinate – a name that comes from one ofZeno of Elea
Zeno of Elea (; grc, Ζήνων ὁ Ἐλεᾱ́της; ) was a pre-Socratic Greek philosopher of Magna Graecia and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known ...
's paradoxes on an imaginary footrace between "swift-footed" Achilles and a tortoise.
The tortoise coordinate is defined:
:
so as to satisfy:
:
The tortoise coordinate approaches as approaches the Schwarzschild radius .
When some probe (such as a light ray or an observer) approaches a black hole event horizon, its Schwarzschild time coordinate grows infinite. The outgoing null rays in this coordinate system have an infinite change in ''t'' on travelling out from the horizon. The tortoise coordinate is intended to grow infinite at the appropriate rate such as to cancel out this singular behaviour in coordinate systems constructed from it.
The increase in the time coordinate to infinity as one approaches the event horizon is why information could never be received back from any probe that is sent through such an event horizon. This is despite the fact that the probe itself can nonetheless travel past the horizon. It is also why the space-time metric of the black hole, when expressed in Schwarzschild coordinates, becomes singular at the horizon – and thereby fails to be able to fully chart the trajectory of an infalling probe.
Metric
The ingoing Eddington–Finkelstein coordinates are obtained by replacing the coordinate ''t'' with the new coordinate ''''. In these coordinates, the Schwarzschild metric can be written as : where again is the standard Riemannian metric on the unit radius 2-sphere. Likewise, the outgoing Eddington–Finkelstein coordinates are obtained by replacing ''t'' with the null coordinate ''''. The metric is then given by : In both these coordinate systems the metric is explicitly non-singular at the Schwarzschild radius (even though one component vanishes at this radius, the determinant of the metric is still non-vanishing and the inverse metric has no terms which diverge there.) Note that for radial null rays, ''v=const'' or ''=const'' or equivalently ''=const'' or ''u=const'' we have ''dv/dr'' and ''du/dr'' approach 0 and ±2 at large ''r'', not ±1 as one might expect if one regarded ''u'' or ''v'' as "time". When plotting Eddington–Finkelstein diagrams, surfaces of constant ''u'' or ''v'' are usually drawn as cones, with ''u'' or ''v'' constant lines drawn as sloping at 45 degree rather than as planes (see for instance Box 31.2 of MTW). Some sources instead take , corresponding to planar surfaces in such diagrams. In terms of this the metric becomes : which is Minkowskian at large ''r''. (This was the coordinate time and metric that both Eddington and Finkelstein presented in their papers.) The Eddington–Finkelstein coordinates are still incomplete and can be extended. For example, the outward traveling timelike geodesics defined by (with ''τ'' the proper time)
:
:
has ''v''(''τ'') → −∞ as ''τ'' → 2''GM''. Ie, this timelike geodesic has a finite proper length into the past where it comes out of the horizon (''r'' = 2''GM'') when ''v'' becomes minus infinity. The regions for finite ''v'' and ''r'' < 2''GM'' is a different region from finite ''u'' and ''r'' < 2''GM''. The horizon ''r'' = 2''GM'' and finite ''v'' (the black hole horizon) is different from that with ''r'' = 2''GM'' and finite ''u ''(the
The Eddington–Finkelstein coordinates are still incomplete and can be extended. For example, the outward traveling timelike geodesics defined by (with ''τ'' the proper time)
:
:
has ''v''(''τ'') → −∞ as ''τ'' → 2''GM''. Ie, this timelike geodesic has a finite proper length into the past where it comes out of the horizon (''r'' = 2''GM'') when ''v'' becomes minus infinity. The regions for finite ''v'' and ''r'' < 2''GM'' is a different region from finite ''u'' and ''r'' < 2''GM''. The horizon ''r'' = 2''GM'' and finite ''v'' (the black hole horizon) is different from that with ''r'' = 2''GM'' and finite ''u ''(the white hole
In general relativity, a white hole is a hypothetical region of spacetime and singularity that cannot be entered from the outside, although energy-matter, light and information can escape from it. In this sense, it is the reverse of a black ho ...
horizon) .
The metric in Kruskal–Szekeres coordinates
In general relativity, Kruskal–Szekeres coordinates, named after Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole. These coordinates have the advantage that they cover the entire space ...
covers all of the extended Schwarzschild spacetime in a single coordinate system. Its chief disadvantage is that in those coordinates the metric depends on both the time and space coordinates. In Eddington–Finkelstein, as in Schwarzschild coordinates, the metric is independent of the "time" (either ''t'' in Schwarzschild, or ''u'' or ''v'' in the various Eddington–Finkelstein coordinates), but none of these cover the complete spacetime.
The Eddington–Finkelstein coordinates have some similarity to the Gullstrand–Painlevé coordinates in that both are time independent, and penetrate (are regular across) either the future (black hole) or the past (white hole) horizons. Both are not diagonal (the hypersurfaces of constant "time" are not orthogonal to the hypersurfaces of constant ''r''.) The latter have a flat spatial metric, while the former's spatial ("time" constant) hypersurfaces are null and have the same metric as that of a null cone in Minkowski space ( in flat spacetime).
See also
*Schwarzschild coordinates In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of ''nested round spheres''. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coord ...
*Kruskal–Szekeres coordinates
In general relativity, Kruskal–Szekeres coordinates, named after Martin Kruskal and George Szekeres, are a coordinate system for the Schwarzschild geometry for a black hole. These coordinates have the advantage that they cover the entire space ...
* Lemaître coordinates
* Gullstrand–Painlevé coordinates
* Vaidya metric
References
{{DEFAULTSORT:Eddington-Finkelstein Coordinates Coordinate charts in general relativity