Dual polyhedron on:
[Wikipedia]
[Google]
[Amazon]
 In
In
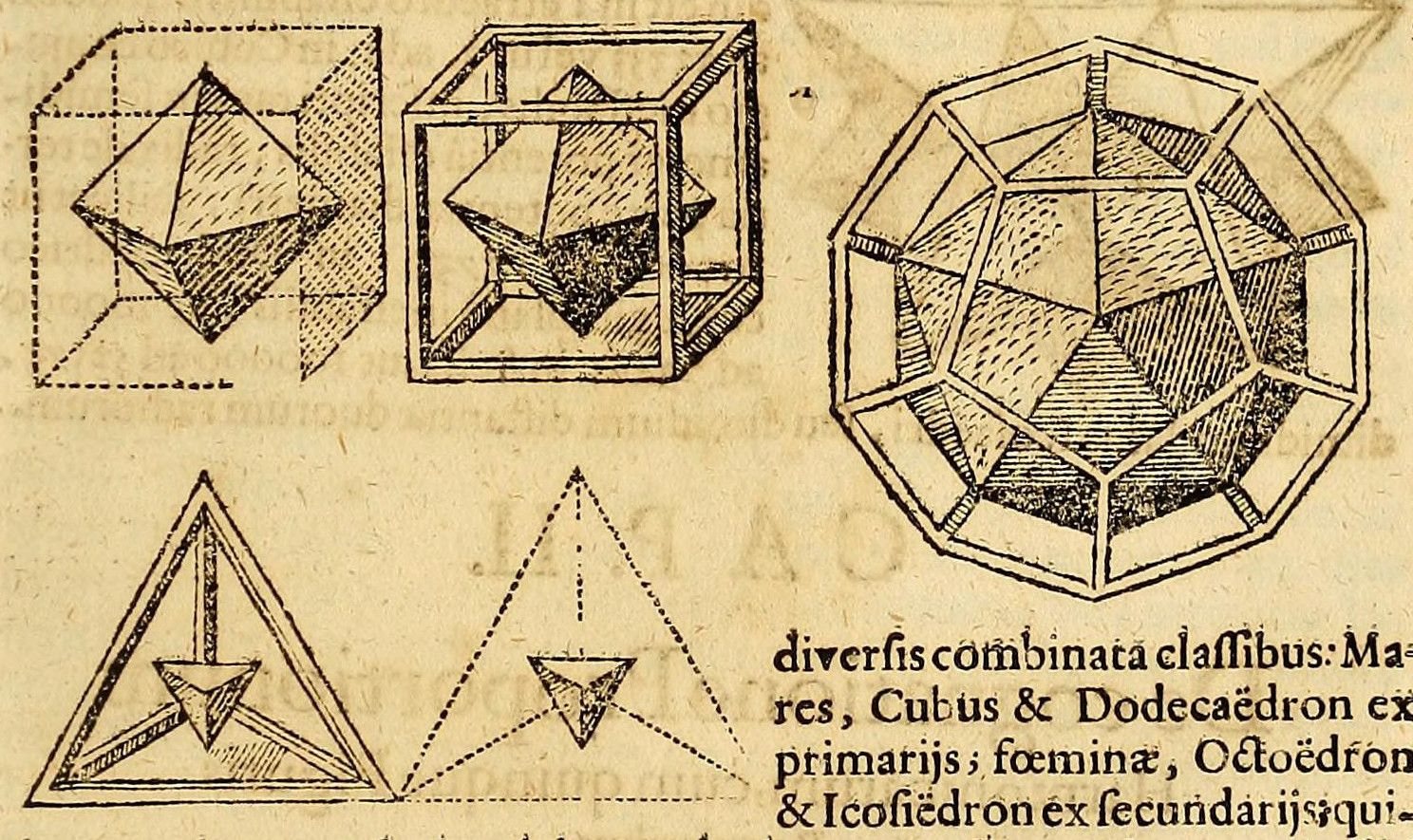 There are many kinds of duality. The kinds most relevant to elementary polyhedra are polar reciprocity and topological or abstract duality.
There are many kinds of duality. The kinds most relevant to elementary polyhedra are polar reciprocity and topological or abstract duality.
 Any convex polyhedron can be distorted into a
Any convex polyhedron can be distorted into a

 The primary class of self-dual polytopes are
The primary class of self-dual polytopes are
 In
In geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ...
, every polyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
is associated with a second dual structure, where the vertices of one correspond to the faces
The face is the front of an animal's head that features the eyes, nose and mouth, and through which animals express many of their emotions. The face is crucial for human identity, and damage such as scarring or developmental deformities may affe ...
of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
Duality preserves the symmetries of a polyhedron. Therefore, for many classes of polyhedra defined by their symmetries, the duals belong to a corresponding symmetry class. For example, the regular polyhedrathe (convex) Platonic solid
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (all angles congruent and all e ...
s and (star) Kepler–Poinsot polyhedraform dual pairs, where the regular tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all th ...
is self-dual. The dual of an isogonal polyhedron (one in which any two vertices are equivalent under symmetries of the polyhedron) is an isohedral
In geometry, a tessellation of dimension (a plane tiling) or higher, or a polytope of dimension (a polyhedron) or higher, is isohedral or face-transitive if all its faces are the same. More specifically, all faces must be not merely congruent ...
polyhedron (one in which any two faces are equivalent .., and vice versa. The dual of an isotoxal polyhedron (one in which any two edges are equivalent .. is also isotoxal.
Duality is closely related to ''polar reciprocity'', a geometric transformation that, when applied to a convex polyhedron, realizes the dual polyhedron as another convex polyhedron.
Kinds of duality
 There are many kinds of duality. The kinds most relevant to elementary polyhedra are polar reciprocity and topological or abstract duality.
There are many kinds of duality. The kinds most relevant to elementary polyhedra are polar reciprocity and topological or abstract duality.
Polar reciprocation
InEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
, the dual of a polyhedron is often defined in terms of polar reciprocation
In geometry, a pole and polar are respectively a point and a line that have a unique reciprocal relationship with respect to a given conic section.
Polar reciprocation in a given circle is the transformation of each point in the plane into it ...
about a sphere. Here, each vertex (pole) is associated with a face plane (polar plane or just polar) so that the ray from the center to the vertex is perpendicular to the plane, and the product of the distances from the center to each is equal to the square of the radius.
When the sphere has radius and is centered at the origin (so that it is defined by the equation ), then the polar dual of a convex polyhedron is defined as
where denotes the standard dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alge ...
of and .
Typically when no sphere is specified in the construction of the dual, then the unit sphere is used, meaning in the above definitions.
For each face plane of described by the linear equation
the corresponding vertex of the dual polyhedron will have coordinates . Similarly, each vertex of corresponds to a face plane of , and each edge line of corresponds to an edge line of . The correspondence between the vertices, edges, and faces of and reverses inclusion. For example, if an edge of contains a vertex, the corresponding edge of will be contained in the corresponding face.
For a polyhedron with a center of symmetry, it is common to use a sphere centered on this point, as in the Dorman Luke construction (mentioned below). Failing that, for a polyhedron with a circumscribed sphere, inscribed sphere, or midsphere (one with all edges as tangents), this can be used. However, it is possible to reciprocate a polyhedron about any sphere, and the resulting form of the dual will depend on the size and position of the sphere; as the sphere is varied, so too is the dual form. The choice of center for the sphere is sufficient to define the dual up to similarity.
If a polyhedron in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean ...
has a face plane, edge line, or vertex lying on the center of the sphere, the corresponding element of its dual will go to infinity. Since Euclidean space never reaches infinity, the projective equivalent, called extended Euclidean space, may be formed by adding the required 'plane at infinity'. Some theorists prefer to stick to Euclidean space and say that there is no dual. Meanwhile, found a way to represent these infinite duals, in a manner suitable for making models (of some finite portion).
The concept of ''duality'' here is closely related to the duality in projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, ...
, where lines and edges are interchanged. Projective polarity works well enough for convex polyhedra. But for non-convex figures such as star polyhedra, when we seek to rigorously define this form of polyhedral duality in terms of projective polarity, various problems appear.
Because of the definitional issues for geometric duality of non-convex polyhedra, argues that any proper definition of a non-convex polyhedron should include a notion of a dual polyhedron.
Canonical duals
 Any convex polyhedron can be distorted into a
Any convex polyhedron can be distorted into a canonical form
In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an ...
, in which a unit midsphere
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every convex po ...
(or intersphere) exists tangent to every edge, and such that the average position of the points of tangency is the center of the sphere. This form is unique up to congruences.
If we reciprocate such a canonical polyhedron about its midsphere, the dual polyhedron will share the same edge-tangency points, and thus will also be canonical. It is the canonical dual, and the two together form a canonical dual compound.
Dorman Luke construction
For auniform polyhedron
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent.
Uniform polyhedra may be regular (if also ...
, each face of the dual polyhedron may be derived from the original polyhedron's corresponding vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or vertex of a polyhedron. Mark a point somewhere along each connected edge. Draw line ...
by using the Dorman Luke construction.
Topological duality
Even when a pair of polyhedra cannot be obtained by reciprocation from each other, they may be called duals of each other as long as the vertices of one correspond to the faces of the other, and the edges of one correspond to the edges of the other, in an incidence-preserving way. Such pairs of polyhedra are still topologically or abstractly dual. The vertices and edges of a convex polyhedron form agraph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
(the 1-skeleton
In mathematics, particularly in algebraic topology, the of a topological space presented as a simplicial complex (resp. CW complex) refers to the subspace that is the union of the simplices of (resp. cells of ) of dimensions In other wo ...
of the polyhedron), embedded on the surface of the polyhedron (a topological sphere). This graph can be projected to form a Schlegel diagram
In geometry, a Schlegel diagram is a projection of a polytope from \mathbb^d into \mathbb^ through a point just outside one of its facets. The resulting entity is a polytopal subdivision of the facet in \mathbb^ that, together with the orig ...
on a flat plane. The graph formed by the vertices and edges of the dual polyhedron is the dual graph
In the mathematical discipline of graph theory, the dual graph of a plane graph is a graph that has a vertex for each face of . The dual graph has an edge for each pair of faces in that are separated from each other by an edge, and a self-lo ...
of the original graph.
More generally, for any polyhedron whose faces form a closed surface, the vertices and edges of the polyhedron form a graph embedded on this surface, and the vertices and edges of the (abstract) dual polyhedron form the dual graph of the original graph.
An abstract polyhedron is a certain kind of partially ordered set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a bina ...
(poset) of elements, such that incidences, or connections, between elements of the set correspond to incidences between elements (faces, edges, vertices) of a polyhedron. Every such poset has a dual poset, formed by reversing all of the order relations. If the poset is visualized as a Hasse diagram
In order theory, a Hasse diagram (; ) is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set ''(S, ≤)'' one represents ...
, the dual poset can be visualized simply by turning the Hasse diagram upside down.
Every geometric polyhedron corresponds to an abstract polyhedron in this way, and has an abstract dual polyhedron. However, for some types of non-convex geometric polyhedra, the dual polyhedra may not be realizable geometrically.
Self-dual polyhedra
Topologically, a self-dual polyhedron is one whose dual has exactly the same connectivity between vertices, edges and faces. Abstractly, they have the sameHasse diagram
In order theory, a Hasse diagram (; ) is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction. Concretely, for a partially ordered set ''(S, ≤)'' one represents ...
.
A geometrically self-dual polyhedron is not only topologically self-dual, but its polar reciprocal about a certain point, typically its centroid, is a similar figure. For example, the dual of a regular tetrahedron is another regular tetrahedron, reflected through the origin.
Every polygon (that is, a two-dimensional polyhedron) is topologically self-dual, since it has the same number of vertices as edges, and these are switched by duality. But it is not necessarily self-dual (up to rigid motion, for instance). Every polygon has a regular form which is geometrically self-dual about its intersphere: all angles are congruent, as are all edges, so under duality these congruences swap.
Similarly, every topologically self-dual convex polyhedron can be realized by an equivalent geometrically self-dual polyhedron, its canonical polyhedron
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every convex po ...
, reciprocal about the center of the midsphere
In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every convex po ...
.
There are infinitely many geometrically self-dual polyhedra. The simplest infinite family are the canonical pyramids of ''n'' sides. Another infinite family, elongated pyramids, consists of polyhedra that can be roughly described as a pyramid sitting on top of a prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
(with the same number of sides). Adding a frustum (pyramid with the top cut off) below the prism generates another infinite family, and so on.
There are many other convex, self-dual polyhedra. For example, there are 6 different ones with 7 vertices, and 16 with 8 vertices.
A self-dual non-convex icosahedron with hexagonal faces was identified by Brückner in 1900.Brückner, M.; ''Vielecke und Vielflache: Theorie und Geschichte'', Teubner, Leipzig, 1900. Other non-convex self-dual polyhedra have been found, under certain definitions of non-convex polyhedra and their duals.
Dual polytopes and tessellations
Duality can be generalized to ''n''-dimensional space and dualpolytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an ...
s; in two dimension these are called dual polygons.
The vertices of one polytope correspond to the (''n'' − 1)-dimensional elements, or facets, of the other, and the ''j'' points that define a (''j'' − 1)-dimensional element will correspond to ''j'' hyperplanes that intersect to give a (''n'' − ''j'')-dimensional element. The dual of an ''n''-dimensional tessellation or honeycomb
A honeycomb is a mass of hexagonal prismatic wax cells built by honey bees in their nests to contain their larvae and stores of honey and pollen.
Beekeepers may remove the entire honeycomb to harvest honey. Honey bees consume about of honey ...
can be defined similarly.
In general, the facets of a polytope's dual will be the topological duals of the polytope's vertex figures. For the polar reciprocals of the regular and uniform
A uniform is a variety of clothing worn by members of an organization while participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency services, ...
polytopes, the dual facets will be polar reciprocals of the original's vertex figure. For example, in four dimensions, the vertex figure of the 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also known as the C600, hexacosichoron and hexacosihedroid. It is also called a tetraplex (abbreviated from ...
is the icosahedron; the dual of the 600-cell is the 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hec ...
, whose facets are dodecahedra
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagon ...
, which are the dual of the icosahedron.
Self-dual polytopes and tessellations

 The primary class of self-dual polytopes are
The primary class of self-dual polytopes are regular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. All its elements or -faces (for all , where is the dimension of the polytope) — cells, ...
s with palindromic
A palindrome is a word, number, phrase, or other sequence of symbols that reads the same backwards as forwards, such as the words ''madam'' or ''racecar'', the date and time ''11/11/11 11:11,'' and the sentence: "A man, a plan, a canal – Pana ...
Schläfli symbols. All regular polygons, are self-dual, polyhedra
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
of the form , 4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), an ...
s of the form , 5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by ( 4-polytope) facets, pairs of which share a polyhedral cell.
Definition
A 5-polytope is a closed five-dimensional figure with vertic ...
s of the form , etc.
The self-dual regular polytopes are:
* All regular polygon
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be either convex, star or skew. In the limit, a sequence ...
s, .
* Regular tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all th ...
:
* In general, all regular ''n''- simplexes,
* The regular 24-cell
In geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid, o ...
in 4 dimensions, .
* The great 120-cell and the grand stellated 120-cell
The self-dual (infinite) regular Euclidean honeycombs are:
* Apeirogon:
* Square tiling
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of meaning it has 4 squares around every vertex.
Conway called it a quadrille.
The internal angle of th ...
:
* Cubic honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb) in Euclidean 3-space made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a r ...
:
* In general, all regular ''n''-dimensional Euclidean hypercubic honeycombs: .
The self-dual (infinite) regular hyperbolic
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry.
The following phenomena are described as ''hyperbolic'' because they ...
honeycombs are:
* Compact hyperbolic tilings: , , ... .
* Paracompact hyperbolic tiling:
* Compact hyperbolic honeycombs: , , and
* Paracompact hyperbolic honeycombs: , , , and
See also
*Conway polyhedron notation
In geometry, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
Conway and Hart extended the idea of using o ...
* Dual polygon
* Self-dual graph
* Self-dual polygon
References
Notes
Bibliography
*. *. *. *. *. * . *.External links
* * * {{DEFAULTSORT:Dual Polyhedron PolyhedraPolyhedron
In geometry, a polyhedron (plural polyhedra or polyhedrons; ) is a three-dimensional shape with flat polygonal faces, straight edges and sharp corners or vertices.
A convex polyhedron is the convex hull of finitely many points, not all on ...
Polytopes