Deltahedron on:
[Wikipedia]
[Google]
[Amazon]
A deltahedron is a
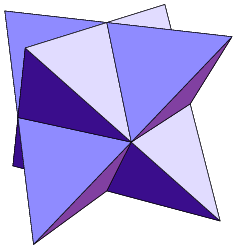 A ''non-convex deltahedron'' is a deltahedron that does not possess convexity, thus it has either coplanar faces or collinear edges. There are infinitely many non-convex deltahedra. Some examples are stella octangula, the third stellation of a regular icosahedron, and Boerdijk–Coxeter helix.
There are subclasses of non-convex deltahedra. shows that they may be discovered by finding the number of varying vertex's ''types''. A set of vertices is considered the same type as long as there are subgroups of the polyhedron's same group transitive on the set. Cundy shows that the great icosahedron is the only non-convex deltahedron with a single type of vertex. There are seventeen non-convex deltahedra with two types of vertex, and soon the other eleven deltahedra were later added by , Other subclasses are the isohedral deltahedron that was later discovered by both and , and the ''spiral deltahedron'' constructed by the strips of equilateral triangles was discovered by .
A ''non-convex deltahedron'' is a deltahedron that does not possess convexity, thus it has either coplanar faces or collinear edges. There are infinitely many non-convex deltahedra. Some examples are stella octangula, the third stellation of a regular icosahedron, and Boerdijk–Coxeter helix.
There are subclasses of non-convex deltahedra. shows that they may be discovered by finding the number of varying vertex's ''types''. A set of vertices is considered the same type as long as there are subgroups of the polyhedron's same group transitive on the set. Cundy shows that the great icosahedron is the only non-convex deltahedron with a single type of vertex. There are seventeen non-convex deltahedra with two types of vertex, and soon the other eleven deltahedra were later added by , Other subclasses are the isohedral deltahedron that was later discovered by both and , and the ''spiral deltahedron'' constructed by the strips of equilateral triangles was discovered by .
polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
whose faces are all equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
s. The deltahedron was named by Martyn Cundy, after the Greek capital letter delta
Delta commonly refers to:
* Delta (letter) (Δ or δ), the fourth letter of the Greek alphabet
* D (NATO phonetic alphabet: "Delta"), the fourth letter in the Latin alphabet
* River delta, at a river mouth
* Delta Air Lines, a major US carrier ...
resembling a triangular shape Δ.
Deltahedra can be categorized by the property of convexity. The simplest convex deltahedron is the regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
, a pyramid with four equilateral triangles. There are eight convex deltahedra, which can be used in the applications of chemistry as in the polyhedral skeletal electron pair theory and chemical compound
A chemical compound is a chemical substance composed of many identical molecules (or molecular entities) containing atoms from more than one chemical element held together by chemical bonds. A molecule consisting of atoms of only one element ...
s. There are infinitely many concave deltahedra.
Strictly convex deltahedron
A polyhedron is said to be ''convex'' if a line between any two of its vertices lies either within its interior or on its boundary, and additionally, if no two faces arecoplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
(lying in the same plane) and no two edges are collinear
In geometry, collinearity of a set of Point (geometry), points is the property of their lying on a single Line (geometry), line. A set of points with this property is said to be collinear (sometimes spelled as colinear). In greater generality, t ...
(segments of the same line), it can be considered as being strictly convex.
Of the eight convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
deltahedra, three are Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
s and five are Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s. They are:
* regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
, a pyramid with four equilateral triangles, one of which can be considered the base.
* triangular bipyramid, regular octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyh ...
, and pentagonal bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an ...
; bipyramid
In geometry, a bipyramid, dipyramid, or double pyramid is a polyhedron formed by fusing two Pyramid (geometry), pyramids together base (geometry), base-to-base. The polygonal base of each pyramid must therefore be the same, and unless otherwise ...
s with six, eight, and ten equilateral triangles, respectively. They are constructed by identical pyramids base-to-base.
* gyroelongated square bipyramid and regular icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting ...
are constructed by attaching two pyramids onto a square antiprism or pentagonal antiprism, respectively, such that they have sixteen and twenty triangular faces.
* triaugmented triangular prism, constructed by attaching three square pyramids onto the square face of a triangular prism, such that it has fourteen triangular faces.
* snub disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siame ...
, with twelve triangular faces, constructed by involving two regular hexagons in the following order: these hexagons may form a bipyramid in degeneracy, separating them into two parts along a coinciding diagonal, pressing inward on the end of diagonal, rotating one of them in 90°, and rejoining them together.
The number of possible convex deltahedrons was given by , using the fact that multiplying the number of faces by three results in each edge is shared by two faces, by which substituting this to Euler's polyhedron formula. In addition, it may show that a polyhedron with eighteen equilateral triangles is mathematically possible, although it is impossible to construct it geometrically. Rausenberger named these solids as the ''convex pseudoregular polyhedra''.
Summarizing the examples above, the deltahedra can be conclusively defined as the class of polyhedra whose faces are equilateral triangle
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the ...
s. Another definition by is similar to the previous one, in which he was interested in the shapes of holes left in irregular close-packed arrangements of spheres. It is stated as a convex polyhedron with equilateral triangular faces that can be formed by the centers of a collection of congruent spheres, whose tangencies represent polyhedron edges, and such that there is no room to pack another sphere inside the cage created by this system of spheres. Because of this restriction, some polyhedrons may not be included as a deltahedron: the triangular bipyramid (as forming two tetrahedral holes rather than a single hole), pentagonal bipyramid (because the spheres for its apexes interpenetrate, so it cannot occur in sphere packings), and regular icosahedron (because it has interior room for another sphere).
Most convex deltahedra can be found in the study of chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
. For example, they are categorized as the ''closo'' polyhedron in the study of polyhedral skeletal electron pair theory. Other applications of deltahedra—excluding the regular icosahedron—are the visualization of an atom cluster surrounding a central atom as a polyhedron in the study of chemical compounds
A chemical compound is a chemical substance composed of many identical molecules (or molecular entities) containing atoms from more than one chemical element held together by chemical bonds. A molecule consisting of atoms of only one element ...
: regular tetrahedron represents the tetrahedral molecular geometry
In a tetrahedral molecular geometry, a central atom is located at the center with four substituents that are located at the corners of a tetrahedron. The bond angles are arccos(−) = 109.4712206...° ≈ 109.5° when all four substituents are ...
, triangular bipyramid represents trigonal bipyramidal molecular geometry, regular octahedron represents the octahedral molecular geometry
In chemistry, octahedral molecular geometry, also called square bipyramidal, describes the shape of compounds with six atoms or groups of atoms or ligands symmetrically arranged around a central atom, defining the vertices of an octahedron. The o ...
, pentagonal bipyramid represents the pentagonal bipyramidal molecular geometry, gyroelongated square bipyramid represents the bicapped square antiprismatic molecular geometry, triaugmented triangular prism represents the tricapped trigonal prismatic molecular geometry, and snub disphenoid represents the dodecahedral molecular geometry. The regular icosahedron along with some other deltahedra appears in the geometry of boron hydride clusters.
Non-convex deltahedron
 A ''non-convex deltahedron'' is a deltahedron that does not possess convexity, thus it has either coplanar faces or collinear edges. There are infinitely many non-convex deltahedra. Some examples are stella octangula, the third stellation of a regular icosahedron, and Boerdijk–Coxeter helix.
There are subclasses of non-convex deltahedra. shows that they may be discovered by finding the number of varying vertex's ''types''. A set of vertices is considered the same type as long as there are subgroups of the polyhedron's same group transitive on the set. Cundy shows that the great icosahedron is the only non-convex deltahedron with a single type of vertex. There are seventeen non-convex deltahedra with two types of vertex, and soon the other eleven deltahedra were later added by , Other subclasses are the isohedral deltahedron that was later discovered by both and , and the ''spiral deltahedron'' constructed by the strips of equilateral triangles was discovered by .
A ''non-convex deltahedron'' is a deltahedron that does not possess convexity, thus it has either coplanar faces or collinear edges. There are infinitely many non-convex deltahedra. Some examples are stella octangula, the third stellation of a regular icosahedron, and Boerdijk–Coxeter helix.
There are subclasses of non-convex deltahedra. shows that they may be discovered by finding the number of varying vertex's ''types''. A set of vertices is considered the same type as long as there are subgroups of the polyhedron's same group transitive on the set. Cundy shows that the great icosahedron is the only non-convex deltahedron with a single type of vertex. There are seventeen non-convex deltahedra with two types of vertex, and soon the other eleven deltahedra were later added by , Other subclasses are the isohedral deltahedron that was later discovered by both and , and the ''spiral deltahedron'' constructed by the strips of equilateral triangles was discovered by .
References
Footnotes
Works cited
* . * . * . * * . * . * . * * . * . * . * . * . * . * * * * * * . * . * . * . * . * . * .External links
* * {{MathWorld , title = Deltahedron , id = Deltahedron , mode = cs2 * Polyhedra