Decimal on:
[Wikipedia]
[Google]
[Amazon]
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting
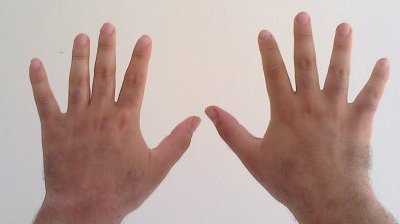 Many numeral systems of ancient civilizations use ten and its powers for representing numbers, possibly because there are ten fingers on two hands and people started counting by using their fingers. Examples are firstly the Egyptian numerals, then the
Many numeral systems of ancient civilizations use ten and its powers for representing numbers, possibly because there are ten fingers on two hands and people started counting by using their fingers. Examples are firstly the Egyptian numerals, then the
 Most modern
Most modern
 Many ancient cultures calculated with numerals based on ten, sometimes argued due to human hands typically having ten fingers/digits. Standardized weights used in the
Many ancient cultures calculated with numerals based on ten, sometimes argued due to human hands typically having ten fingers/digits. Standardized weights used in the 
 Decimal fractions were first developed and used by the Chinese in the end of 4th century BCE, and then spread to the Middle East and from there to Europe. The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional. Lam Lay Yong, "The Development of Hindu–Arabic and Traditional Chinese Arithmetic", ''Chinese Science'', 1996 p. 38, Kurt Vogel notation
Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by
:::::
::::: , meaning
:::::
:::::096644
J. Lennart Berggren notes that positional decimal fractions appear for the first time in a book by the Arab mathematician Abu'l-Hasan al-Uqlidisi written in the 10th century. The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them. The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century.
Decimal fractions were first developed and used by the Chinese in the end of 4th century BCE, and then spread to the Middle East and from there to Europe. The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional. Lam Lay Yong, "The Development of Hindu–Arabic and Traditional Chinese Arithmetic", ''Chinese Science'', 1996 p. 38, Kurt Vogel notation
Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by
:::::
::::: , meaning
:::::
:::::096644
J. Lennart Berggren notes that positional decimal fractions appear for the first time in a book by the Arab mathematician Abu'l-Hasan al-Uqlidisi written in the 10th century. The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them. The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century.
Introduction to Old Norse
p. 293, gives number names that belong to this system. An expression cognate to 'one hundred and eighty' translates to 200, and the cognate to 'two hundred' translates to 240
Goodare
details the use of the long hundred in Scotland in the Middle Ages, giving examples such as calculations where the carry implies i C (i.e. one hundred) as 120, etc. That the general population were not alarmed to encounter such numbers suggests common enough use. It is also possible to avoid hundred-like numbers by using intermediate units, such as stones and pounds, rather than a long count of pounds. Goodare gives examples of numbers like vii score, where one avoids the hundred by using extended scores. There is also a paper by W.H. Stevenson, on 'Long Hundred and its uses in England'. * Many or all of the
integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
and non-integer number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual number ...
s. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''.
A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value.
The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an integer, and is a non-negative integer.
The decimal system has been extended to ''infinite decimals'' for representing any real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
, by using an infinite sequence of digits after the decimal separator (see decimal representation). In this context, the decimal numerals with a finite number of non-zero digits after the decimal separator are sometimes called ''terminating decimals''. A ''repeating decimal
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero. It can be shown that a number is rational i ...
'' is an infinite decimal that, after some place, repeats indefinitely the same sequence of digits (e.g., ). An infinite decimal represents a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
, the quotient of two integers, if and only if it is a repeating decimal or has a finite number of non-zero digits.
Origin
 Many numeral systems of ancient civilizations use ten and its powers for representing numbers, possibly because there are ten fingers on two hands and people started counting by using their fingers. Examples are firstly the Egyptian numerals, then the
Many numeral systems of ancient civilizations use ten and its powers for representing numbers, possibly because there are ten fingers on two hands and people started counting by using their fingers. Examples are firstly the Egyptian numerals, then the Brahmi numerals
The Brahmi numerals are a numeral system attested from the 3rd century BCE (somewhat later in the case of most of the tens). They are a non positional decimal system. They are the direct graphic ancestors of the modern Hindu–Arabic numeral ...
, Greek numerals
Greek numerals, also known as Ionic, Ionian, Milesian, or Alexandrian numerals, are a system of writing numbers using the letters of the Greek alphabet. In modern Greece, they are still used for ordinal numbers and in contexts similar to those ...
, Hebrew numerals
The system of Hebrew numerals is a quasi-decimal alphabetic numeral system using the letters of the Hebrew alphabet.
The system was adapted from that of the Greek numerals in the late 2nd century BCE.
The current numeral system is also known as ...
, Roman numerals
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, ...
, and Chinese numerals. Very large numbers were difficult to represent in these old numeral systems, and only the best mathematicians were able to multiply or divide large numbers. These difficulties were completely solved with the introduction of the Hindu–Arabic numeral system for representing integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
s. This system has been extended to represent some non-integer numbers, called '' decimal fractions'' or ''decimal numbers'', for forming the ''decimal numeral system''.
Decimal notation
For writing numbers, the decimal system uses tendecimal digit
A numerical digit (often shortened to just digit) is a single symbol used alone (such as "2") or in combinations (such as "25"), to represent numbers in a positional numeral system. The name "digit" comes from the fact that the ten digits ( Lati ...
s, a decimal mark, and, for negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. A debt that is owed ma ...
s, a minus sign
The plus and minus signs, and , are mathematical symbols used to represent the notions of positive and negative, respectively. In addition, represents the operation of addition, which results in a sum, while represents subtraction, resul ...
"−". The decimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; the decimal separator is the dot "" in many countries (mostly English-speaking), and a comma "" in other countries.
For representing a non-negative number, a decimal numeral consists of
* either a (finite) sequence of digits (such as "2017"), where the entire sequence represents an integer,
*:
*or a decimal mark separating two sequences of digits (such as "20.70828")
::.
If , that is, if the first sequence contains at least two digits, it is generally assumed that the first digit is not zero. In some circumstances it may be useful to have one or more 0's on the left; this does not change the value represented by the decimal: for example, . Similarly, if the final digit on the right of the decimal mark is zero—that is, if —it may be removed; conversely, trailing zeros may be added after the decimal mark without changing the represented number; for example, and .
For representing a negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. A debt that is owed ma ...
, a minus sign is placed before .
The numeral represents the number
:.
The '' integer part'' or ''integral part'' of a decimal numeral is the integer written to the left of the decimal separator (see also truncation
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point.
Truncation and floor function
Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathb ...
). For a non-negative decimal numeral, it is the largest integer that is not greater than the decimal. The part from the decimal separator to the right is the ''fractional part
The fractional part or decimal part of a non‐negative real number x is the excess beyond that number's integer part. If the latter is defined as the largest integer not greater than , called floor of or \lfloor x\rfloor, its fractional part ca ...
'', which equals the difference between the numeral and its integer part.
When the integral part of a numeral is zero, it may occur, typically in computing
Computing is any goal-oriented activity requiring, benefiting from, or creating computing machinery. It includes the study and experimentation of algorithmic processes, and development of both hardware and software. Computing has scientific, ...
, that the integer part is not written (for example, , instead of ). In normal writing, this is generally avoided, because of the risk of confusion between the decimal mark and other punctuation.
In brief, the contribution of each digit to the value of a number depends on its position in the numeral. That is, the decimal system is a positional numeral system.
Decimal fractions
Decimal fractions (sometimes called decimal numbers, especially in contexts involving explicit fractions) are therational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
s that may be expressed as a fraction
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
whose denominator is a power of ten. For example, the decimals represent the fractions , , , and , and are therefore decimal numbers.
More generally, a decimal with digits after the separator (a point or comma) represents the fraction with denominator , whose numerator is the integer obtained by removing the separator.
It follows that a number is a decimal fraction if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is bic ...
it has a finite decimal representation.
Expressed as a fully reduced fraction, the decimal numbers are those whose denominator is a product of a power of 2 and a power of 5. Thus the smallest denominators of decimal numbers are
:
Real number approximation
Decimal numerals do not allow an exact representation for allreal number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, e.g. for the real number . Nevertheless, they allow approximating every real number with any desired accuracy, e.g., the decimal 3.14159 approximates the real , being less than 10−5 off; so decimals are widely used in science
Science is a systematic endeavor that builds and organizes knowledge in the form of testable explanations and predictions about the universe.
Science may be as old as the human species, and some of the earliest archeological evidence ...
, engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more speciali ...
and everyday life.
More precisely, for every real number and every positive integer , there are two decimals and with at most ' digits after the decimal mark such that and .
Numbers are very often obtained as the result of measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared ...
. As measurements are subject to measurement uncertainty
In metrology, measurement uncertainty is the expression of the statistical dispersion of the values attributed to a measured quantity. All measurements are subject to uncertainty and a measurement result is complete only when it is accompanied by ...
with a known upper bound, the result of a measurement is well-represented by a decimal with digits after the decimal mark, as soon as the absolute measurement error is bounded from above by . In practice, measurement results are often given with a certain number of digits after the decimal point, which indicate the error bounds. For example, although 0.080 and 0.08 denote the same number, the decimal numeral 0.080 suggests a measurement with an error less than 0.001, while the numeral 0.08 indicates an absolute error bounded by 0.01. In both cases, the true value of the measured quantity could be, for example, 0.0803 or 0.0796 (see also significant figures).
Infinite decimal expansion
For areal number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
and an integer , let denote the (finite) decimal expansion of the greatest number that is not greater than ' that has exactly digits after the decimal mark. Let denote the last digit of . It is straightforward to see that may be obtained by appending to the right of . This way one has
:,
and the difference of and amounts to
:,
which is either 0, if , or gets arbitrarily small as ' tends to infinity. According to the definition of a limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
, ' is the limit of when ' tends to infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions am ...
. This is written asor
: ,
which is called an infinite decimal expansion of '.
Conversely, for any integer and any sequence of digits the (infinite) expression is an ''infinite decimal expansion'' of a real number '. This expansion is unique if neither all are equal to 9 nor all are equal to 0 for ' large enough (for all ' greater than some natural number ).
If all for equal to 9 and , the limit of the sequence is the decimal fraction obtained by replacing the last digit that is not a 9, i.e.: , by , and replacing all subsequent 9s by 0s (see 0.999...).
Any such decimal fraction, i.e.: for , may be converted to its equivalent infinite decimal expansion by replacing by and replacing all subsequent 0s by 9s (see 0.999...).
In summary, every real number that is not a decimal fraction has a unique infinite decimal expansion. Each decimal fraction has exactly two infinite decimal expansions, one containing only 0s after some place, which is obtained by the above definition of , and the other containing only 9s after some place, which is obtained by defining as the greatest number that is ''less'' than , having exactly ' digits after the decimal mark.
Rational numbers
Long division allows computing the infinite decimal expansion of arational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ra ...
. If the rational number is a decimal fraction, the division stops eventually, producing a decimal numeral, which may be prolongated into an infinite expansion by adding infinitely many zeros. If the rational number is not a decimal fraction, the division may continue indefinitely. However, as all successive remainders are less than the divisor, there are only a finite number of possible remainders, and after some place, the same sequence of digits must be repeated indefinitely in the quotient. That is, one has a ''repeating decimal''. For example,
: = 0.012345679012... (with the group 012345679 indefinitely repeating).
The converse is also true: if, at some point in the decimal representation of a number, the same string of digits starts repeating indefinitely, the number is rational.
or, dividing both numerator and denominator by 6, .
Decimal computation
computer
A computer is a machine that can be programmed to carry out sequences of arithmetic or logical operations ( computation) automatically. Modern digital electronic computers can perform generic sets of operations known as programs. These prog ...
hardware and software systems commonly use a binary representation internally (although many early computers, such as the ENIAC or the IBM 650
The IBM 650 Magnetic Drum Data-Processing Machine is an early digital computer produced by IBM in the mid-1950s. It was the first mass produced computer in the world. Almost 2,000 systems were produced, the last in 1962, and it was the fir ...
, used decimal representation internally).
For external use by computer specialists, this binary representation is sometimes presented in the related octal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, ...
or hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, he ...
systems.
For most purposes, however, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; computer programs express literals in decimal by default. (123.1, for example, is written as such in a computer program, even though many computer languages are unable to encode that number precisely.)
Both computer hardware and software also use internal representations which are effectively decimal for storing decimal values and doing arithmetic. Often this arithmetic is done on data which are encoded using some variant of binary-coded decimal
In computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used ...
, especially in database implementations, but there are other decimal representations in use (including decimal floating point such as in newer revisions of the IEEE 754 Standard for Floating-Point Arithmetic).
Decimal arithmetic is used in computers so that decimal fractional results of adding (or subtracting) values with a fixed length of their fractional part always are computed to this same length of precision. This is especially important for financial calculations, e.g., requiring in their results integer multiples of the smallest currency unit for book keeping purposes. This is not possible in binary, because the negative powers of have no finite binary fractional representation; and is generally impossible for multiplication (or division). See Arbitrary-precision arithmetic for exact calculations.
History
 Many ancient cultures calculated with numerals based on ten, sometimes argued due to human hands typically having ten fingers/digits. Standardized weights used in the
Many ancient cultures calculated with numerals based on ten, sometimes argued due to human hands typically having ten fingers/digits. Standardized weights used in the Indus Valley civilization
The Indus Valley Civilisation (IVC), also known as the Indus Civilisation was a Bronze Age civilisation in the northwestern regions of South Asia, lasting from 3300 BCE to 1300 BCE, and in its mature form 2600 BCE to 1900& ...
() were based on the ratios: 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200, and 500, while their standardized ruler – the ''Mohenjo-daro ruler'' – was divided into ten equal parts. Egyptian hieroglyphs
Egyptian hieroglyphs (, ) were the formal writing system used in Ancient Egypt, used for writing the Egyptian language. Hieroglyphs combined logographic, syllabic and alphabetic elements, with some 1,000 distinct characters.There were about 1, ...
, in evidence since around 3000 BCE, used a purely decimal system, as did the Cretan hieroglyphs () of the Minoans whose numerals are closely based on the Egyptian model. The decimal system was handed down to the consecutive Bronze Age cultures of Greece, including Linear A (c. 18th century BCE−1450 BCE) and Linear B
Linear B was a syllabic script used for writing in Mycenaean Greek, the earliest attested form of Greek. The script predates the Greek alphabet by several centuries. The oldest Mycenaean writing dates to about 1400 BC. It is descended from ...
(c. 1375−1200 BCE) – the number system of classical Greece
Classical Greece was a period of around 200 years (the 5th and 4th centuries BC) in Ancient Greece,The "Classical Age" is "the modern designation of the period from about 500 B.C. to the death of Alexander the Great in 323 B.C." ( Thomas R. Marti ...
also used powers of ten, including, Roman numerals
Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written with combinations of letters from the Latin alphabet, ...
, an intermediate base of 5. Notably, the polymath Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientis ...
(c. 287–212 BCE) invented a decimal positional system in his Sand Reckoner
''The Sand Reckoner'' ( el, Ψαμμίτης, ''Psammites'') is a work by Archimedes, an Ancient Greek mathematician of the 3rd century BC, in which he set out to determine an upper bound for the number of grains of sand that fit into the unive ...
which was based on 108 and later led the German mathematician Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refer ...
to lament what heights science would have already reached in his days if Archimedes had fully realized the potential of his ingenious discovery. Hittite hieroglyphs (since 15th century BCE) were also strictly decimal.
Some non-mathematical ancient texts such as the Vedas
upright=1.2, The Vedas are ancient Sanskrit texts of Hinduism. Above: A page from the '' Atharvaveda''.
The Vedas (, , ) are a large body of religious texts originating in ancient India. Composed in Vedic Sanskrit, the texts constitute th ...
, dating back to 1700–900 BCE make use of decimals and mathematical decimal fractions.
The Egyptian hieratic numerals, the Greek alphabet numerals, the Hebrew alphabet numerals, the Roman numerals, the Chinese numerals and early Indian Brahmi numerals are all non-positional decimal systems, and required large numbers of symbols. For instance, Egyptian numerals used different symbols for 10, 20 to 90, 100, 200 to 900, 1000, 2000, 3000, 4000, to 10,000.
The world's earliest positional decimal system was the Chinese rod calculus.
History of decimal fractions
 Decimal fractions were first developed and used by the Chinese in the end of 4th century BCE, and then spread to the Middle East and from there to Europe. The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional. Lam Lay Yong, "The Development of Hindu–Arabic and Traditional Chinese Arithmetic", ''Chinese Science'', 1996 p. 38, Kurt Vogel notation
Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by
:::::
::::: , meaning
:::::
:::::096644
J. Lennart Berggren notes that positional decimal fractions appear for the first time in a book by the Arab mathematician Abu'l-Hasan al-Uqlidisi written in the 10th century. The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them. The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century.
Decimal fractions were first developed and used by the Chinese in the end of 4th century BCE, and then spread to the Middle East and from there to Europe. The written Chinese decimal fractions were non-positional. However, counting rod fractions were positional. Lam Lay Yong, "The Development of Hindu–Arabic and Traditional Chinese Arithmetic", ''Chinese Science'', 1996 p. 38, Kurt Vogel notation
Qin Jiushao in his book Mathematical Treatise in Nine Sections (1247) denoted 0.96644 by
:::::
::::: , meaning
:::::
:::::096644
J. Lennart Berggren notes that positional decimal fractions appear for the first time in a book by the Arab mathematician Abu'l-Hasan al-Uqlidisi written in the 10th century. The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to represent them. The Persian mathematician Jamshīd al-Kāshī claimed to have discovered decimal fractions himself in the 15th century. Al Khwarizmi
Muḥammad ibn Mūsā al-Khwārizmī ( ar, محمد بن موسى الخوارزمي, Muḥammad ibn Musā al-Khwārazmi; ), or al-Khwarizmi, was a Persian polymath from Khwarazm, who produced vastly influential works in mathematics, astronom ...
introduced fraction to Islamic countries in the early 9th century; a Chinese author has alleged that his fraction presentation was an exact copy of traditional Chinese mathematical fraction from Sunzi Suanjing. This form of fraction with numerator on top and denominator at bottom without a horizontal bar was also used by al-Uqlidisi and by al-Kāshī in his work "Arithmetic Key".
A forerunner of modern European decimal notation was introduced by Simon Stevin in the 16th century.
John Napier introduced using the period (.) to separate the integer part of a decimal number from the fractional part in his book on constructing tables of logarithms, published posthumously in 1620.
Natural languages
A method of expressing every possiblenatural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
using a set of ten symbols emerged in India. Several Indian languages show a straightforward decimal system. Many Indo-Aryan and Dravidian languages
The Dravidian languages (or sometimes Dravidic) are a family of languages spoken by 250 million people, mainly in southern India, north-east Sri Lanka, and south-west Pakistan. Since the colonial era, there have been small but significant im ...
have numbers between 10 and 20 expressed in a regular pattern of addition to 10.
The Hungarian language
Hungarian () is an Uralic language spoken in Hungary and parts of several neighbouring countries. It is the official language of Hungary and one of the 24 official languages of the European Union. Outside Hungary, it is also spoken by Hungar ...
also uses a straightforward decimal system. All numbers between 10 and 20 are formed regularly (e.g. 11 is expressed as "tizenegy" literally "one on ten"), as with those between 20 and 100 (23 as "huszonhárom" = "three on twenty").
A straightforward decimal rank system with a word for each order (10 , 100 , 1000 , 10,000 ), and in which 11 is expressed as ''ten-one'' and 23 as ''two-ten-three'', and 89,345 is expressed as 8 (ten thousands) 9 (thousand) 3 (hundred) 4 (tens) 5 is found in Chinese, and in Vietnamese with a few irregularities. Japanese, Korean, and Thai have imported the Chinese decimal system. Many other languages with a decimal system have special words for the numbers between 10 and 20, and decades. For example, in English 11 is "eleven" not "ten-one" or "one-teen".
Incan languages such as Quechua and Aymara have an almost straightforward decimal system, in which 11 is expressed as ''ten with one'' and 23 as ''two-ten with three''.
Some psychologists suggest irregularities of the English names of numerals may hinder children's counting ability.
Other bases
Some cultures do, or did, use other bases of numbers. *Pre-Columbian
In the history of the Americas, the pre-Columbian era spans from the original settlement of North and South America in the Upper Paleolithic period through European colonization, which began with Christopher Columbus's voyage of 1492. Usually, ...
Mesoamerica
Mesoamerica is a historical region and cultural area in southern North America and most of Central America. It extends from approximately central Mexico through Belize, Guatemala, El Salvador, Honduras, Nicaragua, and northern Costa Rica. Wit ...
n cultures such as the Maya used a base-20 system (perhaps based on using all twenty fingers and toes).
* The Yuki language in California
California is a state in the Western United States, located along the Pacific Coast. With nearly 39.2million residents across a total area of approximately , it is the most populous U.S. state and the 3rd largest by area. It is also the m ...
and the Pamean languages in Mexico
Mexico (Spanish language, Spanish: México), officially the United Mexican States, is a List of sovereign states, country in the southern portion of North America. It is borders of Mexico, bordered to the north by the United States; to the so ...
have octal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, ...
( base-8) systems because the speakers count using the spaces between their fingers rather than the fingers themselves.
* The existence of a non-decimal base in the earliest traces of the Germanic languages is attested by the presence of words and glosses meaning that the count is in decimal (cognates to "ten-count" or "tenty-wise"); such would be expected if normal counting is not decimal, and unusual if it were. Where this counting system is known, it is based on the "long hundred" = 120, and a "long thousand" of 1200. The descriptions like "long" only appear after the "small hundred" of 100 appeared with the Christians. Gordon'Introduction to Old Norse
p. 293, gives number names that belong to this system. An expression cognate to 'one hundred and eighty' translates to 200, and the cognate to 'two hundred' translates to 240
Goodare
details the use of the long hundred in Scotland in the Middle Ages, giving examples such as calculations where the carry implies i C (i.e. one hundred) as 120, etc. That the general population were not alarmed to encounter such numbers suggests common enough use. It is also possible to avoid hundred-like numbers by using intermediate units, such as stones and pounds, rather than a long count of pounds. Goodare gives examples of numbers like vii score, where one avoids the hundred by using extended scores. There is also a paper by W.H. Stevenson, on 'Long Hundred and its uses in England'. * Many or all of the
Chumashan languages
Chumashan was a family of languages that were spoken on the southern California coast by Native American Chumash people, from the Coastal plains and valleys of San Luis Obispo to Malibu, neighboring inland and Transverse Ranges valleys and c ...
originally used a base-4 counting system, in which the names for numbers were structured according to multiples of 4 and 16.
* Many languages use quinary (base-5) number systems, including Gumatj, Nunggubuyu, Kuurn Kopan Noot and Saraveca. Of these, Gumatj is the only true 5–25 language known, in which 25 is the higher group of 5.
* Some Nigeria
Nigeria ( ), , ig, Naìjíríyà, yo, Nàìjíríà, pcm, Naijá , ff, Naajeeriya, kcg, Naijeriya officially the Federal Republic of Nigeria, is a country in West Africa. It is situated between the Sahel to the north and the Gulf o ...
ns use duodecimal
The duodecimal system (also known as base 12, dozenal, or, rarely, uncial) is a positional notation numeral system using twelve as its base. The number twelve (that is, the number written as "12" in the decimal numerical system) is instead wr ...
systems. So did some small communities in India and Nepal, as indicated by their languages.
* The Huli language of Papua New Guinea
Papua New Guinea (abbreviated PNG; , ; tpi, Papua Niugini; ho, Papua Niu Gini), officially the Independent State of Papua New Guinea ( tpi, Independen Stet bilong Papua Niugini; ho, Independen Stet bilong Papua Niu Gini), is a country i ...
is reported to have base-15 numbers. ''Ngui'' means 15, ''ngui ki'' means 15 × 2 = 30, and ''ngui ngui'' means 15 × 15 = 225.
* Umbu-Ungu
Kaugel (Gawigl) is one of the languages spoken in the Southern Highlands province of Papua New Guinea. Native speakers call the area on the Southern Highlands side of the Kaugel River from the Western Highlands province home.
Dialects are Aua ...
, also known as Kakoli, is reported to have base-24
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the ...
numbers. ''Tokapu'' means 24, ''tokapu talu'' means 24 × 2 = 48, and ''tokapu tokapu'' means 24 × 24 = 576.
* Ngiti is reported to have a base-32 number system with base-4 cycles.
* The Ndom language
Ndom is a language spoken on Yos Sudarso Island in Papua province, Indonesia. It is reported to have numbers in senary
A senary () numeral system (also known as base-6, heximal, or seximal) has six as its base. It has been adopted independ ...
of Papua New Guinea
Papua New Guinea (abbreviated PNG; , ; tpi, Papua Niugini; ho, Papua Niu Gini), officially the Independent State of Papua New Guinea ( tpi, Independen Stet bilong Papua Niugini; ho, Independen Stet bilong Papua Niu Gini), is a country i ...
is reported to have base-6 numerals. ''Mer'' means 6, ''mer an thef'' means 6 × 2 = 12, ''nif'' means 36, and ''nif thef'' means 36×2 = 72.
See also
Notes
References
{{Authority control Elementary arithmetic Fractions (mathematics) Positional numeral systems