Cutting-plane method on:
[Wikipedia]
[Google]
[Amazon]
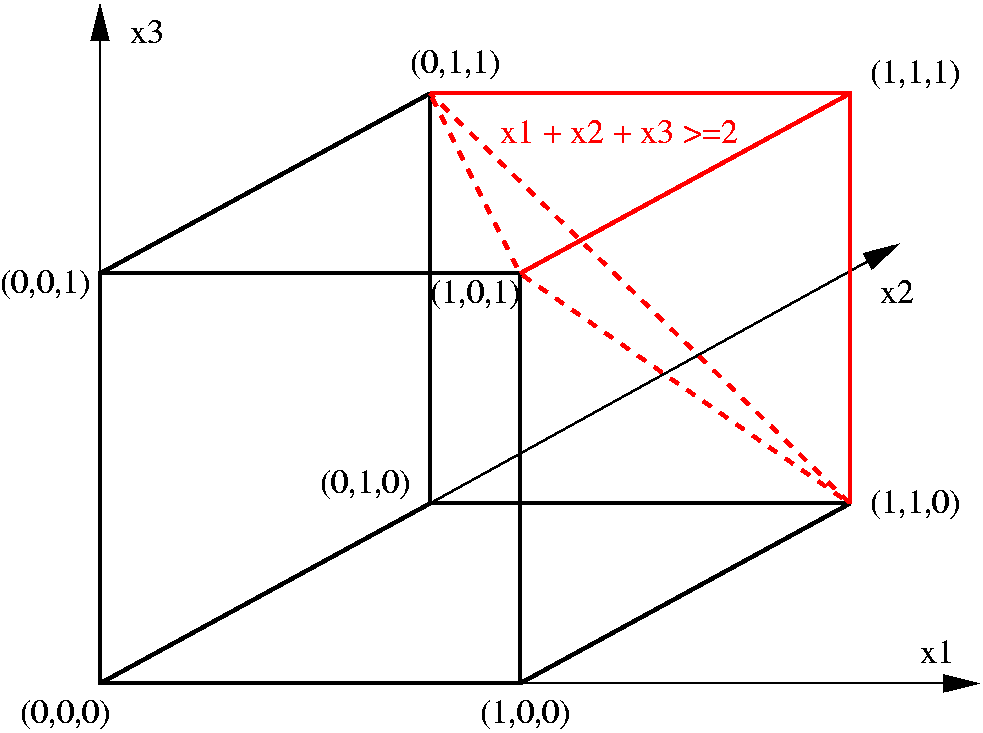 In
In
* Cornuéjols, Gérard (2007). Revival of the Gomory Cuts in the 1990s. ''Annals of Operations Research'', Vol. 149 (2007), pp. 63–66.
"Integer Programming" Section 9.8
''Applied Mathematical Programming'' Chapter 9 Integer Programming (full text). Bradley, Hax, and Magnanti (Addison-Wesley, 1977) {{Optimization algorithms, convex Optimization algorithms and methods
 In
In mathematical
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
, the cutting-plane method is any of a variety of optimization methods that iteratively refine a feasible set or objective function by means of linear inequalities, termed ''cuts''. Such procedures are commonly used to find integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the languag ...
solutions to mixed integer linear programming (MILP) problems, as well as to solve general, not necessarily differentiable convex optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization pr ...
problems. The use of cutting planes to solve MILP was introduced by Ralph E. Gomory.
Cutting plane methods for MILP work by solving a non-integer linear program, the linear relaxation of the given integer program. The theory of Linear Programming dictates that under mild assumptions (if the linear program has an optimal solution, and if the feasible region does not contain a line), one can always find an extreme point or a corner point that is optimal. The obtained optimum
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfi ...
is tested for being an integer solution. If it is not, there is guaranteed to exist a linear inequality that ''separates'' the optimum from the convex hull of the true feasible set. Finding such an inequality is the ''separation problem'', and such an inequality is a ''cut''. A cut can be added to the relaxed linear program. Then, the current non-integer solution is no longer feasible to the relaxation. This process is repeated until an optimal integer solution is found.
Cutting-plane methods for general convex continuous optimization and variants are known under various names: Kelley's method, Kelley–Cheney–Goldstein method, and bundle methods. They are popularly used for non-differentiable convex minimization, where a convex objective function and its subgradient can be evaluated efficiently but usual gradient methods for differentiable optimization can not be used. This situation is most typical for the concave maximization of Lagrangian dual functions. Another common situation is the application of the Dantzig–Wolfe decomposition
Dantzig–Wolfe decomposition is an algorithm for solving linear programming problems with special structure. It was originally developed by George Dantzig and Philip Wolfe and initially published in 1960. Many texts on linear programming have s ...
to a structured optimization problem in which formulations with an exponential number of variables are obtained. Generating these variables on demand by means of delayed column generation
Column generation or delayed column generation is an efficient algorithm for solving large linear programs.
The overarching idea is that many linear programs are too large to consider all the variables explicitly. The idea is thus to start by sol ...
is identical to performing a cutting plane on the respective dual problem.
Gomory's cut
Cutting planes were proposed byRalph Gomory
Ralph Edward Gomory (born May 7, 1929) is an American applied mathematician and executive. Gomory worked at IBM as a researcher and later as an executive. During that time, his research led to the creation of new areas of applied mathematics.
...
in the 1950s as a method for solving integer programming and mixed-integer programming problems. However, most experts, including Gomory himself, considered them to be impractical due to numerical instability, as well as ineffective because many rounds of cuts were needed to make progress towards the solution. Things turned around when in the mid-1990s Gérard Cornuéjols and co-workers showed them to be very effective in combination with branch-and-bound
Branch and bound (BB, B&B, or BnB) is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate soluti ...
(called branch-and-cut) and ways to overcome numerical instabilities. Nowadays, all commercial MILP solvers use Gomory cuts in one way or another. Gomory cuts are very efficiently generated from a simplex tableau, whereas many other types of cuts are either expensive or even NP-hard to separate. Among other general cuts for MILP, most notably lift-and-project dominates Gomory cuts.
Let an integer programming problem be formulated (in canonical form
In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides the simplest representation of an ...
) as:
:
The method proceeds by first dropping the requirement that the xi be integers and solving the associated linear programming problem to obtain a basic feasible solution. Geometrically, this solution will be a vertex of the convex polytope consisting of all feasible points. If this vertex is not an integer point then the method finds a hyperplane with the vertex on one side and all feasible integer points on the other. This is then added as an additional linear constraint to exclude the vertex found, creating a modified linear program. The new program is then solved and the process is repeated until an integer solution is found.
Using the simplex method
In mathematical optimization, Dantzig's simplex algorithm (or simplex method) is a popular algorithm for linear programming.
The name of the algorithm is derived from the concept of a simplex and was suggested by T. S. Motzkin. Simplices are n ...
to solve a linear program produces a set of equations of the form
:
where ''xi'' is a basic variable and the ''xjs are the nonbasic variables. Rewrite this equation so that the integer parts are on the left side and the fractional parts are on the right side:
:
For any integer point in the feasible region, the right side of this equation is less than 1 and the left side is an integer, therefore the common value must be less than or equal to 0. So the inequality
:
must hold for any integer point in the feasible region. Furthermore, nonbasic variables are equal to 0s in any basic solution and if ''xi'' is not an integer for the basic solution ''x'',
:
So the inequality above excludes the basic feasible solution and thus is a cut with the desired properties. Introducing a new slack variable xk for this inequality, a new constraint is added to the linear program, namely
:
Convex optimization
Cutting plane methods are also applicable in nonlinear programming. The underlying principle is to approximate thefeasible region
In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points (sets of values of the choice variables) of an optimization problem that satisfy the problem's constraints, potent ...
of a nonlinear (convex) program by a finite set of closed half spaces and to solve a sequence of approximating linear programs.
See also
*Benders' decomposition
Benders decomposition (or Benders' decomposition) is a technique in mathematical programming that allows the solution of very large linear programming problems that have a special block structure. This block structure often occurs in applications ...
* Branch and cut
*Branch and bound
Branch and bound (BB, B&B, or BnB) is an algorithm design paradigm for discrete and combinatorial optimization problems, as well as mathematical optimization. A branch-and-bound algorithm consists of a systematic enumeration of candidate solut ...
* Column generation
*Dantzig–Wolfe decomposition
Dantzig–Wolfe decomposition is an algorithm for solving linear programming problems with special structure. It was originally developed by George Dantzig and Philip Wolfe and initially published in 1960. Many texts on linear programming have s ...
References
* * Avriel, Mordecai (2003). ''Nonlinear Programming: Analysis and Methods.'' Dover Publications. * Cornuéjols, Gérard (2008). Valid Inequalities for Mixed Integer Linear Programs. ''Mathematical Programming Ser. B'', (2008) 112:3–44.* Cornuéjols, Gérard (2007). Revival of the Gomory Cuts in the 1990s. ''Annals of Operations Research'', Vol. 149 (2007), pp. 63–66.
External links
"Integer Programming" Section 9.8
''Applied Mathematical Programming'' Chapter 9 Integer Programming (full text). Bradley, Hax, and Magnanti (Addison-Wesley, 1977) {{Optimization algorithms, convex Optimization algorithms and methods