Branching process on:
[Wikipedia]
[Google]
[Amazon]
In
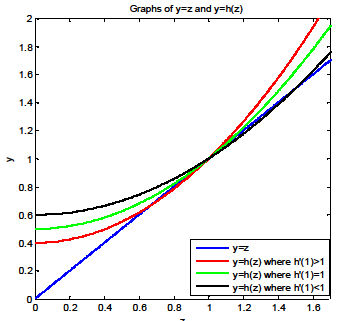 Case 1 has another intersect point at ''z'' < 1 (see the red curve in the graph).
Case 2 has only one intersect point at ''z'' = 1.(See the green curve in the graph)
Case 3 has another intersect point at ''z'' > 1.(See the black curve in the graph)
In case 1, the ultimate extinction probability is strictly less than one. For case 2 and 3, the ultimate extinction probability equals to one.
By observing that ''h′''(1) = ''p''1 + 2''p''2 + 3''p''3 + ... = ''μ'' is exactly the expected number of offspring a parent could produce, it can be concluded that for a branching process with generating function ''h''(''z'') for the number of offspring of a given parent, if the mean number of offspring produced by a single parent is less than or equal to one, then the ultimate extinction probability is one. If the mean number of offspring produced by a single parent is greater than one, then the ultimate extinction probability is strictly less than one.
Case 1 has another intersect point at ''z'' < 1 (see the red curve in the graph).
Case 2 has only one intersect point at ''z'' = 1.(See the green curve in the graph)
Case 3 has another intersect point at ''z'' > 1.(See the black curve in the graph)
In case 1, the ultimate extinction probability is strictly less than one. For case 2 and 3, the ultimate extinction probability equals to one.
By observing that ''h′''(1) = ''p''1 + 2''p''2 + 3''p''3 + ... = ''μ'' is exactly the expected number of offspring a parent could produce, it can be concluded that for a branching process with generating function ''h''(''z'') for the number of offspring of a given parent, if the mean number of offspring produced by a single parent is less than or equal to one, then the ultimate extinction probability is one. If the mean number of offspring produced by a single parent is greater than one, then the ultimate extinction probability is strictly less than one.
Introduction to Probability
, 2nd ed. Section 10.3 discusses branching processes in detail together with the application of generating functions to study them. * G. R. Grimmett and D. R. Stirzaker, ''Probability and Random Processes'', 2nd ed., Clarendon Press, Oxford, 1992. Section 5.4 discusses the model of branching processes described above. Section 5.5 discusses a more general model of branching processes known as age-dependent branching processes, in which individuals live for more than one generation. {{DEFAULTSORT:Branching Process Markov processes
probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
, a branching process is a type of mathematical object known as a stochastic process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Sto ...
, which consists of collections of random variables
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. The term 'random variable' in its mathematical definition refers ...
indexed by some set, usually natural or non-negative real numbers. The original purpose of branching processes was to serve as a mathematical model of a population in which each individual in generation produces some random number of individuals in generation , according, in the simplest case, to a fixed probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surname
In many societies, a surname, family name, or last name is the mostly hereditary portion of one's personal name that indicates one's family. It is typically combined with a given name to form the full name of a person, although several give ...
s in genealogy
Genealogy () is the study of families, family history, and the tracing of their lineages. Genealogists use oral interviews, historical records, genetic analysis, and other records to obtain information about a family and to demonstrate kin ...
or the propagation of neutrons in a nuclear reactor
A nuclear reactor is a device used to initiate and control a Nuclear fission, fission nuclear chain reaction. They are used for Nuclear power, commercial electricity, nuclear marine propulsion, marine propulsion, Weapons-grade plutonium, weapons ...
.
A central question in the theory of branching processes is the probability of ultimate extinction, where no individuals exist after some finite number of generations. Using Wald's equation, it can be shown that starting with one individual in generation zero, the expected size of generation ''n'' equals ''μ''''n'' where ''μ'' is the expected number of children of each individual. If ''μ'' < 1, then the expected number of individuals goes rapidly to zero, which implies ultimate extinction with probability 1 by Markov's inequality
In probability theory, Markov's inequality gives an upper bound on the probability that a non-negative random variable is greater than or equal to some positive Constant (mathematics), constant. Markov's inequality is tight in the sense that for e ...
. Alternatively, if ''μ'' > 1, then the probability of ultimate extinction is less than 1 (but not necessarily zero; consider a process where each individual either has 0 or 100 children with equal probability. In that case, ''μ'' = 50, but probability of ultimate extinction is greater than 0.5, since that's the probability that the first individual has 0 children). If ''μ'' = 1, then ultimate extinction occurs with probability 1 unless each individual always has exactly one child.
In theoretical ecology
Theoretical ecology is the scientific discipline devoted to the study of ecosystem, ecological systems using theoretical methods such as simple conceptual models, mathematical models, computer simulation, computational simulations, and advanced d ...
, the parameter ''μ'' of a branching process is called the basic reproductive rate.
Mathematical formulation
The most common formulation of a branching process is that of theGalton–Watson process
The Galton–Watson process, also called the Bienaymé-Galton-Watson process or the Galton-Watson branching process, is a branching stochastic process arising from Francis Galton's statistical investigation of the extinction of family names. The ...
. Let ''Z''''n'' denote the state in period ''n'' (often interpreted as the size of generation ''n''), and let ''X''''n,i'' be a random variable denoting the number of direct successors of member ''i'' in period ''n'', where ''X''''n,i'' are independent and identically distributed random variables over all ''n'' ∈ and ''i'' ∈ . Then the recurrence equation is
:
with ''Z''0 = 1.
Alternatively, the branching process can be formulated as a random walk
In mathematics, a random walk, sometimes known as a drunkard's walk, is a stochastic process that describes a path that consists of a succession of random steps on some Space (mathematics), mathematical space.
An elementary example of a rand ...
. Let ''S''''i'' denote the state in period ''i'', and let ''X''''i'' be a random variable that is iid over all ''i''. Then the recurrence equation is
:
with ''S''0 = 1. To gain some intuition for this formulation, imagine a walk where the goal is to visit every node, but every time a previously unvisited node is visited, additional nodes are revealed that must also be visited. Let ''S''''i'' represent the number of revealed but unvisited nodes in period ''i'', and let ''X''''i'' represent the number of new nodes that are revealed when node ''i'' is visited. Then in each period, the number of revealed but unvisited nodes equals the number of such nodes in the previous period, plus the new nodes that are revealed when visiting a node, minus the node that is visited. The process ends once all revealed nodes have been visited.
Continuous-time branching processes
For discrete-time branching processes, the "branching time" is fixed to be ''1'' for all individuals. For continuous-time branching processes, each individual waits for a random time (which is a continuous random variable), and then divides according to the given distribution. The waiting time for different individuals are independent, and are independent with the number of children. In general, the waiting time is an exponential variable with parameter ''λ'' for all individuals, so that the process is Markovian.Extinction problem for a Branching process
The ultimate extinction probability is given by : For any nontrivial cases (trivial cases are ones in which the probability of having no offspring is zero for every member of the population - in such cases the probability of ultimate extinction is 0), the probability of ultimate extinction equals one if ''μ'' ≤ 1 and strictly less than one if ''μ'' > 1. The process can be analyzed using the method ofprobability generating function
In probability theory, the probability generating function of a discrete random variable is a power series representation (the generating function) of the probability mass function of the random variable. Probability generating functions are of ...
. Let ''p''0, ''p''1, ''p''2, ... be the probabilities of producing 0, 1, 2, ... offspring by each individual in each generation. Let ''d''''m'' be the extinction probability by the ''m''th generation, starting with a single individual (i.e. ). Obviously, ''d''0 = 0 and ''d''1 = ''p''0. Since the probabilities for all paths that lead to 0 by the ''m''th generation must be added up, the extinction probability is nondecreasing in generations. That is,
:
Therefore, ''d''''m'' converges to a limit ''d'', and ''d'' is the ultimate extinction probability. If there are ''j'' offspring in the first generation, then to die out by the mth generation, each of these lines must die out in ''m'' − 1 generations. Since they proceed independently, the probability is (''d''''m''−1) ''j''. Thus,
:
The right-hand side of the equation is a probability generating function. Let ''h''(''z'') be the ordinary generating function for ''p''''i'':
:
Using the generating function, the previous equation becomes
:
Since ''d''''m'' → ''d'', ''d'' can be found by solving
:
This is also equivalent to finding the intersection point(s) of lines ''y'' = ''z'' and ''y'' = ''h''(''z'') for ''z'' ≥ 0. ''y'' = ''z'' is a straight line. ''y'' = ''h''(''z'') is an increasing (since ) and convex (since ) function. There are at most two intersection points. Since (1,1) is always an intersect point for the two functions, there only exist three cases: Case 1 has another intersect point at ''z'' < 1 (see the red curve in the graph).
Case 2 has only one intersect point at ''z'' = 1.(See the green curve in the graph)
Case 3 has another intersect point at ''z'' > 1.(See the black curve in the graph)
In case 1, the ultimate extinction probability is strictly less than one. For case 2 and 3, the ultimate extinction probability equals to one.
By observing that ''h′''(1) = ''p''1 + 2''p''2 + 3''p''3 + ... = ''μ'' is exactly the expected number of offspring a parent could produce, it can be concluded that for a branching process with generating function ''h''(''z'') for the number of offspring of a given parent, if the mean number of offspring produced by a single parent is less than or equal to one, then the ultimate extinction probability is one. If the mean number of offspring produced by a single parent is greater than one, then the ultimate extinction probability is strictly less than one.
Case 1 has another intersect point at ''z'' < 1 (see the red curve in the graph).
Case 2 has only one intersect point at ''z'' = 1.(See the green curve in the graph)
Case 3 has another intersect point at ''z'' > 1.(See the black curve in the graph)
In case 1, the ultimate extinction probability is strictly less than one. For case 2 and 3, the ultimate extinction probability equals to one.
By observing that ''h′''(1) = ''p''1 + 2''p''2 + 3''p''3 + ... = ''μ'' is exactly the expected number of offspring a parent could produce, it can be concluded that for a branching process with generating function ''h''(''z'') for the number of offspring of a given parent, if the mean number of offspring produced by a single parent is less than or equal to one, then the ultimate extinction probability is one. If the mean number of offspring produced by a single parent is greater than one, then the ultimate extinction probability is strictly less than one.
Size dependent branching processes
Along with discussion of a more general model of branching processes known as age-dependent branching processes by Grimmett, in which individuals live for more than one generation, Krishna Athreya has identified three distinctions between size-dependent branching processes which have general application. Athreya identifies the three classes of size-dependent branching processes as sub-critical, stable, and super-critical branching measures. For Athreya, the central parameters are crucial to control if sub-critical and super-critical unstable branching is to be avoided. Size dependent branching processes are also discussed under the topic of resource-dependent branching processExample of extinction problem
Consider a parent can produce at most two offspring. The extinction probability in each generation is: : with ''d''0 = 0. For the ultimate extinction probability, we need to find ''d'' which satisfies ''d'' = ''p''0 + ''p''1d + ''p''2''d''2. Taking as example probabilities for the numbers of offspring produced ''p''0 = 0.1, ''p''1 = 0.6, and ''p''2 = 0.3, the extinction probability for the first 20 generations is as follows: In this example, we can solve algebraically that ''d'' = 1/3, and this is the value to which the extinction probability converges with increasing generations.Simulating branching processes
Branching processes can be simulated for a range of problems. One specific use of simulated branching process is in the field of evolutionary biology. Phylogenetic trees, for example, can be simulated under several models, helping to develop and validate estimation methods as well as supporting hypothesis testing.Multitype branching processes
In multitype branching processes, individuals are not identical, but can be classified into ''n'' types. After each time step, an individual of type ''i'' will produce individuals of different types, and , a random vector representing the numbers of children in different types, satisfies a probability distribution on . For example, consider the population of cancer stem cells (CSCs) and non-stem cancer cells (NSCCs). After each time interval, each CSC has probability to produce two CSCs (symmetric division), probability to produce one CSC and one NSCC (asymmetric division), probability to produce one CSC (stagnation), and probability to produce nothing (death); each NSCC has probability to produce two NSCCs (symmetric division), probability to produce one NSCC (stagnation), and probability to produce nothing (death).Law of large numbers for multitype branching processes
For multitype branching processes that the populations of different types grow exponentially, the proportions of different types converge almost surely to a constant vector under some mild conditions. This is the strong law of large numbers for multitype branching processes. For continuous-time cases, proportions of the population expectation satisfy anODE
An ode (from ) is a type of lyric poetry, with its origins in Ancient Greece. Odes are elaborately structured poems praising or glorifying an event or individual, describing nature intellectually as well as emotionally. A classic ode is structu ...
system, which has a unique attracting fixed point. This fixed point is just the vector that the proportions converge to in the law of large numbers.
The monograph by Athreya and Ney summarizes a common set of conditions under which this law of large numbers is valid. Later there are some improvements through discarding different conditions.
Other branching processes
There are many other branching processes, for example, branching processes in random environments, in which the reproduction law is chosen randomly at each generation, or branching processes, where the growth of the population is controlled by external influences or interacting processes. Branching processes where particles have to work (contribute resources to the environment) in order to be able to reproduce, and live in a changing society structure controlling the distribution of resources, are so-called resource-dependent branching processes. The scaling limit of near-critical branching processes can be used to obtain superprocesses.See also
*Galton–Watson process
The Galton–Watson process, also called the Bienaymé-Galton-Watson process or the Galton-Watson branching process, is a branching stochastic process arising from Francis Galton's statistical investigation of the extinction of family names. The ...
* Random tree
In common usage, randomness is the apparent or actual lack of definite pattern or predictability in information. A random sequence of events, symbols or steps often has no :wikt:order, order and does not follow an intelligible pattern or com ...
* Branching random walk Branching may refer to:
* Branching (linguistics), the general tendency towards a given order of words within sentences and smaller grammatical units within sentences
* Branching (polymer chemistry), the attachment of side chains to a polymer's b ...
* Resource-dependent branching process
* Bruss–Duerinckx theorem
* Martingale (probability theory)
In probability theory, a martingale is a stochastic process in which the expected value of the next observation, given all prior observations, is equal to the most recent value. In other words, the conditional expectation of the next value, given ...
* Superprocess
References
* C. M. Grinstead and J. L. SnellIntroduction to Probability
, 2nd ed. Section 10.3 discusses branching processes in detail together with the application of generating functions to study them. * G. R. Grimmett and D. R. Stirzaker, ''Probability and Random Processes'', 2nd ed., Clarendon Press, Oxford, 1992. Section 5.4 discusses the model of branching processes described above. Section 5.5 discusses a more general model of branching processes known as age-dependent branching processes, in which individuals live for more than one generation. {{DEFAULTSORT:Branching Process Markov processes