Bipolar coordinates on:
[Wikipedia]
[Google]
[Amazon]
 Bipolar coordinates are a two-dimensional
Bipolar coordinates are a two-dimensional 

 The curves of constant ''σ'' correspond to non-concentric circles
:
that intersect at the two foci. The centers of the constant-''σ'' circles lie on the ''y''-axis. Circles of positive ''σ'' are centered above the ''x''-axis, whereas those of negative ''σ'' lie below the axis. As the magnitude , ''σ'', - ''π''/2 decreases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when , ''σ'', = ''π''/2. (From elementary geometry, all triangles on a circle with 2 vertices on opposite ends of a diameter are right triangles.)
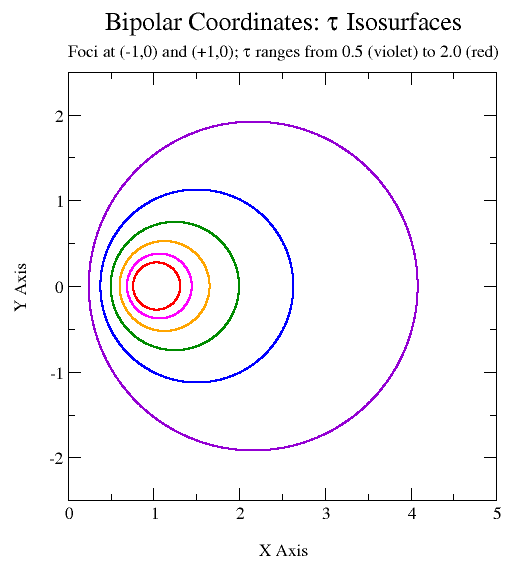
The curves of constant are non-intersecting circles of different radii
:
that surround the foci but again are not concentric. The centers of the constant-''τ'' circles lie on the ''x''-axis. The circles of positive ''τ'' lie in the right-hand side of the plane (''x'' > 0), whereas the circles of negative ''τ'' lie in the left-hand side of the plane (''x'' < 0). The ''τ'' = 0 curve corresponds to the ''y''-axis (''x'' = 0). As the magnitude of ''τ'' increases, the radius of the circles decreases and their centers approach the foci.
The curves of constant ''σ'' correspond to non-concentric circles
:
that intersect at the two foci. The centers of the constant-''σ'' circles lie on the ''y''-axis. Circles of positive ''σ'' are centered above the ''x''-axis, whereas those of negative ''σ'' lie below the axis. As the magnitude , ''σ'', - ''π''/2 decreases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when , ''σ'', = ''π''/2. (From elementary geometry, all triangles on a circle with 2 vertices on opposite ends of a diameter are right triangles.)
The curves of constant are non-intersecting circles of different radii
:
that surround the foci but again are not concentric. The centers of the constant-''τ'' circles lie on the ''x''-axis. The circles of positive ''τ'' lie in the right-hand side of the plane (''x'' > 0), whereas the circles of negative ''τ'' lie in the left-hand side of the plane (''x'' < 0). The ''τ'' = 0 curve corresponds to the ''y''-axis (''x'' = 0). As the magnitude of ''τ'' increases, the radius of the circles decreases and their centers approach the foci.
orthogonal
In mathematics, orthogonality is the generalization of the geometric notion of '' perpendicularity''.
By extension, orthogonality is also used to refer to the separation of specific features of a system. The term also has specialized meanings in ...
coordinate system
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
based on the Apollonian circles
In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. Th ...
.Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, ''Bipolar Coordinates'', CD-ROM edition 1.0, May 20, 1999 Confusingly, the same term is also sometimes used for two-center bipolar coordinates
In mathematics, two-center bipolar coordinates is a coordinate system based on two coordinates which give distances from two fixed centers c_1 and c_2. This system is very useful in some scientific applications (e.g. calculating the electric fie ...
. There is also a third system, based on two poles ( biangular coordinates).
The term "bipolar" is further used on occasion to describe other curves having two singular points (foci), such as ellipse
In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special type of ellipse in ...
s, hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, ca ...
s, and Cassini oval
In geometry, a Cassini oval is a quartic plane curve defined as the locus of points in the plane such that the product of the distances to two fixed points ( foci) is constant. This may be contrasted with an ellipse, for which the ''sum'' of t ...
s. However, the term ''bipolar coordinates'' is reserved for the coordinates described here, and never used for systems associated with those other curves, such as elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal ellipses and hyperbolae. The two foci F_ and F_ are generally taken to be fixed at -a and +a, respectively ...
.

Definition
The system is based on two foci ''F''1 and ''F''2. Referring to the figure at right, the ''σ''-coordinate of a point ''P'' equals the angle ''F''1 ''P'' ''F''2, and the ''τ''-coordinate equals thenatural logarithm
The natural logarithm of a number is its logarithm to the base of the mathematical constant , which is an irrational and transcendental number approximately equal to . The natural logarithm of is generally written as , , or sometimes, if ...
of the ratio of the distances ''d''1 and ''d''2:
:
If, in the Cartesian system, the foci are taken to lie at (−''a'', 0) and (''a'', 0), the coordinates of the point ''P'' are
:
The coordinate ''τ'' ranges from (for points close to ''F''1) to (for points close to ''F''2). The coordinate ''σ'' is only defined modulo ''2π'', and is best taken to range from ''-π'' to ''π'', by taking it as the negative of the acute angle ''F''1 ''P'' ''F''2 if ''P'' is in the lower half plane.
Proof that coordinate system is orthogonal
The equations for ''x'' and ''y'' can be combined to give : This equation shows that ''σ'' and ''τ'' are the real and imaginary parts of an analytic function of ''x+iy'' (with logarithmic branch points at the foci), which in turn proves (by appeal to the general theory ofconformal mapping
In mathematics, a conformal map is a function that locally preserves angles, but not necessarily lengths.
More formally, let U and V be open subsets of \mathbb^n. A function f:U\to V is called conformal (or angle-preserving) at a point u_0\in ...
) (the Cauchy-Riemann equations) that these particular curves of ''σ'' and ''τ'' intersect at right angles, i.e., that the coordinate system is orthogonal.
Curves of constant ''σ'' and ''τ''

 The curves of constant ''σ'' correspond to non-concentric circles
:
that intersect at the two foci. The centers of the constant-''σ'' circles lie on the ''y''-axis. Circles of positive ''σ'' are centered above the ''x''-axis, whereas those of negative ''σ'' lie below the axis. As the magnitude , ''σ'', - ''π''/2 decreases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when , ''σ'', = ''π''/2. (From elementary geometry, all triangles on a circle with 2 vertices on opposite ends of a diameter are right triangles.)
The curves of constant are non-intersecting circles of different radii
:
that surround the foci but again are not concentric. The centers of the constant-''τ'' circles lie on the ''x''-axis. The circles of positive ''τ'' lie in the right-hand side of the plane (''x'' > 0), whereas the circles of negative ''τ'' lie in the left-hand side of the plane (''x'' < 0). The ''τ'' = 0 curve corresponds to the ''y''-axis (''x'' = 0). As the magnitude of ''τ'' increases, the radius of the circles decreases and their centers approach the foci.
The curves of constant ''σ'' correspond to non-concentric circles
:
that intersect at the two foci. The centers of the constant-''σ'' circles lie on the ''y''-axis. Circles of positive ''σ'' are centered above the ''x''-axis, whereas those of negative ''σ'' lie below the axis. As the magnitude , ''σ'', - ''π''/2 decreases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when , ''σ'', = ''π''/2. (From elementary geometry, all triangles on a circle with 2 vertices on opposite ends of a diameter are right triangles.)
The curves of constant are non-intersecting circles of different radii
:
that surround the foci but again are not concentric. The centers of the constant-''τ'' circles lie on the ''x''-axis. The circles of positive ''τ'' lie in the right-hand side of the plane (''x'' > 0), whereas the circles of negative ''τ'' lie in the left-hand side of the plane (''x'' < 0). The ''τ'' = 0 curve corresponds to the ''y''-axis (''x'' = 0). As the magnitude of ''τ'' increases, the radius of the circles decreases and their centers approach the foci.
Reciprocal relations
The passage from the Cartesian coordinates towards the bipolar coordinates can be done via the following formulas: : and : The coordinates also have the identities: : and : which is the limit one would get a x = 0 from the definition in the section above. And all the limits look quite ordinary at x =0.Scale factors
To obtain the scale factors for bipolar coordinates, we take the differential of the equation for , which gives : Multiplying this equation with its complex conjugate yields : Employing the trigonometric identities for products of sines and cosines, we obtain : from which it follows that : Hence the scale factors for ''σ'' and ''τ'' are equal, and given by : Many results now follow in quick succession from the general formulae fororthogonal coordinates In mathematics, orthogonal coordinates are defined as a set of ''d'' coordinates q = (''q''1, ''q''2, ..., ''q'd'') in which the coordinate hypersurfaces all meet at right angles (note: superscripts are indices, not exponents). A coordinate su ...
.
Thus, the infinitesimal area element equals
:
and the Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is the ...
is given by
:
Expressions for , , and can be expressed obtained by substituting the scale factors into the general formulae found in orthogonal coordinates In mathematics, orthogonal coordinates are defined as a set of ''d'' coordinates q = (''q''1, ''q''2, ..., ''q'd'') in which the coordinate hypersurfaces all meet at right angles (note: superscripts are indices, not exponents). A coordinate su ...
.
Applications
The classic applications of bipolar coordinates are in solvingpartial differential equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.
The function is often thought of as an "unknown" to be solved for, similarly to ...
, e.g., Laplace's equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as
\nabla^2\! f = 0 or \Delta f = 0,
where \Delta = \na ...
or the Helmholtz equation
In mathematics, the eigenvalue problem for the Laplace operator is known as the Helmholtz equation. It corresponds to the linear partial differential equation
\nabla^2 f = -k^2 f,
where is the Laplace operator (or "Laplacian"), is the eigenvalu ...
, for which bipolar coordinates allow a separation of variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs ...
. An example is the electric field
An electric field (sometimes E-field) is the physical field that surrounds electrically charged particles and exerts force on all other charged particles in the field, either attracting or repelling them. It also refers to the physical field ...
surrounding two parallel cylindrical conductors with unequal diameters.
Polar plotters use bipolar coordinates to describe the drawing paths required to draw a target image.
Extension to 3-dimensions
Bipolar coordinates form the basis for several sets of three-dimensionalorthogonal coordinates In mathematics, orthogonal coordinates are defined as a set of ''d'' coordinates q = (''q''1, ''q''2, ..., ''q'd'') in which the coordinate hypersurfaces all meet at right angles (note: superscripts are indices, not exponents). A coordinate su ...
.
*The bipolar cylindrical coordinates are produced by translating the bipolar coordinates along the ''z''-axis, i.e., the out-of-plane axis.
*The bispherical coordinates are produced by rotating the bipolar coordinates about the ''x''-axis, i.e., the axis connecting the foci.
*The toroidal coordinates
Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci F_1 and F_2 in bipolar coordina ...
are produced by rotating the bipolar coordinates about the ''y''-axis, i.e., the axis separating the foci.
References
* * Korn GA and Korn TM. (1961) ''Mathematical Handbook for Scientists and Engineers'', McGraw-Hill. {{Orthogonal coordinate systems Two-dimensional coordinate systems Orthogonal coordinate systems